基于滑模变结构永磁同步电机速度控制器

王 斌，丁 强

（南京工业职业技术学院 电气与电子工程学院，南京 210046）

0 引言

永磁同步电动机具有小体积、高效率、高功率因数、小转动惯量、高速响应性能和在矢量控制情况下控制简单等优点，使其在低速或直接驱动场合发挥重要作用。同时它又是非线性、多变量、强耦合、时变的系统，只有选用合适的控制策略，才能发挥其较好机械性能。电机运行中的绕组升温等因素，绕组参数会发生不同程度的摄动。电机的转动惯量和负载转矩大多不精确，甚至是未知的。克服参数变化和不确定因素的影响，实现电机高性能控制是具有实际意义的。

传统PI控制在永磁同步电动机矢量控制中被广泛应用，但由于算法本身对电机本体参数的依赖，使得其鲁棒性较差。自适应控制、神经网络控制因算法本身复杂，计算量大，所以其控制优势也不明显。

近年来，滑模变结构控制受到越来越多重视。滑模变结构控制是调整反馈控制系统的结构，使它的状态向量通过开关平面时发生变化，系统的状态向量被约束在开关面的领域内滑动。系统的动态品质由开关面的参数决定，与系统的参数、扰动无关，具有很好的鲁棒控制性。适用于永磁同步电动机这类被控对象。

本文在两轴旋转坐标系下设计了一种面装式永磁同步电动机滑模变结构PI速度控制器，仿真验证该控制器的有效性。

1 PMSM数学模型

选择电机的直轴、交轴电流及机械角速度为状态变量，可以得到面装式永磁同步电机的状态方程：

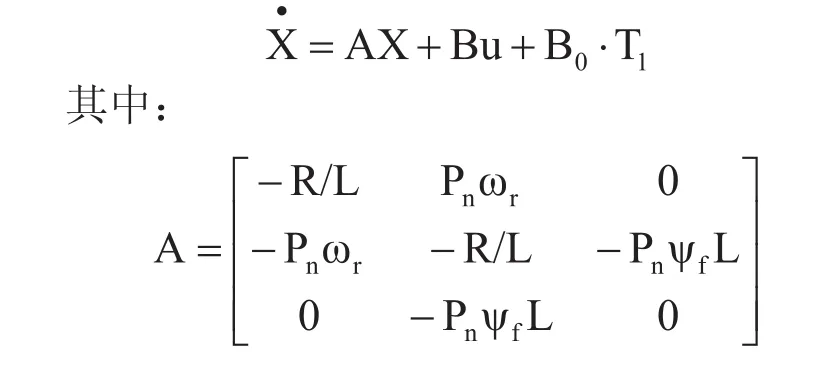
R、L为定子电阻和电感；Pn为极对数；ωr为机械角速度；Ψf为永磁磁链；J为转动惯量；ud、uq为dq轴定子电压；id、iq为dq轴定子电流。

2 滑模变结构基本原理

滑模变结构控制是一种高速切换反馈控制，控制律和闭环系统的结构在滑模面上不连续，通过设计把不同结构下的相轨迹拓扑的优点结合起来，实现预期设计的性能。由于滑模面一般是固定的，系统对于参数变化和外部扰动不敏感，具有较强鲁棒性。

设二阶系统状态可用如下状态方程描述：

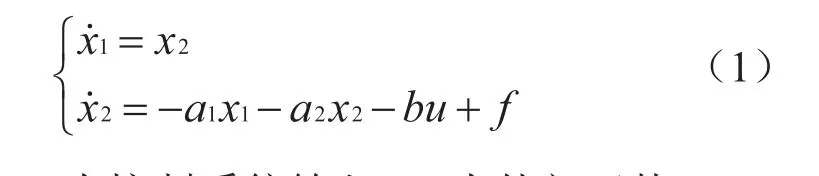
其中：u为控制系统输入，f为外部干扰，x1、x2为状态变量，a1、a2、b为常参数或时变参数，其精确值可以未知，但其变化范围为：

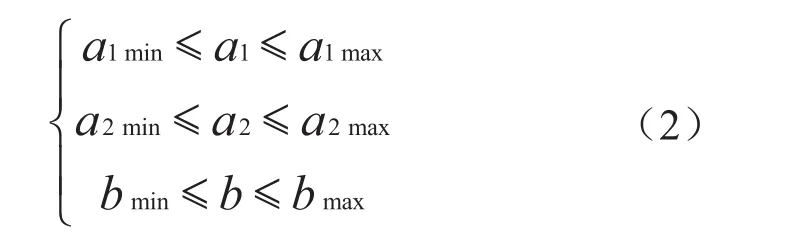
定义滑模切换函数为s＝cx1＋x2。直线s＝0为切换线，在这个切换线上控制u是不连续的，其表达式为：

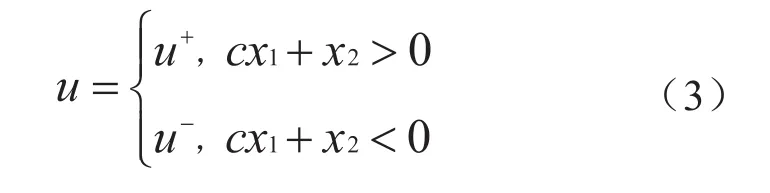
其中u+≠u-，c＞0。

为形成滑动，切换线两侧必须满足条件：

由式(3)、(4)可得：

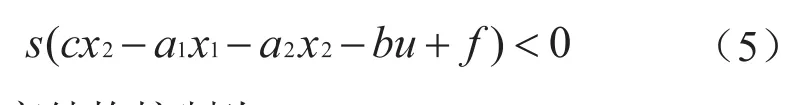
选取变结构控制为：

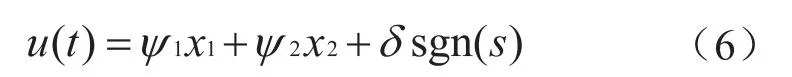
其中：

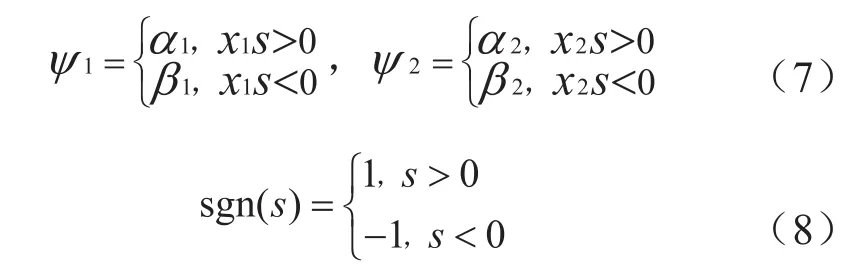
由式(5)、(6)可得：

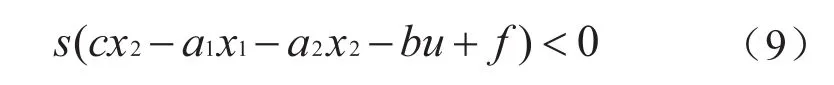
因此二阶系统变结构调节器参数为：

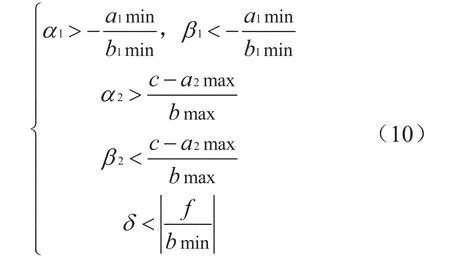
3 滑模PI速度控制器设计

采用id＝0的矢量控制方式时PMSM的解耦状态方程为：

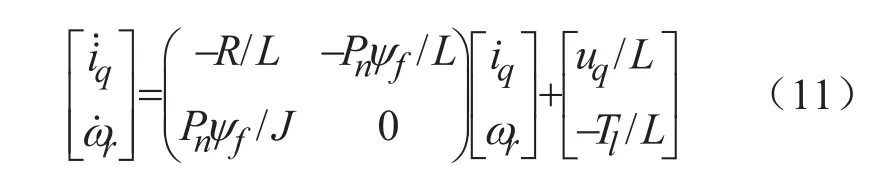
令状态量x1＝ωref－ωfdb代表速度误差，x2＝1作为速度滑模调节器输入，调节器输出即电流给定u＝iqref，从而得到系统在相空间上的数学模型为：

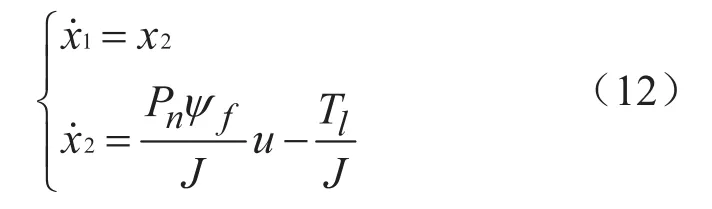
在考虑系统转速受限的情况下，取滑模切换函数为：s＝cx1－x2，其中c＞0为常数。令滑模变结构调节器的输出为：

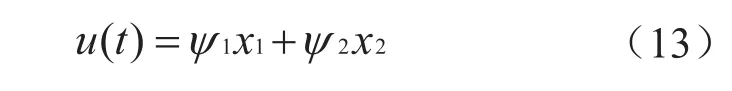
其中：

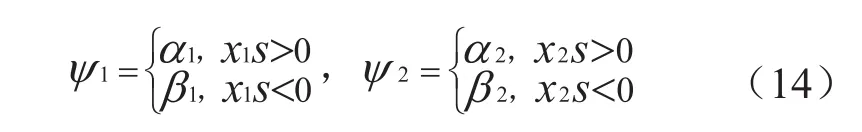
由式(10)代入状态方程中的相关系数，可以得到速度环滑模变结构调节器参数：

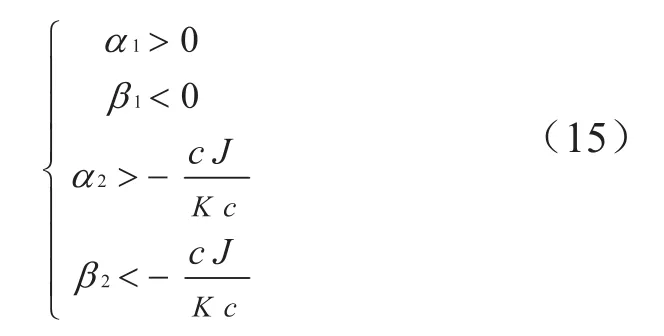
永磁同步电动机滑模变结构PI速度控制策略系统框图如图1所示。

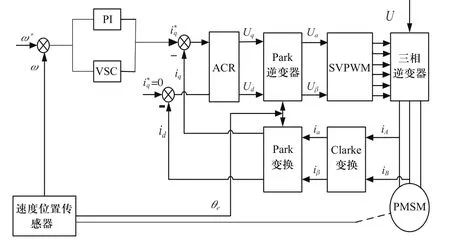
图1 滑模变结构PI控制系统框图

4 仿真实验

本文为验证滑模变结构PI速度控制器有效性，进行额定转速阶跃仿真实验，并与传统PI速度控制器进行对比。仿真实验电机主要参数为：额定功率1.5kW；额定转速1500 r/min；转动惯量8.2 kg ·cm2；极对数2对极；额定电压220V；额定电流6A；Ld＝Lq＝2mH。

图2为给定转速为额定转速时，滑模变结构PI速度控制器和传统PI速度控制器控制效果对比波形。

图2可以看出，与传统PI速度控制器相比，滑模变结构PI速度控制器作用时速度超调变小，系统稳定快。

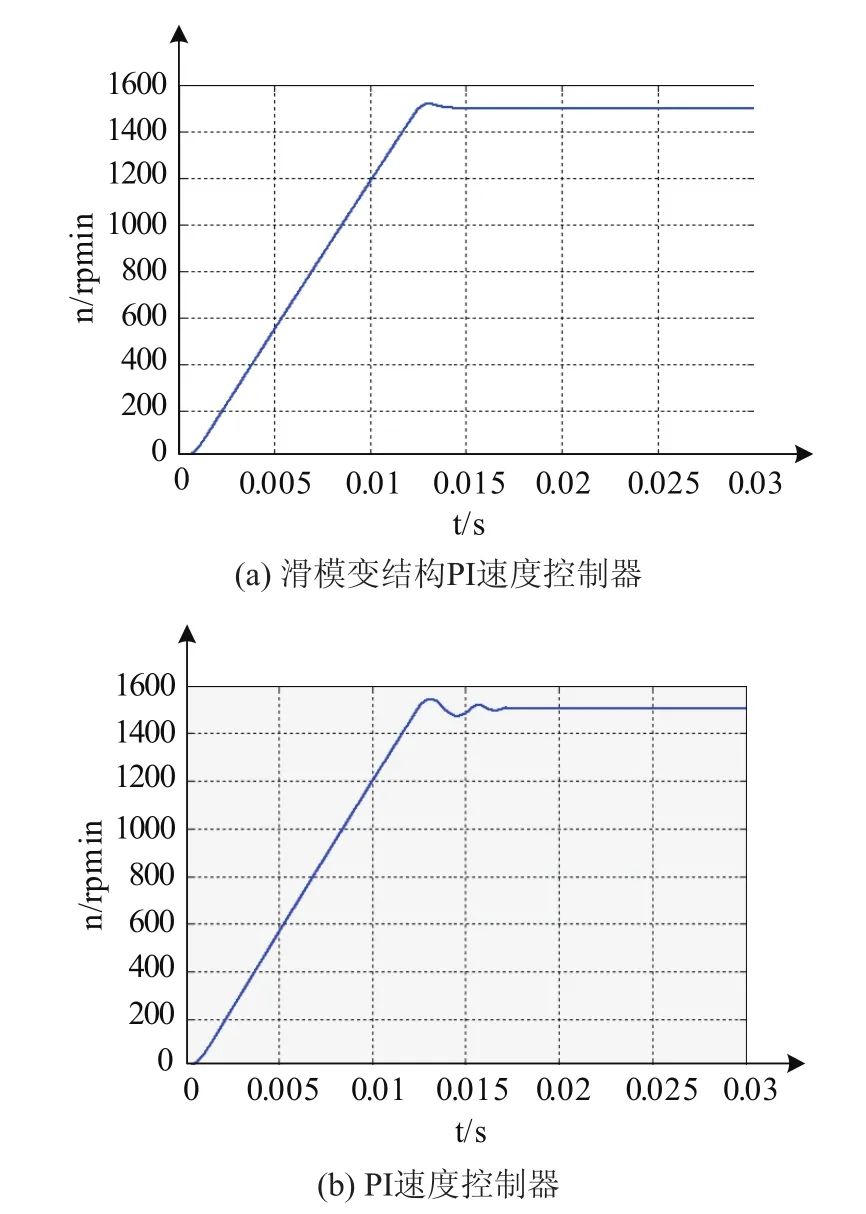
图2 速度阶跃控制效果对比

5 结论

本文设计了永磁同步电动机滑模变结构PI速度控制器，来改善电机速度性能，抑制速度阶跃响应的超调，提高系统动态响应和抗扰能力。通过仿真实验并与传统PI速度控制器相比较，证明了该速度控制策略的可行性，为提高永磁同步电动机速度控制性能奠定基础。

[1].金如麟, 谭弗娃.永磁同步电动机的应用前景[J].上海大中型电机, 2001, 14(5): 9-13.

[2].郭庆鼎, 王成元.交流伺服系统[M].北京: 机械工业出版社, 1994.

[3].V.I.Utkin.Sliding mode control design principles and applications to electric drives[J].IEEE Trans.on IE, 1993,40(2): 23-36.

[4].Barret Steel, Lyndon Stephens.A Test Rig for Measuring Force and Torque Production in a Lorenz, Slotless Self Bearing Motor[C].ISMB, August 23-25, 2000, ETH Zurich: 407-412.

[5].赵德宗, 张承进, 郝兰英.一种无速度传感器感应电机鲁棒滑模控制策略[J].中国电机工程学报, 2006, 26(12):123-127.

[6].王瑞明, 蒋静坪.基于适应性遗传算法的滑模控制感应电机伺服驱动系统研究[J].中国电机工程学报, 2005,25(11): 137-141.

[7].Cheng K, Tzou Y.Fuzzy optimization techniques applied to the design of a digital PMSM servo drive[J].IEEE Transactions on Power Electronics, 2004, 19(4):1085-1099.

[8].田艳丰, 郭庆鼎.永磁直线同步电动机的滑模-H_∞鲁棒跟踪控制[J].电工技术学报, 2004, 19(7): 2-5.