非线性广义模糊系统的镇定控制器设计与分析

刘 伟，路子赟

（江苏技术师范学院，常州 213001）

0 引言

镇定和跟踪是控制的两个主要方面。跟踪控制，尤其是状态跟踪控制更具有十分重要的研究价值。首先，系统动态性能不完全由极点决定，也不依赖于零点，但目前零点配置未完全解决。其次，有些情况下，系统参数不确定或者在运行时有一定的飘移，都会使闭环系统的特性变坏，甚至不稳定而无法工作。由一个理想模型给出希望的动态特性，并设计状态跟踪器常常可以解决上述问题。T-S模糊系统自提出以来就引起了国内外控制领域的普遍重视，许多学者对T-S模糊系统的稳定性进行了研究，并得到了许多关于系统稳定性的结果[1～7]。然而，这些结果大部分都是利用公共Lyapunov函数方法得到的关于T-S模糊系统二次稳定的充分性条件。由于模糊系统本质上是非线性系统，因此用单一的Lyapunov函数分析系统的稳定性必定存在着很大的保守性。针对这一问题，最近，Tanaka等[8～10]对连续模糊系统提出了模糊Lyapunov函数方法，对隶属函数的导数给出限制，得到了系统稳定的充分条件，文献[9]给出了控制器设计方法。但文献[9]中给出了控制器的设计方法不是LMI的，计算量也很大，因此在应用上存在很大的局限性。

本文针对这一问题，将广义系统方法和模糊Lyapunov函数方法结合，既克服了单一的Lyapunov函数方法保守性较大的缺点，又解决了模糊Lyapunov函数方法计算量过大和难以得到LMI形式结果的问题。给出了基于LMI的PDC控制器设计方法。而且，放松了对隶属函数导数的限制条件。

1 T-S模糊系统

考虑如下T-S模糊系统

其中： 是状态向量， 是控制输入，Ai，Bi是维数适当的常数矩

系统（1）的自治系统为

为了分析系统（2）的稳定性，文献[9]引入如下假设条件：

假设1[9]

利用如下形式模糊Lyapunov函数

引理1[9]如果存在常数 ，使假设1成立，且存在矩阵 满足下面的LMIs：

那么模糊系统（2）是稳定的。

对于引理1，显然， 越小越容易得到可行解，假设1决定了 ，而且都有限制，在此对假设1进行了放松，给出如下假设：

假设2

利用文献[11]中的广义系统方法，将系统（1）改写为如下模糊广义系统形式。

系统（2）可改写为

考虑广义模糊Lyapunov函数

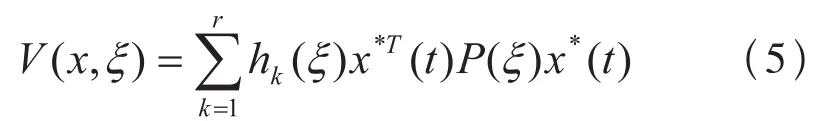
其中

利用广义Lyapunov函数（5）给出如下定理：

定理1 如果存在常数ϕ1, ϕ2, , ϕr使假设2成立，且存在矩阵P1i(i＝1, 2, , r), P2, P3使下面的LMIs

成立，其中：

那么模糊系统（2）是稳定的。

证明：对式（5）给出的Lyapunov函数求导，根据式（4），假设2和 可得

系统（2）的稳定性得证。 证毕。

与式（3）中的模糊Lyapunov函数相比，式（5）给出的广义模糊Lyapunov函数引入了松弛变量P2和P3，利用它来分析原T-S模糊系统的稳定性，所得结果LMI个数比引理1少，更重要的是P2k和Ai没有相乘的关系，这样可以得到基于LMI的PDC控制器设计方法。

在hi(ξ)满足如下假设的时候，可以将定理1进一步化简。

假设3[11]

其中vk，k＝1, 2, , r是常数。

定理2[11]如果存在常数v1, v2, , vr使假设3成立，且存在矩阵P1i，i＝1, 2, , r, P2, P3使下面的LMIs

成立，其中Q2i, Q3与定理1中相同，那么模糊系统（2）是稳定的。

2 模糊系统的控制器设计

以上给出了T-S模糊系统稳定性的判别条件，下面将讨论T-S模糊系统的镇定控制器设计方法。考虑PDC控制器

将控制器（6）代入系统（1）得闭环系统

对应的广义模糊系统为

定理 3 如果存在常数ϕ1, ϕ2, …, ϕϕ，使假设 2成立，且存在矩阵P1i(i＝1, 2, …, r), P2, P3满足下面的不等式：

其中：

那么模糊系统（7）是稳定的。

证明：对式（5）给出的Lyapunov函数求导，根据式（8）和假设2可得

闭环系统（7）的稳定性得证。证毕。

下面给出基于LMI的PDC控制器设计方法。

定理 4 如果存在常数ϕ1, ϕ2, …, ϕr使假设 2 成立，且存在矩阵X1i, Mi, i＝1, 2, …, r, X2满足下面的LMIs：

其中：

证明：对式（9）取P3＝P2左右分别乘

下面，考虑模糊系统隶属函数性质，对定理4的条件进一步放松。由这一性质，那么可以得到如下定理：

其中：

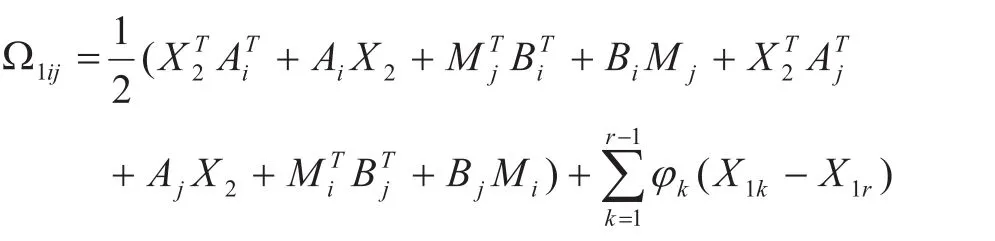
那么模糊系统（7）是稳定的，且

3 例子

通过这个例子来证明本文给出方法的有效性。关系式如下：

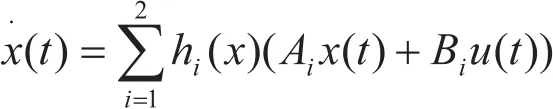
其中：

将K11, K21代入原系统，闭环系统的起始状态为[0.5 -1]T时的状态响应如图1所示。

图1 闭环系统状态响应

4 结论

本文应用广义模糊Lyapunov方法研究了T-S模糊系统的稳定性分析与镇定控制器设计问题。即克服了单一Lyapunov函数方法保守性较大的缺点，又解决了模糊Lyapunov函数方法计算量较大和难以得到LMI形式结果的问题。最后的例子验证了方法的优越性和有效性。

[1] KIME, LEEH. New approaches to relaxed quadratic stability condition of fuzzy control systems[j]. IEEE Trans on Fuzzy systems, 2000, 8(5): 523-533.

[2] CAO G, REE W, FENG G.Control of nonlinear continuous time systems based on dynamical fuzzy models[J]. Int J of Systems Science, 1996, 27(9): 821-830.

[3] ZHANG J M, LI R H,ZHANG P A.Stability analysis and systems design of fuzzy control systems[J].Fuzzy Sets and Systems, 2001, 120(1): 65-72.

[4] TAKAGI T, SUGENO M. Fuzzy identification of systems and its applications to modeling and control[J]. IEEE Trans on Systems Man, and Cybernetics,1985, 15(1): 116-132.

[5] Tseng C S, Chen B S,U H L, fuzzy control systems design for nonlinear dynamic systems T-S fuzzy model. IEEE Transactions on Fuzzy Systems, 2001, 9(3): 381-392

[6] TANAKA K, SUGENO M.Stability analysis and design of fuzzy control systems[J].Fuzzy Sets and Systems, 1992,45(2): 135-156.

[7] LIU X D, ZHANG Q L.Approaches to quadratic stability conditions and control designs for T-S fuzzy systems[J].IEEE Trans on fuzzy Systems, 2003, 11(6): 830-839.

[8] LIU X D,ZHANG Q L. New approaches to controller designs based on fuzzy observers for T-S fuzzy systems via LMI[J]. Automatica, 2003, 39(9): 1571-1582.

[9] TANAKA K, HORI K, WANG H O. A multiple Lyapunov function approach to stabilization of fuzzy control systems[J].IEEE Trans on Fuzzy Systems, 2003, 11(4). 582-589.

[10] TANAKA K, HORI T, WANG H O.A fuzzy Lyapunov approach to fuzzy control systems design[C]. Proc of American Control Conference.Arlington, VA, USA: IEEE Press, 2001: 4790-4795.

[11] CHADLI M, MAQUIN D, RAGOT J.Relaxed stability conditions for Takagi-Sugeno fuzzy systems[C]. Proc of IEEE Conf on Systems Man and Cybernetics. Nashville,USA: IEEE Press, 2000: 3514-3519.