基于OFDM定时捕获的分布式天线位置设计*

卿朝进，夏 天，唐友喜，查光明

(电子科技大学 通信抗干扰技术国家重点实验室,四川 成都 611731)

正交频分复用OFDM(Orthogonal Frequency Division Multiplexing)技术能很好地对抗频率选择性衰落，因而被广泛应用于诸如无线局域网、数字广播电视等无线通信系统中[1]。与此同时，分布式天线系统DAS(Distributed Antenna Systems)具有诸如增加系统的覆盖、提高系统频谱效率等优点，是第四代移动通信的关键技术之一[2]。分布式天线与OFDM技术的结合，将是一项很有前瞻性的课题。

然而，分布式天线的位置部署，直接影响着分布式天线系统优点的实现[3-5]。通过最小化区域平均误码率，参考文献[3]研究了线形小区中，两根分布式天线的位置设计。参考文献[4]将参考文献[3]的工作扩展到圆形小区，通过最大化小区平均容量进行天线位置设计。类似于参考文献[3]的最小化区域平均误码率方法，参考文献 [5]在圆形小区中进行多根分布式天线位置部署。然而，这些方法均是在时间和频率理想同步的情况下提出的。事实上，系统同步性能的好坏严重影响着系统的整体性能。在系统没有同步的情况下，参考文献[3-5]的天线位置设计方法也无从谈起。

为此，本文在考虑OFDM同步性能影响的情况下，进行天线位置设计。由于定时捕获是同步过程的首要环节，为方便起见，本文研究基于OFDM定时捕获的分布式天线位置设计。根据最小最大准则[6]，首先利用各分布式接收天线的正确检测概率，推导出最坏捕获情况发生的概率(表示为PWC)。然后再遍历两分布式天线所有可取位置组合，最小化PWC，从而得到两分布式天线的最优位置。仿真表明，当移动台位置在线形小区中均匀分布时，两分布式接收天线应根据线形小区中心对称放置。

1 系统模型

线形小区如图1所示，线形小区的长度为R，基站两分布式天线DRX1和DRX2的位置分别为a1和 a2,移动台(MS)的位置为 x。经过 IFFT变换后，OFDM发射信号的基带形式为:

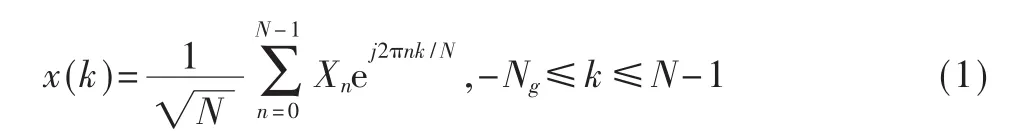
其中,Xn表示调制到第n个子载波上独立同分布的数据序列；Ng为循环前缀长度；发射信号功率为

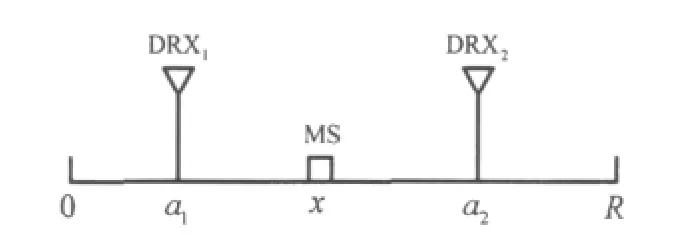
图1 线形小区示意图

DRXi(i=1,2)处的接收信号为:

其中,τi和εi分别为 MS与DRXi间的定时偏移和归一化的载波频偏，wi(k)为零均值的复高斯白噪声，其方差为表示小尺度多径数量，hi(m)为第m条径的信道冲击响应。根据参考文献[4]，式(2)中的c为常数，si表示阴影衰落，α为路径损耗因子，Di表示MS与DRXi间有效距离。

2 天线位置设计

本文着重于分布式天线的位置设计，训练序列结构不是本文的研究重点,为此,本文的训练序列[s(0),…,s(N-1)采用3GPP-LET标准推荐的自相关特性良好的CHU序列[7]。对于预定的虚警概率，自相关定时捕获方法[1]的检测门限没有闭式解[8]，为方便起见，本文采用基于检测门限的互相关定时捕获方法[9]进行OFDM的定时捕获(注，天线位置设计也可采用自相关定时捕获方法，其门限可根据数值计算求得[8]，这里将研究重心放在天线位置设计上，采用方便门限计算的互相关定时捕获方法)。接收信号与训练序列间的互相关系为：

其中，m∈[0,U-N]，U为观测矢量的长度，假设 U足够长，可以在接收信号中观测到整个的训练序列。定时偏移 τi的估计值可表示为[1]:

其中，λ根据FFT窗的开始点不被信道弥散影响进行选择[10](参考文献[9]将 λ选择为循环前缀长度 Ng的一半)。 根据式(3)，取

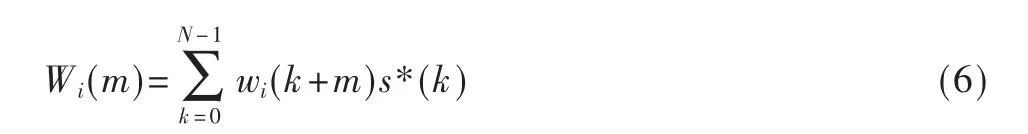
其中，Wi(m)为零均值的高斯噪声，其方差为对于给定的虚警概率PFA(假设 DRX1和DRX2处的虚警要求相同)，根据参考文献[9]，可以得到 DRXi的检测门限为:

利用检测门限 γi，在 m∈[0,U-N]上，当最大的超过门限时，根据式(5)可完成粗定时同步(定时捕获)。

用PDi表示DRXi的正确检测概率，有:

对于所研究的线形小区,期望最坏捕获情况最小化(即最不愿意看到两根分布式接收天线均不能完成对移动台的定时捕获，这样，该小区便不能为该移动台服务)。取 PN为 DRX1和 DRX2均不能正确检测(漏检或检测错误)的概率，于是有:

这里将正确检测概率PDi表示为|x-ai|的函数，其中，|xai|表示 MS到DRXi的距离。当 MS处于某一特定位置时，最坏情况在PN达到最大值时发生，从而，最坏情况的概率PWC可表示为:

其中,p(x)为MS出现位置的概率密度函数。为获得最佳的性能，PWC应尽可能地小。从而，天线位置设计问题转化为最小最大估计问题[6]。根据参考文献[6]，最优天线位置可取为：

根据式(10)和式(11)有:

不失一般性，可假设MS的位置x在[0,R]上服从均匀分布，也即是:

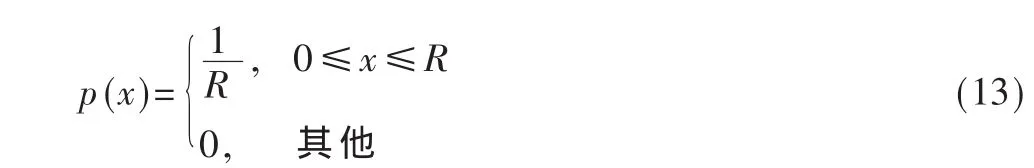
对于 x∈[0,R]，p(x)为一常数。 于是，式(12)等价于

根据式(14)，可以得到最小最大准则下 DRX1和 DRX2的最优位置。

3 数值仿真

根据参考文献[1]取 N=128，Ng=16，PFA=10-6；由参考文献[4]，取 c·100-3.7=-78 dB，α=3.7，阴影的标准偏差为8 dB；取载波频率为 2 GHz，采样频率为10 MHz，MS与DRXi间的相对运动速度为120 km/h，最大多普勒频移为222.2 Hz，多径信道模型为参考文献[11]中的 Vehicular-A信道。不失一般性，假设由参考文献[12],对于给定距离D,接收机平均输入信噪比中值ρ为：

取ρ=5 dB，图2给出了最坏情况概率 PWC与两分布式天线的位置的关系，其中，搜索步长为5 m。根据图2的仿真，DRX1和DRX2的位置分别为a1=170 m和a2=830 m，DRX1和DRX2相对于线形小区中心对称。

图2 最坏情况概率PWC与两天线位置的关系

考虑两分布式接收天线位置的所有组合，图3给出了最坏情况发生的次数与移动台位置的关系。从图3可以看出，最坏情况主要发生在线形小区的边界，其次是小区中心位置附近。

基于OFDM定时捕获，本文研究了两分布式天线在线形小区中的位置设计。根据最小最大准则，在两分布式天线的所有位置组合中，最小化最坏捕获情况的概率，从而得到两分布式接收天线的最优位置。当移动台位置均匀分布于线形小区时，仿真结果表明，天线位置应根据小区中心对称放置。本文只考虑了两根分布式天线和线形小区，该方法可被扩展到多根分布式天线和其他小区模型中。

图3 最坏情况发生的次数与移动台位置的关系

[1]MORELLI M,KUO C C,PUN M O.Synchronization techniques for orthogonal frequency division multiple access(OFDMA):a tutorial review[J].Proc.IEEE,2007,95(7):1394-1427.

[2]CASTANHEIRA D,GAMEIRO A.Distributed antenna system capacity scaling[J].IEEE Wireless Commun.,2010,17(3):68-75.

[3]SHEN Y,TANG Y,KONG T,et al.Optimal antenna location for STBC-OFDM downlink with distributed transmit antennas in linear cells.IEEE Commun.Lett.,2007,11:387-389.

[4]WANG X,ZHU P,CHEN M.Antenna location design for generalized distributed antenna systems.IEEE Commun.Lett.,2009,13:315-317.

[5]HAN L,TANG Y,SHAO S,et al.On the design of antenna location for OSTBC with distributed transmit antennas in a circular cell.in Proc.IEEE International Conference on Communications(ICC),Cape Town,South Africa,2010:1-5.

[6]VERDU S,POOR H.On minimax robustness:a general approach and applications[J].IEEE Trans.Inf.Theory,1984,30(2):328-340.

[7]3GPP,TS 36.221,3rd Generation Partnership Project;Technical Specification Group Radio Access Network;Evolved Universal Terrestrial Radio Access(E-UTRA);Physical Channels and Modulation(Release 8),v.8.7.0,May 2009.

[8]SHI K,SERPEDIN E.Coarse frame and carrier synchronization of OFDM systems:a new metric and comparison[J].IEEE Trans.Wireless Commun.,2004,3(4):1271-1284.

[9]AWOSEYILA A,KASPARIS C,EVANS B.Robust timedomain timing and frequency synchronization for OFDM systems[J].IEEE Trans.Consum.Electron.,2009,55(2):391-399.

[10]MINN H,BHARGAVA V,LETAIEF K.A robust timing and frequency synchronization for OFDM systems[J].IEEE Trans.Wireless Commun.,2003,2(4):822-839.

[11]ITU-R M.1225.Guidelines for evaluation of radio transmission technologies for IMT-2000.Recommendation ITUR M 1225,1997.

[12]CATREUX S,DRIESSEN P,GREENSTEIN L.Data throughputs using multiple-input multiple-output(MIMO)techniques in a noise-limited cellular environment[J].IEEE Trans.Wireless Commun.,2002,1(2):226-235.