SPWM逆变器死区问题研究

王明渝，王 磊，安树怀，俞 鹏

（重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044）

三相桥式逆变电路中，通常采用双极性SPWM调制技术。任何固态的功率开关管都存在着一定的导通和关断时间,为确保同一桥臂上下开关管不致发生直通故障，通常采用将理想的SPWM驱动信号上升沿(或下降沿)延迟一段时间Td(称为死区时间)[1]。死区是为保证开关器件安全、可靠运行而采取的措施。

针对死区带来的死区效应，很多学者进行了大量研究[1-5]。参考文献[1]通过建立数学模型进行定量计算，对死区引起的输出电压基波，低次谐波的变化规律进行了分析。较低的总谐波畸变率(THD)与较快的动态响应是逆变电路所期望达到的指标，因此对死区带来的谐波影响应该引起更高的关注。参考文献[6]在建立 SPWM学模型的基础上，分析了不同模式下SPWM电压源型逆变器的谐波和载波比以及与调制深度的关系。参考文献[2]通过数学模型和仿真分析了死区对逆变器输出电压和产生附加谐波的影响，进而对电动机负载中磁链矢量偏移和附加损耗方面进行了讨论，其重点在附加损耗方面。上述虽然都针对死区对输出电压的影响进行了分析，但系统性不够完善。

理论上SPWM逆变器输出电压中的谐波分量应该聚集在以开关频率及其倍频数为中心的一定范围，当此谐波被LC滤波器滤除后,输出电压失真度应相当小,且严格正比于调制比的正弦波形。但在实际应用中，由于死区时间的设置和开关器件固有特性(通态电压降和开关时间)的影响，带来的低次谐波给输出电压造成了严重的波形畸变和基波电压损失,从而使系统的动、静态性能下降，增加了低次谐波抑制的难度，降低了高速开关器件的实际应用效果。

本文通过仿真分析了死区时间对逆变器产生的谐波影响，提出了通过死区补偿改善波形质量的必要性及有益于逆变器设计的结论。

1 死区效应分析

本文采用三相全桥SPWM逆变电路结构如图1所示。调制方式采用双极性调制,逆变器采用对称方式注入死区时间。

设由逆变器流向负载的方向为输出电流ia的正方向。在死区时间内，同一桥臂的两个开关管均处于关断状态，输出电流只能通过二极管续流，桥臂的输出电压与输出电流的极性有关，而与驱动信号的控制逻辑无关。以桥臂A为例进行分析,在死区时间Td内，当电流流出桥臂(ia＞0)时，由二极管 D4续流，将输出电压 VAN钳位在负母线电压-E/2；反之，当电流流入桥臂(ia＜0)时，由二极管D1续流，将输出电压VAN钳位在正母线电压E/2。如图2所示，实际输出电压与理想输出电压相比较出现了一个误差电压Ve。由图2(d)可以看出误差电压Ve具有的特征：(1)在每个开关周期内均存在一个误差电压脉冲；(2)每个脉冲的幅值均为E；(3)每个脉冲的宽度均为Td；(4)每个脉冲的极性与输出电流ia的极性相反。

图1 三相逆变器电路

图2 死区对逆变器输出电压的影响

2 死区对基波的影响

[1]推导出死区对基波的影响：通过对不含死区时间的理想波与加入死区时间的实际波之间的对比，得到输出基波幅值随调制深度M的减小而减小；当开关频率f增加时，基波电压下降的速度增大；功率因数角φ越小，基波电压下降越多；基波电压随死区时间Td的增加直线下降。

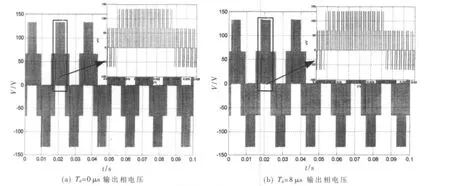
图3 输出相电压对比

3 死区引起的附加谐波

死区还会对输出电压的谐波产生影响。由于谐波的存在，不仅造成功率因数降低，影响效率，而且还可能引起逆变器自身以及其他设备的共振，同时造成电机低速转矩脉动。通常可用LC滤波器消除谐波，但因为LC滤波器是按照滤除开关频率谐波而设计的，随着开关频率不断提高，频率调制比也随之不断提高，使得由死区引入的3、5、7等低次谐波无法得到有效衰减，从而给输出电压造成了严重的波形畸变。

本文利用总谐波畸变率 (THD)研究死区带来的谐波影响。首先对SPWM输出电压进行谐波分析，对SPWM逆变电源作以下假设：(1)直流电压E是最理想的电压源，可不考虑其纹波对逆变器输出的影响；(2)开关器件为理想器件，具有理想的开关特性；(3)逆变器采用双极性SPWM调制，三角波频率fc与逆变器输出电压频率f之比N>1，正弦调制波的幅值与载波幅值之比M≤1。

SPWM输出相电压傅里叶分解得：

由式(1)的第二项得出逆变电源输出电压一部分谐波分量的频率为载波频率的奇数倍。由式(1)的第三项得出逆变电源输出电压的另一部分谐波分量对称分布在整数倍的载波频率周围，其频率可表示为mω+nω，m是相对于载波的谐波次数，n是相对于调制波的谐波次数。

理想情况下，输出电压谐波中应不含低次谐波。但实际电路中的谐波含量比理想情况下的含量要多，同时也会出现少量的低次谐波。

图3(a)、(b)分别为 M=0.5，N=41，φ=45°时，Td=0 μs、Td=8 μs情况下的输出相电压的波形。进行fourier分析，可以得到其THD分别为26.67%、44.38%。对其第一边带的低次谐波进行fourier分析,可得其THD分别为2.41%和 20.04%，如图4所示。 对比图4(a)、图4(b)的fourier分析可以看到死区时间的加入带来了3、5、7…低次谐波。

下面对死区带来的谐波影响进行分析：

参考文献[2]在一个基波周期内把N个由Td引起的正负脉冲等效成一定高度的矩形波Ve，则其傅里叶展开式为：

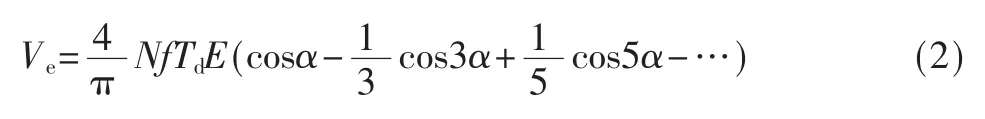
若忽略PWM调制波固有的谐波含量，而只考虑死区时间对基波电压的影响，则可得:

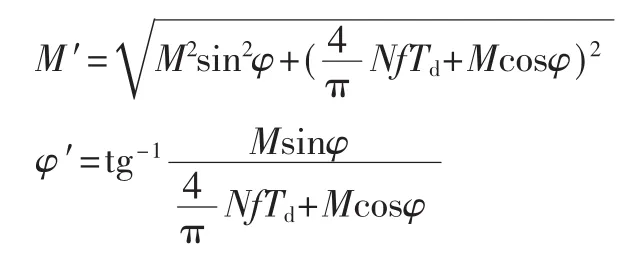
从而基波幅值为：

谐波幅值为:

式中,ΔTHD为忽略 PWM调制波固有的谐波含量，而只考虑死区时间对基波电压的总谐波畸变率。由式(7)可以看出,死区对输出电压带来的谐波总畸变率ΔTHD与调制深度M、开关频率 f、功率因数角 φ及死区时间Td之间的关系。进行仿真可得到其变化规律曲线如图5所示 (仿真中只针对第一边带内的低次谐波进行ΔTHD测量)。对图5 ΔTHD变化规律分析如下：

图5(a)曲线 1、2、3 分别为 ΔTHD 在 M=0.5，N=120，T=0.02 s，φ=30°、45°、60°时随死区时间 Td的变化规律。总谐波畸变率ΔTHD随死区时间的增大而成直线上升，死区时间越大，畸变率越高。同时由曲线1、2、3的对比可以看到功率因数越低(即功率因数角越大)，畸变率越大。图中虚线4为由式(7)计算所得的理论值（下同）。

图5(b) 曲线 1、2、3分别为 ΔTHD 在 M=0.7、0.5、0.3,φ=45°，Td=4 μs时随频率调制比 N 的变化规律，当输出频率不变，开关频率增加时，ΔTHD增加。图中虚线4为M=0.5时的理论计算曲线。

图5(c)曲线 1、2、3 分别为 ΔTHD 在 N=120，T=0.02s，Td=4 μs，φ=60°、45°、30°时随调制深度 M 的变化规 律。由曲线图可得在相同的功率因数下,ΔTHD随M的增大而减小，即调制比越大，畸变率越小。图中虚线4为φ=45°的理论计算曲线。

由图5(a)、(c)可看出ΔTHD与功率因数之间的关系，功率因数越大(功率因数角越小)，畸变率ΔTHD的值越小。图5(d)曲线 1、2、3分别是 ΔTHD 在 M=0.7、0.5、0.3,Td=4 μs，N=120，T=0.02 s 时随功率因数的变化规律。由此可以看到，随功率因数角的增大(即功率因数的减小)，ΔTHD的值也增大，图中虚线4为 M=0.5时的理论计算曲线。

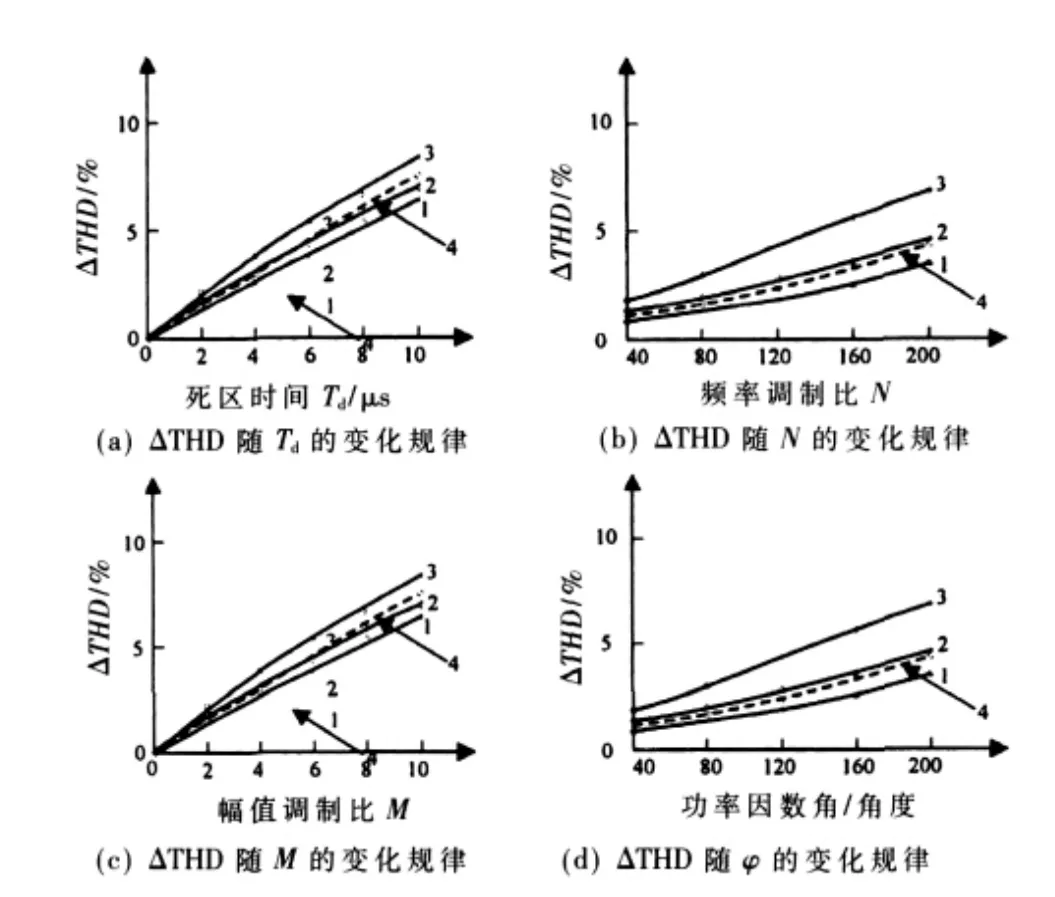
图5 ΔTHD变化规律曲线

在研究中均保持其他条件相同情况下，谐波总含量ΔTHD：(1)与 Td成正比，即死区越大，低次谐波含量越大，反之亦然；(2)与N值成反比，即N越大，谐波含量越小，反之亦然；(3)与M成反比，即调制比越大，谐波含量越小，反之亦然；(4)与φ成正比，即功率因数角越大，谐波含量越大，反之亦然。由图中可以看到,仿真曲线与理论曲线的变化趋势是一致的，在一定的误差范围内，理论计算值与仿真值存在少许差别是正常的。

由上述分析可知，死区效应对逆变器性能产生了许多有害的影响，且死区时间、逆变器的开关频率、调制比以及负载的功率因数等都会对其产生不同的影响。

(1)死区效应影响逆变器的输出基波电压。输出基波电压随死区时间的增加而线性减小；功率因数越大，基波幅值越小；开关频率越高，基波幅值下降越快。

(2)死区效应使逆变器输出电压波形增加附加谐波(主要是带来低次谐波),使输出电压产生较大的畸变。ΔTHD随死区时间的增大线性增大；功率因数越大，畸变率越小；开关频率越高，畸变率越大；调制比越小，畸变率越大。

因此在逆变器的设计上要综合考虑各方面的影响。另外，死区效应带来的主要是低次谐波，而低次谐波的抑制也较为困难，若采用滤波器会带来体积大、造价高及内部电压降等一系列不良后果。因此，对死区进行补偿是十分必要的。

参考文献

[1]刘陵顺，尚安利，顾文锦.SPWM逆变器死区效应的研究[J].电机与控制学报，2001(12)：237-241.

[2]程曙.SPWM逆变器死区效应分析[J].电力系统及其自动化学报，2002(4)：39-42.

[3]URASAKI N，SENJYU T，UEZATO K.An adaptive deadtime compensation strategy for voltage source inverter fed motor drives[J].IEEE Transactions.on Power Electronics，2005，20(5)：1150-1160.

[4]ITKONEN T，LUUKKO J，SANKALA A，et al.Modeling and analysis of the dead-time effects in parallel PWM twolevel three-phase voltage-source inverter[J].IEEE Trans.on Power Electronics，2009，24(11)：2446-2455.

[5]CHEN L，PENG F Z.Dead-time elimination for voltage source inverters[J].IEEE Transactions.on Power Electronics,2008，23(2)：574-580.

[6]佟为明.SPWM电压源逆变器变压变频过程的谐波分析[J].电力电子技术，1995，29(3)：47-57.