钱塘江江道水下地形冲淤分析研究
2011-07-02顾世杰
顾世杰,严 智
(1.浙江省钱塘江管理局,浙江 杭州 310016;2.上海成生科技有限公司,上海 200135)
1 问题的提出
钱塘江江潮水势变化引起钱塘江江道水下地形冲淤变迁。钱塘江管理部门多年来一直通过水下地形断面测量的方法,动态测量水下江道地形数值;尽管测量数值可以直观反映每个测点水下地形高程、固定断面折线图、固定水位下固定断面之间的江道容积,但不能直观解析水下地形的时空变化;传统方法是通过委托相关部门进行水下等深线等深面的图形制作,以图示方式进行对比分析来研究江道水下地形变化与冲淤情况。
为了方便快捷地分析与处理钱塘江水下地形的变化,通过引入水下地形插值方法,并研究水下地形的时空冲淤分析模型,开发相应的地形变化分析系统,对钱塘江水下地形的变化进行分析与管理,为钱塘江海塘安全管理提供相应的决策支持。
本文以钱塘江水下地形分析系统的研究与开发实践,探讨水下江道地形冲淤分析方法与技术路线,并提出相应的应用系统建设方案。
2 技术路线研究
水下江道地形冲淤分析研究主要涉及基础地形数据(包括海塘岸段的基础信息等)、基础江道地形数据、不同时段的江道断面测量数据。对江道地形的冲淤分析是依据不同的管理与决策需要进行不同时期的数据选择进行具体分析(不同年度、不同季节、不同的涌潮阶段的影响对比),因此除了建立基础的空间数据库外,需要针对水下地形建立时空数据库。
2.1 水下地形时空数据库
近来,由于信息化技术的发展与钱塘江基础地理信息系统的建设,为本研究提供了良好的基础数据支持与支撑,为此通过对钱塘江基础空间地理信息数据与分时段的水下断面测量数据分析处理,构建钱塘江水下江道地形时空数据库;并将历年的钱塘江江道水下地形测量信息,按照时间顺序建立江道地形的空间索引库,对江道地形统一管理。
2.2 插值方法比较分析
由于测点断面的离散性特点,水下地形测量数据并不能直观地反映水下地形地貌,因此需要通过相应的数学方法对水下离散点进行插值,重新构建水下江道地形。由于空间数据的相关性,选用不同的插值方法产生的地形效果与吻合度不尽相同,为此对不同的插值方法进行了比较研究,并应用实测数据进行案例验证。
2.2.1 Kriging插值法
Kriging是建立在变异函数空间分析基础上,对有限区域内的区域化变量取值进行无偏最优估计的一种方法。对于区域化变量 Z(x),设其在一系列采样点 x1,x2,…,xn上的观测值为Z(x1),Z(x2),…,Z(xn)。区域中某个网格点xn的估计值Z(x0)可用一个线性组合来估计,即

式中:λi为加权系数。假设 Z(x)满足内蕴假设,则有如下普通Kriging方程组:
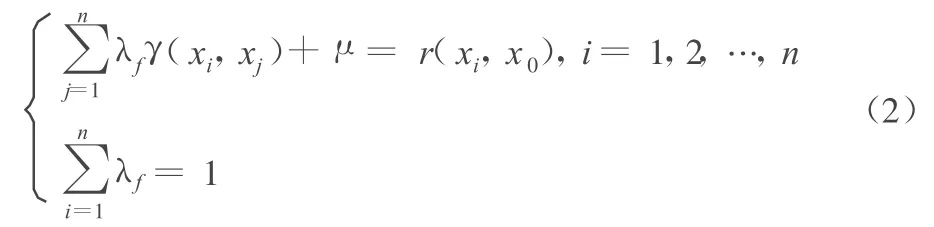
式中:γ(xi,xj)为采样点 xi与xj之间的变异函数值,μ为拉格朗日常数。由式(2)可得加权系数 λi,将其代入式(1)即可求得网格点x0的估计值Z(x0)[1].。
从求解Z(x0)的过程可见,Kriging插值的关键是如何获取变异函数γ(h)的最佳计算公式。这涉及2个主要问题,变异函数理论模型的选取和模型参数的估计。理论变异函数模型比较多,如何评定各种模型的有效性,需要进行深入的探讨。对于变异函数理论模型参数估计问题,由于理论模型常为非可微连续,而且参数较多,其实际上是一个多参数非线性优化问题。针对这个非线性优化问题,在变异函数拟合值与实验值的加权残差平方和最小的标准下,提出了一种遗传算法和模式搜索法相结合的方法来求解参数的最优解。
2.2.2 反距离加权插值法
反距离加权插值法(Inverse Distance to a Power)是1个加权平均插值法,可以进行确切的或者圆滑的方式插值。方次参数控制着权系数如何随着离开1个格网结点距离的增加而下降。对于一个较大的方次,较近的数据点被给定一个较高的权重份额,对于一个较小的方次,权重比较均匀地分配给各数据点。计算1个格网结点时给予1个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。距离加权法的特征之一是要在格网区域内产生围绕观测点位置的“牛眼”。用距离倒数格网化时可以指定1个圆滑参数。大于零的圆滑参数保证,对于一个特定的结点,没有哪个观测点被赋予全部的权值,即使观测点与该结点重合也是如此。圆滑参数通过修匀已被插值的格网来降低“牛眼”影响。
2.2.3 三角网插值法
三角网插值法是通过在数据点之间连线以建立起若干个三角形来进行,所有三角形的边都不能与另外的三角形相交,由此构成了由三角形拼接起来一张覆盖格网范围的三角网。每一个三角形定义了一个覆盖该三角形内格网结点的面,三角形的倾斜和标高由定义这个三角形的3个原始数据点确定,给定三角形内的全部结点都要受到该三角形的表面的限制。由于原始数据点被用来定义各个三角形,因此所有的测点数据都将参与插值建模。
2.2.4 Kriging插值法与反距离加权插值法、三角网插值法的比较
为了比较Kriging法与反距离加权插值法的优劣,这里采用了某次地形测量所获得的数据,分别进行Kriging插值和反距离加权插值,将插值结果绘制成等高线图,分别对应Kriging法与反距离加权插值法的插值结果,可以看到一些等高线会包住采样点,形成牛眼状的图形,与实际不相符合,这是因为Kriging法考虑到了采样点间的相关性。
2.3 水下地形冲淤分析计算
通过上述空间插值方法的分析比较,考虑钱塘江江道水下地形的特点,最终分别选用了空间三角网插值法与Kriging插值法对钱塘江江道断面测点数据进行处理,并构建水下三维地形模型,通过网格化插值与运算,生成覆盖整个江道的格点高程数据;通过空间定位匹配,建立以测点时间断面的分层时空数据库进行水下地形数据的管理与存储。
通常的冲淤分析是依据管理需求,选取特定的2个或多个时间断面的地形测值进行相互对比,以往的方法进行人工目测图形对比分析;为便于系统的统一处理,规定了钱塘江江道的标准化的基础网格,统一网络区间与格点位置;江道地形测点三维地形数据的存储采用统一的标准网格,进行冲淤分析时可以确保每一时段的水下地形在同一网格点进行对比分析,并运用后一时间断面地形数据与前一时段的地形数据,以同一空间格点进行比较计算,所求差值则反映所在格点的冲淤情况。差值为“+”值,则表明后一时间断面的高程值高于上一时段,则解析为此点淤积;反之,如果差值为“-”值,则表明当前时段的格点高程低于上一时段的格点高程,由此可解析为此点冲刷;所有格点差值可以构成所选时段的在此时间间隙中江道地形所发生的冲刷与淤积情况,并通过系统生成空间冲淤量的曲线和曲面。
关于冲淤泥沙方量计算则反映为冲淤曲面与0值平面的差的积分值,所有高于0值面的积分值表现江道淤积方量;而低于0值面的积分值则表现为冲刷方量。
3 应用情况
3.1 测点数据处理
将江道测量每个测点的数据包括平面坐标及高程信息导入数据库进行统一管理。
3.2 水下地形建模
3.2.1 DEM建模
根据水下勘测获取的离散高程点 (x,y,z)信息,采用基于三角形进行地形表面建模,将测深点连接成相互连续的三角面来模拟水下地形表面,并通过分区索引和空间索引,提高联网搜索速度。图1所示为江道地形实测高程点,图2为构建水下地形TIN化三角网图。

图1 水下地形测点数据图

图2 构建水下地形TIN化三角网图
3.2.2 等深线分析
采用空间三角网插值法和Kriging插值法对离散高程点实现插值,构成等深线(见图3)和等深面(见图4);同时按照时序进行比对,建立江道演变规律模型,支持直观图示与交互分析。
图3 水下地形等深线图

图4 水下三维等深面图
3.3 冲淤分析模型
利用同一地点不同时间的数据建立相同参数条件的DEM模型,将2个DEM模型叠加相减,结果如图5,在差值模型基础上进行冲淤量计算,得出结果值即为比较的结果。
采用格网模型,通过设定相同的格网参数,对应2期DEM模型数据,根据有效网点差值数据构成差值模型。

图5 水下冲淤分析结果图
4 水下地形冲淤分析系统建设
为完整地反映江道水下地形的全部地形地貌,重点在于对水下三维数字地形及江道冲蚀与淤积进行科学的分析。以下主要讨论数字水下地形信息系统建设内容:
4.1 江道测量数据管理与冲於分析
(1)江道测量数据管理:对历年的江道数据进行统一管理,并提供对数据查询与维护。
(2)三维水下地形生成:利用江道测量数据构建三维空间模型。
(3)滩地三维冲淤分析:通过对比历年的滩地三维数据分析滩地的冲於情况,为钱塘道江道演变提供数据支持。
水下地形分析将通过数字高程模型 (DEM,主要是描述地表面的高低起伏特性),设计以下功能模块,系统结构见图6。

图6 系统结构图
模块功能具体描述如下:
查询任意点的深度值,深度变化值 :
通过选定的任意一点,根据三角网中的选定点的坐标得到其水下高程值。
断面分析:提供测量断面、任意断面2种分析方法,测量断面的分析根据断面线和投影距离确定数据圈选范围,范围内的水深点在断面线上进行投影,依次连接所有的投影点得到断面分析结果。
任意断面的分析基于TIN模型,根据断面线端点在三角网中的位置得到端点的水深值,并计算断面线与模型中三角形边线的交点,根据交点位置计算交点的水深值,依次连接端点和所有的交点得到断面分析结果。
4.2 方量或容积分析
采用三角网插值法计算,通过建立TIN模型,将整个计算区域内的水下地形形成三棱柱集合。根据设定的水位值确定计算平面,再以选定的区域确定计算区域,将水位平面与江道地形曲面的差值,计算出容积结果。
4.3 冲淤分析
需要进一步在其基础上采用三角网插值法,选取不同测次以时间前后为顺序,进行江道地形曲面的插值,并得到新曲面,以不同的色彩带表示冲淤;在新的曲面下可进行冲淤值查询,“+”值为淤积,“-”为冲刷,同时可以选定任意区域进行冲量的分析计算。
5 结 论
钱塘江水下江道地形的冲淤分析与冲淤方量计算方法,经选取近年来的测量实测数据的处理与运算验证,对水下地形测量值采取插值方法,进行网格化处理,可以实现对江道水下地形处理并建立水下三维地形模型,运用空间格高程求差方法与空间三维积分计算能够实现水下地形的计算与分析,并方便用于系统运算。通过应用GIS技术与模型计算,可为钱塘江海塘安全管理提供更为科学、直观、方便、实用型的管理分析工具。
[1].曾怀恩,黄声享.基于Kriging方法的空间数据插值研究[J]..测绘工程,2007(5):5-8.
[2].白世彪,王军见,闾国年.Surfer软件在水下地形三维可视化与分析中的应用 [J]..海洋测绘,2004(5):51-53.
[3].王仁坤,闫红菱.建立三维地形模型的方法研究——利用梯度的离散点插值 [J]..水利水电科技进展,1996,16(6):25-27.
