互相关与阻尼比扰动混沌系统结合的检测方法

代慧1 朱洪雷2

（1.广东技术师范学院天河学院 2.广州番禺职业技术学院）

互相关与阻尼比扰动混沌系统结合的检测方法

代慧1 朱洪雷2

（1.广东技术师范学院天河学院 2.广州番禺职业技术学院）

基于互相关检测方法和阻尼比扰动Duffing振子检测系统的检测原理，提出了互相关与阻尼比扰动Duffing振子检测系统相结合的一种新检测方法。文中利用新检测方法在白、色噪声背景下对方波信号进行检测，仿真结果表明新检测方法的信噪比明显优于单独采用互相关检测方法或阻尼比扰动的混沌检测方法的信噪比，分别为－43.4dB、－42.1 dB和－40.5dB。

互相关；混沌；Duffing振子

1 引言

混沌理论应用于信息处理是现阶段混沌学发展的主要趋势。人们利用混沌系统对小信号极强的敏感性及对噪声的强免疫能力，将混沌理论用于检测微弱信号，在微弱信号检测[1,2]领域开辟了广阔的前景。

本文基于诸学者研究的基础上提出了一种新的检测方法——互相关与阻尼比扰动Duffing振子检测系统相结合。该方法更适合对微弱方波信号的检测。

2 传统的互相关检测原理

互相关方法[3]是常用的传统时域方法，互相关接收的抗干扰性比自相关好。当发送信号的重复周期或频率已知，可在接收端发出一种重复周期与发送信号相同的本地信号，将本地信号与混有噪声的输入信号进行互相关,就是互相关方法。图1所示是实现互相关检测的原理框图。

图1 互相关检测原理框图

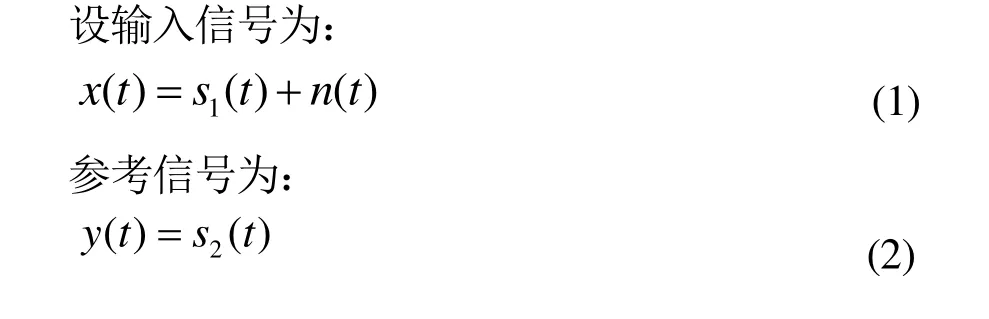
式中，s1( t)、s2( t)分别为周期信号，n( t)是噪声信号。则互相关函数：

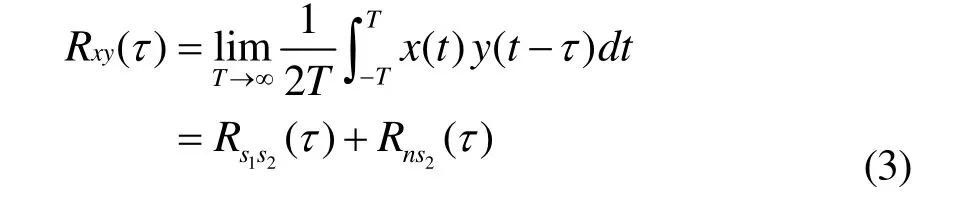
其中Rs1s2(τ)是s1( t)与s2( t)的互相关函数；Rns2(τ)是n( t)与s2( t)的互相关函数。如果s1( t)是已知的，可以设计参考信号s2( t)，使互相关函数Rs1s2(τ)随着自变量呈现明显的变化规律。由于参考信号s2( t)与输入噪声n( t)是互不相关的，只要假设n( t)或s2( t)之一的均值为零，则有Rns2(τ)=0，即：

目前传统时域方法处理信号的最低门限是－10dB[4]。

3 阻尼比扰动Duffing振子微弱信号检测原理

阻尼比扰动检测方法就是用被测信号扰动混沌振子系统的阻尼比参数。在系统的临界状态，阻尼比和策动力幅值有一定线性关系。理论分析，扰动阻尼比也能使Duffing振子系统的状态发生规律性变化，我们即通过这种变化来检测信号。

一般的扰动方式有相加或相乘，为通用起见，现采用相乘、相加相结合的扰动方式，如扰动为信号S，可得到如下的数学模型：

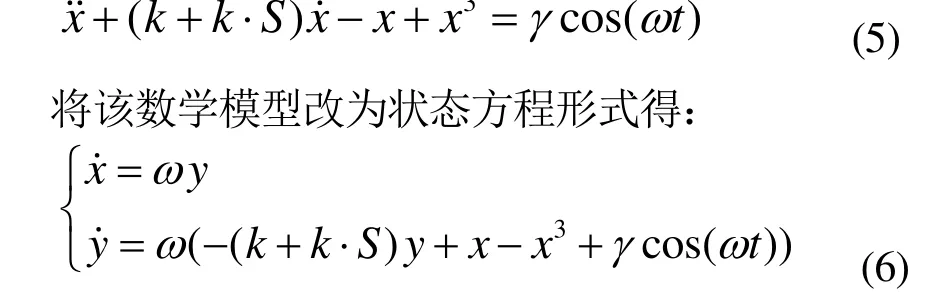
根据式(6)数学模型，在Matlab/Simulink软件环境下建立仿真模型一项本文不再重复,见文献[5]。

4 互相关与阻尼比扰动Duffing振子检测系统结合的检测方法

4.1 检测原理及检测模型

为了进一步抑制噪声，准确检测出待检周期信号，本节提出互相关检测方法与阻尼比扰动Duffing振子混沌系统相结合的检测方法。

互相关与阻尼比扰动Duffing振子混沌系统结合的检测方法结构图如图2所示，在Matlab/Simulink软件环境下建立仿真模型，如图3所示。

图2 互相关与阻尼比扰动Duffing振子混沌系统结合的检测方法结构图

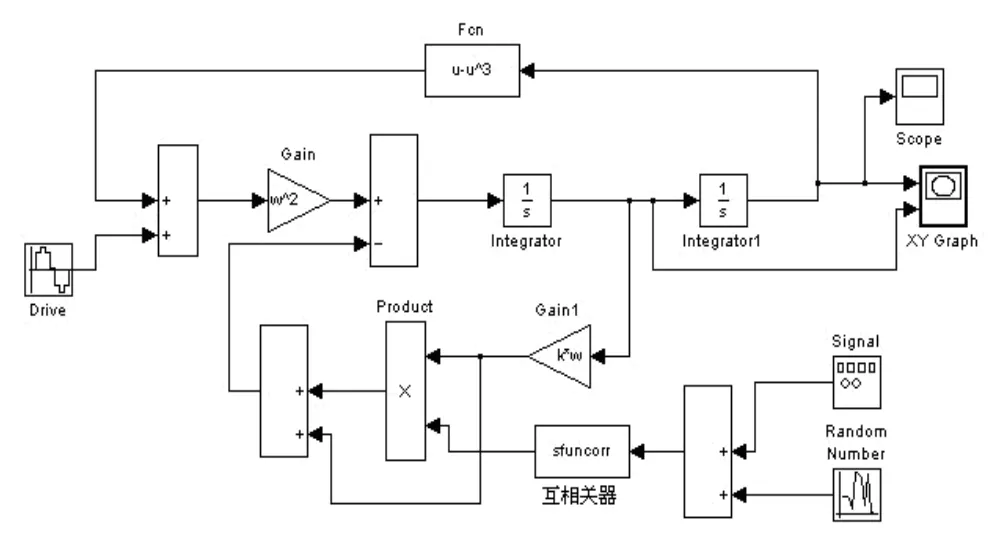
图3 互相关与阻尼比扰动混沌系统结合的仿真模型

本文所提出的互相关与阻尼比扰动Duffing振子混沌系统相结合的检测方法检测信号的思路是：首先将混有噪声的微弱方波信号输入互相关器，互相关器增强了周期信号，抑制了噪声信号，但输出的方波信号中仍含有一定的噪声。然后将从互相关器出来的信号并入到阻尼比扰动混沌系统中。最后根据相轨迹的变化或通过辨识系统(事先输入混沌判据)检测出信号。

4.2 白噪声背景下检测方波信号的仿真分析

设输入含有噪声的信号：

式中，a是待测周期信号的幅值，b是参考信号幅值，ω是待测信号的频率，n( t)是均值为零的高斯白噪声。

将系统的相轨迹设置为由混沌到大周期的临界状态，然后将高斯白噪声n( t)作为输入并入系统，由于输入信号中含有周期信号，所以系统相轨迹由大尺度周期状态跃变到混沌状态，见图4(a)、4(b)。

图4 加入白噪声前后系统的相轨迹

为更好的与文献[6]中的策动力扰动相比较，我们令n( t)=0.0459random(-1~+1)，经过大量仿真测得的信噪比门限如下：

4.3 色噪声背景下检测方波信号的仿真分析

高斯分布只是许多分布类型中的一种，非高斯信号更加普遍。本节将噪声分别变成高斯色噪声和非高斯色噪声，仿真实验步骤同白噪声背景下类似。

(1) 高斯色噪声

用方差为1的高斯白噪声通过一个四阶带通滤波器产生高斯白噪声n( t)。该滤波器的传递函数为：

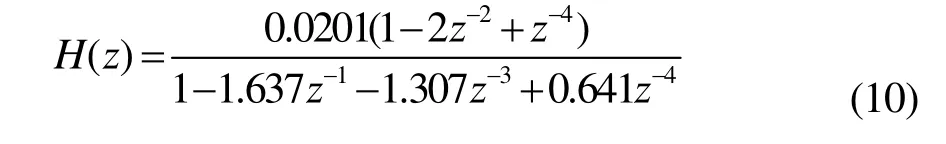
滤波器的上下限截止频率为0.2Hz，、0.15Hz。输入信号为仿真得到的信噪比门限为：

(2) 非高斯色噪声

用方差为1的非高斯噪声通过式(10)表示的四阶带通滤波器产生非高斯色噪声。仿真得到的信噪比门限为：

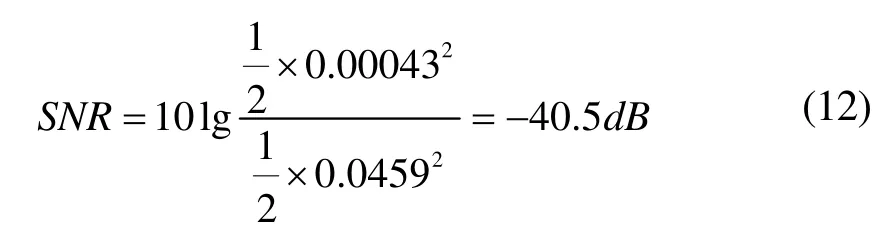
阻尼比扰动检测方法的信噪比是-23dB[4]。仿真结果表明，用互相关与阻尼比扰动的混沌系统相结合的检测方法来检测微弱信号，其输出信噪比门限有所降低，说明互相关环节对噪声有一定抑制。

5 结论

本文描述了互相关检测方法和阻尼比扰动的Duffing振子混沌系统的微弱信号检测方法，并在此基础上，提出一种独特的时域信号处理方案，将这两种检测方法结合起来构成新的检测系统——互相关与阻尼比扰动Duffing振子混沌系统相结合的检测系统。文中对新检测系统进行仿真建模，并应用新检测系统对微弱方波信号在白、色噪声背景下进行检测，仿真结果表明新检测方法的输入信噪比检测门限明显优于互相关检测方法以及单独采用阻尼比扰动的混沌检测方法，白色噪声背景下信噪比分别为－43.4dB、－42.1dB和－40.5dB。

[1] 戴逸松.微弱信号检测方法及仪器[M].北京:国防工业出版社, 1994.

[2] 曾庆勇.微弱信号检测[M].杭州:浙江大学出版社, 1996.

[3] 曾庆勇.微弱信号检测[M].杭州:江大学出版社, 1996.

[4] 聂春燕. 混沌理论及基于特定混沌系统的微弱信号检测方法研究[D].长春：吉林大学,2006.,

[5] 赵华.Duffing振子微弱方波信号检测方法的研究[D].保定:华北电力大学, 2006.

[6] 刘立.基于混沌理论的微弱信号检测方法研究[D].保定:华北电力大学, 2006.

The Detecting Method of the Mix Detecting Systems Combined Cross-Correlation Method with Disturbing the Damping Rate of Chaos Detection System

Dai Hui1Zhu Honglei2

(1.GuangDong Polytechnic Normal University Tianhe College 2. Guangzhou Panyu Polytechnic)

This article describes the detection principle of cross-correlation method and perturbation disturbing the damping rate of the duffing oscillator detection system, proposes a new detecting method combined cross-correlation with disturbing the damping rate of the duffing oscillator detection system. In the paper, square wave signal is detected under white /color noise background using the new method, its threshold of input SNR is significantly superior to cross-correlation method as well as disturbing the damping rate of the duffing oscillator detection method alone, and SNR is -43.4dB、-42.1dB and -40.5dB under white/colored noise background.

Cross-Correlation; Chaos; Duffing Oscillator

代慧，女，1983年11月出生，汉族，内蒙古，硕士，主要研究方向：微弱信号检测。