基于虚拟多用户模型的长码直扩信号伪码估计✴
2011-07-01白娟张天骐赵德芳包锐
白娟,张天骐,赵德芳,包锐
(重庆邮电大学信号与信息处理重庆市重点实验室,重庆400065)
基于虚拟多用户模型的长码直扩信号伪码估计✴
白娟,张天骐,赵德芳,包锐
(重庆邮电大学信号与信息处理重庆市重点实验室,重庆400065)
针对长码直接序列扩频(DSSS)信号的伪随机码(PN)盲估计问题,提出了一种新的周期长码直接序列扩频信号(PLCDSSS)模型。该模型等同于虚拟多用户短码扩频DS-CDMA系统,采用DS -CDMA的谱范数来估计同步偏移,该算法不需要更多假定限制,利用相关函数二阶矩、特征值分解和模糊酉矩阵方法就可以完成伪码序列的估计。实验结果表明,在较低信噪比下就可以完成对PN码序列的精确估计,表现出良好的性能。
直接序列扩频;周期长码;PN码;虚拟多用户;失步点盲估计
1 引 言
直接序列扩频(DSSS)通信[1]在发送端用PN码将原始信号的频谱扩展,这样信号能量几乎均匀地分散在很宽的频带内,从而大大降低信号的谱密度;在接收端,再用PN码解扩,使有用信号能量重新集中起来而输出最大。所以,直接序列扩频信号较之常规的窄带通信信号具有隐蔽性好、抗干扰、抗多址、反侦察能力强、截获概率低等优点而日益在民用通信和军事通信领域得到广泛的应用。但在非协作环境下,我们不知道观测信号所使用的扩频序列,而且信号可能完全淹没在噪声中,因此对直扩信号的检测、同步、均衡和估计变得越来越困难。虽然一些文献已经研究了直扩信号的盲检测、参数估计、同步和PN码序列估计等问题[2-5],但这些文献中的方法都是基于短码的情况,即用一周期PN码序列调制一位信息码,而长伪码直扩信号的伪码周期大于信息码周期,即一周期伪码调制多位信息码。这样,长伪码直扩信号具有更好的保密性和抑制多址干扰等优点而成为研究的热点。特别当长伪码直扩信号与PN码不同步时,长伪码序列估计变得更加复杂和困难。由于长伪码改变了伪码的周期和相关特性,从而基于短码的直扩信号参数估计方法就不能直接应用在周期长伪码扩频信号中。
针对长伪码直扩信号参数估计和长PN码序列盲估计的研究很少,目前已有的文献中,大部分都只对长码伪码周期进行估计[6],文献[7]研究了长伪码序列估计问题,但基于相关函数二阶矩的长伪码直扩信号模型形式较复杂。本文提出了一种新的虚拟多用户模型,该模型具有形式简单、易理解等优点,而且该模型等同于DS-CDMA系统,可以用DS-CDMA盲估计方法来估计PLC DSSS信号。同时,应用该模型不需要对信号作更多假设,采用一种模糊酉矩阵方法就可以完成对周期长伪码序列的盲估计。
2 信 号模型
周期长码直扩基带信号模型如图1所示。
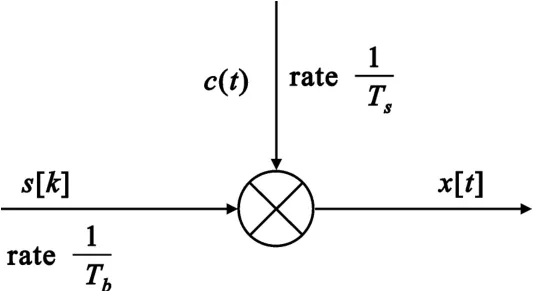
图1 周期长码直扩信号模型Fig.1 Model of PLCDSSS
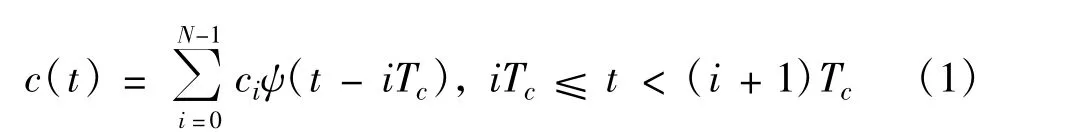
等同的虚拟多用户系统模型如图2所示。
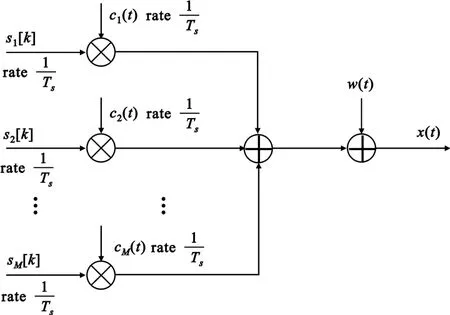
图2周期长码直扩信号的虚拟多用户模型Fig.2 Virtualmultiusermode for PLCDSSS
周期长伪码直扩信号的虚拟多用户系统数学模型可以表示为
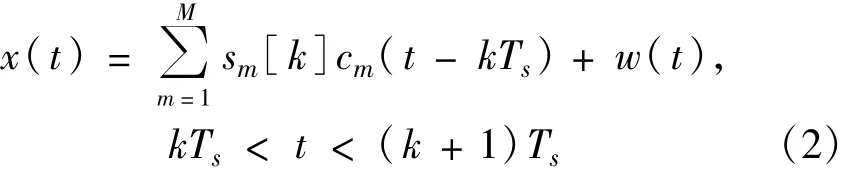
其中,cmm(t)和s[k]分别定义如下:
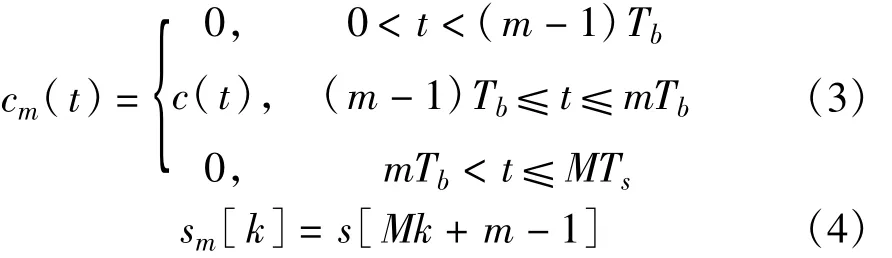
式中,m=1,2,…,M;w(t)为方差为σ2w的零均值高斯白噪声,并假设信息码、长伪随机码和噪声之间互相独立。
为了充分利用扩频码的扩频增益,我们用大于PN码码率的速率对接收信号进行采样,采样间隔为Δ=Ts/p,p为采样点数目,且p大于N,以Δ对接收信号进行采样后的离散形式为
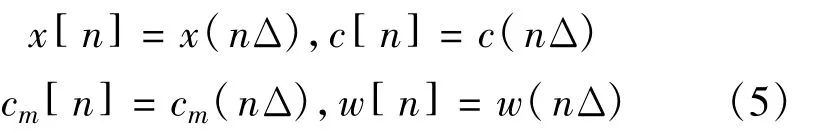
将接收信号分成时间上不重叠的数据窗,每个数据窗持续时间为周期长伪码PN码周期Ts。
由此得到式(2)的离散简化形式为
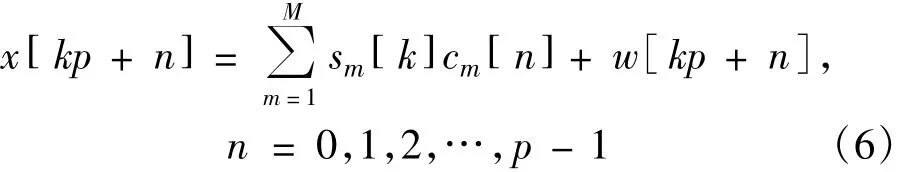
将接收的离散信号写成矩阵向量形式
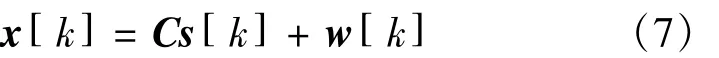
其中:
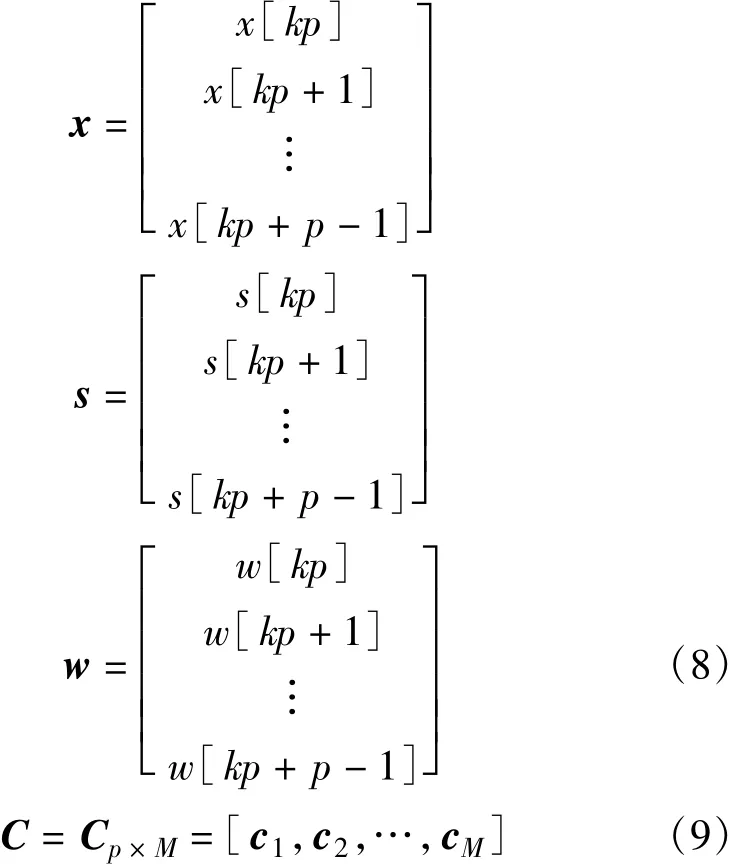
式中,cm(m=1,2,…,M)为第m个虚拟用户的扩频PN码。
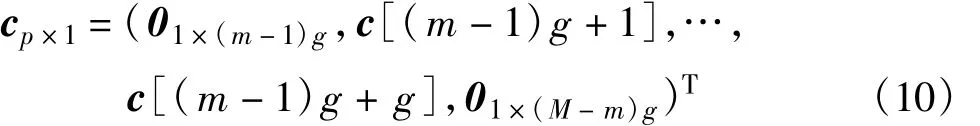
式中,g=p/M,g为每个虚拟用户的扩频码长度,这里规定g为整数。从式(10)可以看出,C为满秩矩阵,其秩为M,利用这一特性来估计周期长码PN码序列。
x表示一个时间窗内的采样数据向量,其自相关矩阵为Rx,维数为p×p。
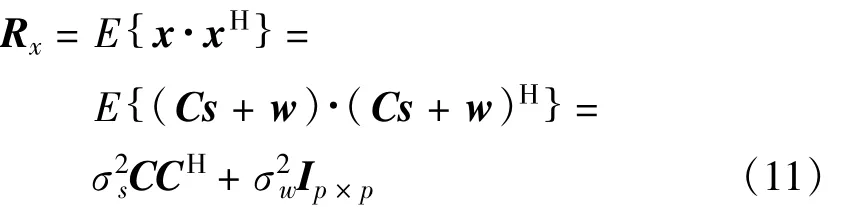
式中,σ2s为信号功率,则输入信噪比定义为SNR=
3 周 期长伪码直扩信号PN码序列盲估计算法研究
3.1 同步虚拟多用户周期长伪码直扩信号PN码盲估计
为简化分析,假设虚拟多用户已经完成了定时同步,则对自相关矩阵进行奇异值分解得到
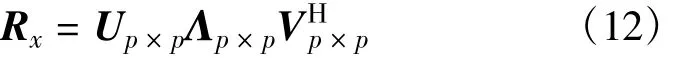
式中,U、V均为p×p维酉矩阵,U为特征向量矩阵,Λ为特征值对角矩阵。
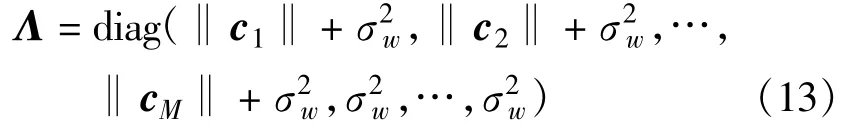
其中:
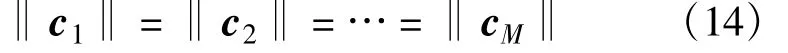
由式(13)和式(14)可知,一个时间窗数据阵包含M位完整的信息码,即Rx具有M个相同的特征值,并且这M个特征值对应的特征向量包含了PN码序列的各个部分,但由于M个特征值相同,因而无法按顺序依次取出特征向量,即无法从每个特征向量中提取出对应的PN码序列的各个部分。
由前面分析可知,C为满秩矩阵,其秩为M,则可以将U分成信号子空间和噪声子空间:
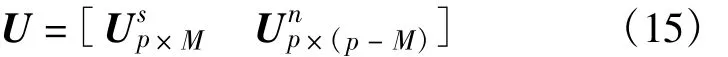
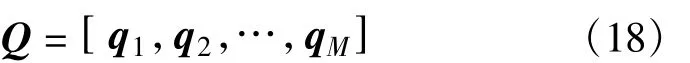

采用数学处理算法[8-9],由式(16)可以得到

Q定义如下:为M×1维列向量。将信号子空间Us分成如下形式:
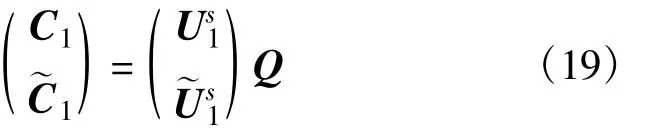
式中,Us1、C1分别为Us、C的前M() -1 g行矩阵,显然rank(C1)=M-1,由式(19)可以得到:由于QM×M为满秩矩阵,所以rank Us()1=M-1,比较式(20)两边最后一列列向量,可以得到:


由此可以得到qM:
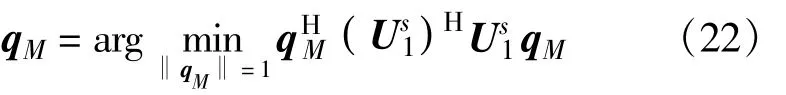
由于(Us1)HUs1只有一个零特征值,由式(22)可知,qM对应(Us1)HUs1最小特征值对应的特征向量。
当估计qM-j+1(j=2,3,…,M),我们依然将Us分成如下形式:
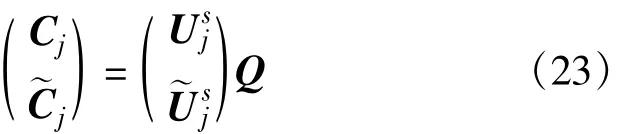
式中,Usj、Cj分别为Us、C的前(M-j)g行矩阵,此时rank(Cj)=M-j。同理,比较式(23)两边最后j列列向量,得到(Usj)HUsj有j个相同的零特征值,此时就不能直接从特征值分解中提取qM-j+1。

由矩阵分析[10]可知:
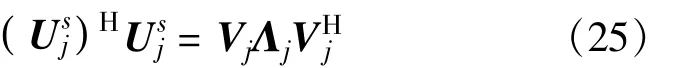
式中,Vj为特征向量矩阵,Λj为特征值对角矩阵。
将Vj进一步分成

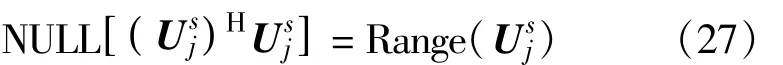
由式(27),我们可以通过如下形式得到qM-j+1:

式中,z为j×1维列向量,并且‖z‖=1。
同时定义
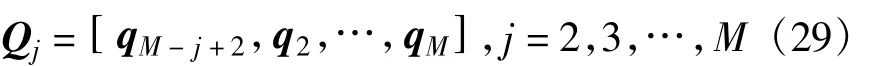
由于Qj为酉矩阵,可以得到

将式(28)代入式(30),可以得到

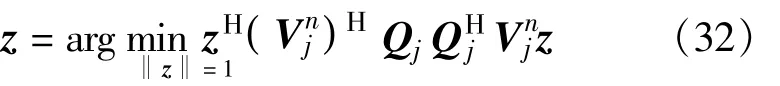

q1可以通过下式得到:
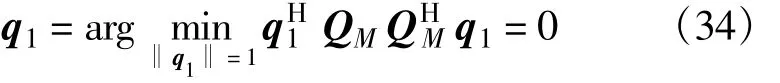
由此可知,q1为QMQHM最小特征值对应的特征向量。
到此,我们得到了整个QM×M,由式(17)我们可以得到C,即各个虚拟用户对应的周期长伪码的部分PN码序列。对各部分进行组合就可以得到整个周期长码的PN码序列。
3.2 基于谱范数的同步虚拟多用户失步点估计
上述周期长码直扩信号PN码盲估计算法中,我们假定已经完成了定时同步,而实际应用中,将接收信号分成时间上不重叠的数据窗进行处理时,并不知道发送端码元的起始位置,只有先估计出接收信号的失步点,才能完成周期长码直扩信号PN码序列估计。我们将每个数据窗的码元跳变点的位置定义为失步点。本文将周期长码直扩信号转化成虚拟多用户模型,可以将该模型看成同步DS-CDMA。
文献[7]中采用信号自相关矩阵的Frobenius范数估计失步点,由于周期长码直扩信号的一个PN码周期内包含M位信息码,所以要考虑失步点的偏移范围,不同的偏移范围需要计算相应的自相关矩阵的Frobenius范数,为了减小计算量,本文采用同步DS -CDMA中的谱范数算法[5]来估计失步点。
如前所述,将接收信号分成时间上不重叠的数据窗,若存在同步偏移,则将式(2)所示的接收信号改写成
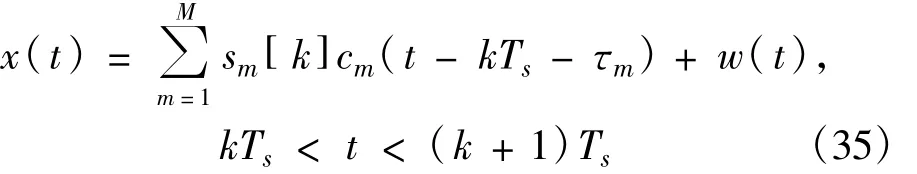
式中,τm为第m个虚拟用户的随机时延,也即失步点。本文中采用的虚拟多用户模型等同于同步DS -CDMA,即τ1=τ2=…=τM=τ,这样,一个伪码周期长度的数据窗将包含两位信息码,则其表达式为
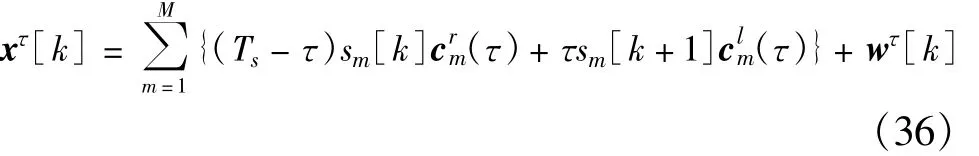
式中,crm(τ)、cml(τ)分别包含了一个完整周期扩频码的右边部分和左边部分,定义如下:
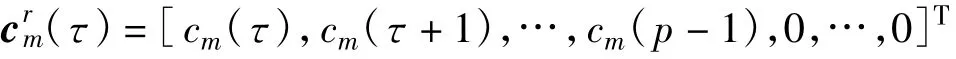
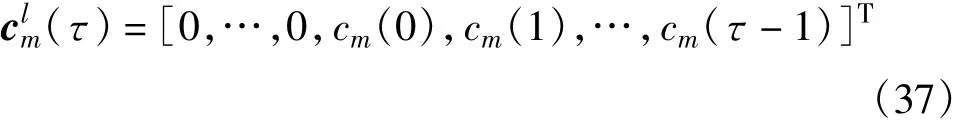
式中,wτ[k]为高斯白噪声向量。数据向量xτ[k]可以表示为一周期扩频码的右边部分crm与信息(Ts-τ)sm[k]的乘积与左边部分cml与信息τsm[k+1]的乘积的和。
将接收信号分成时间上不重叠的数据窗,可以得到

式中,每个数据窗持续时间为周期长码PN码周期Ts,τ为整个接收信号的失步点,N表示观察窗口数目。每个数据窗向量可以表示为所以可以选择以伪码周期为滑动窗口的长度对式(46)进行最大值搜索,达到最大时就得到失步点的估计值^τ:
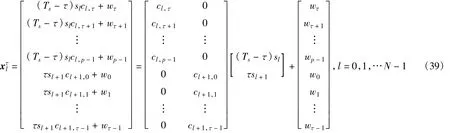

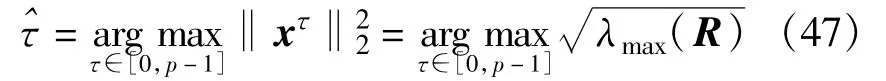
基于以上分析,周期长码直扩信号的盲估计算法步骤如下:
(1)将周期长码直扩信号模型建立为虚拟多用户直扩信号模型(式(2));
(2)用谱范数算法对接收信号的失步点τ∈[0,p)进行盲估计,得到^τ;
(3)运用本文提出的虚拟多用户PN码序列估计算法估计C;
(4)根据伪码序列的自相关特性,对C中的列向量进行组合相加进而正确估计整个周期长码PN码序列。
4 仿真
实验1:采用本文算法对周期长码直扩信号的PN码序列进行仿真实验:加入归一化零均值高斯白噪声,信噪比SNR=10 lg(σ2s/σ2w)=-8 dB;取扩频信号PN码长Nc=31位,采样率Sa=5 bit/chip,一个数据窗长度为p=Nc×Sa;数据窗数目选为N= 500;M=5,即一PN码周期含有5个符号周期,每个符号周期包含L=p/M个码片;τdelay=93。运用本文提出的谱范数算法完成失步点盲估计,则盲估计结果如图3所示。
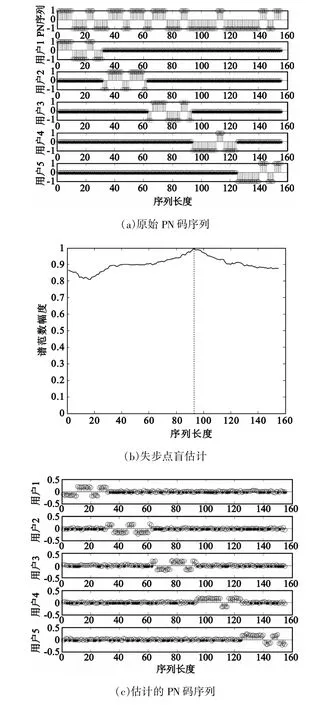
图3 高斯白噪声环境下虚拟多用户扩频序列盲估计Fig.3 Blind estimation of virtualmultiusers′PN sequence in AWGN channel
图3 (a)为虚拟5用户原始PN码序列,图3(b)和3(c)分别为同步虚拟5用户失步点和扩频码盲估计。由此可以看出,谱算法能较快较准确地估计失步点,而且不需要考虑文献[7]中同步偏移范围问题,从而减小了计算量。
实验2:验证本文提出的新算法的收敛性能,其结果如图4和图5所示。
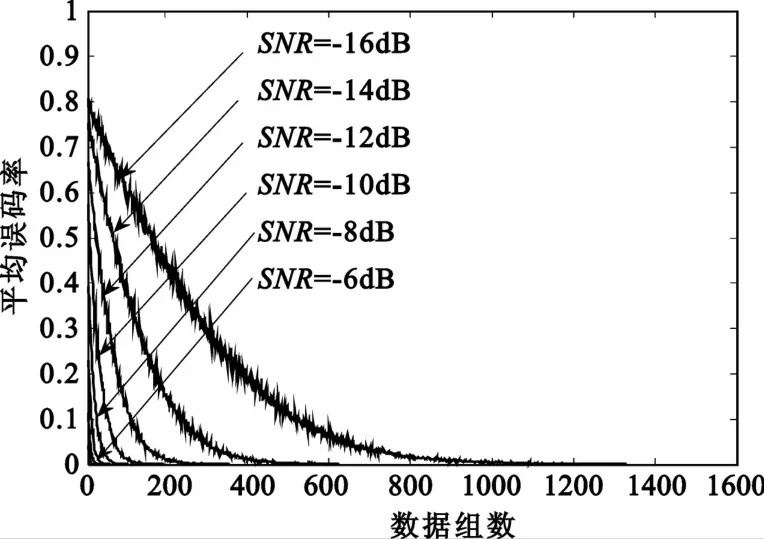
图4 不同信噪比下的收敛曲线Fig.4 The convergence curves in different SNR
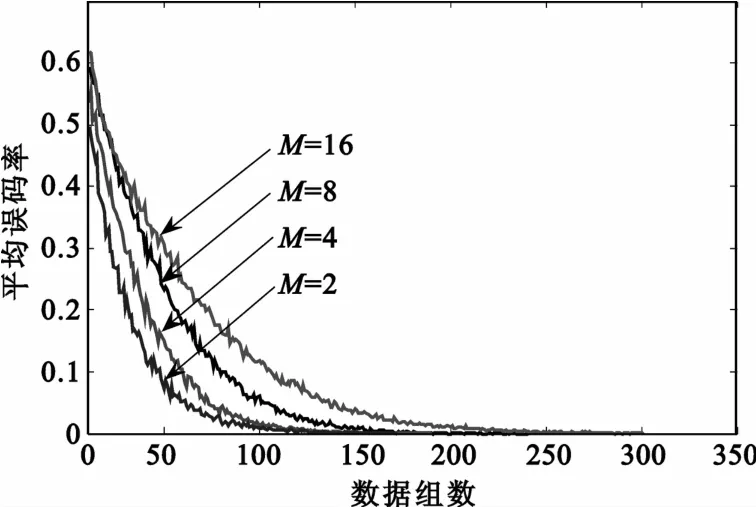
图5 不同调制位数M下的收敛曲线Fig.5 The convergence curves in different M
图4 为M=4时,一周期PN码序列调制4位信息码,在不同信噪比的情况下,估计的周期长码直扩信号的PN码序列的平均误码率随数据组数的增加的变化曲线,即不同信噪比下的收敛曲线。平均误码率是由M个虚拟用户平均误码位数之和再除以序列的位数得到的。每个虚拟用户的平均误码位数是对每一个信噪比的输入信号进行100次蒙特卡洛仿真然后求平均值得到的。从图中可以看出,随着数据组数N的逐渐增加,平均误码率逐渐减小,最终变为0;并且信噪比越高,平均误码率减小得越快,曲线收敛也越快,即所需数据组数越少。图5为SNR=-10 dB时,针对不同的M的收敛曲线。从图中可以看出,平均误码率随M增加而增大,且收敛速度变慢,即所需数据组数变大。由此可知,PN码序列的估计精度会随着信噪比的逐渐降低和M的逐渐增加而变差,但会随着数据组数的增加而不断提高,也即可以通过增加数据组数来进一步降低信噪比。
5 结论
本文提出了一种新的周期长伪码直扩信号的伪码序列估计算法,该算法将对长PN码序列的估计转化成对虚拟多用户伪码序列的估计。在此模型之上,首先扩展应用了盲多用户同步算法,然后运用相关函数二阶矩方法、特征值分解方法和模糊酉矩阵方法完成长PN码序列的盲估计。计算机仿真验证了该算法的有效性,该算法在较低信噪比(SNR= -16 dB)时,也能达到很高的估计精度,通过增加数据组数还可以进一步降低信噪比,而且增加M性能不会降低很多。同时,本算法采用虚拟多用户模型,这也为长伪码直扩信号参数盲估计问题提供了一种新的思路,可以将DS-CDMA参数盲估计方法应用到长码直扩信号参数估计中,但有待进一步研究。
[1]田日才,扩频通信[M].北京:清华大学出版社,2007. TIAN Ri-cai.Spread Spectrum Communications[M].Bejing:Tsinghua University Press,2007.(in Chinese)
[2]Burel G,Bouder C.Blind estimation of the pseudo-random sequence of a direct sequence spread spectrum signals[C]//Proceedings of the 21st Century Military Communications Conference.Los Angeles:IEEE,2000:967-970.
[3]程皓,郭伟.低截获直扩信号参数盲估计方法研究[D].成都:电子科技大学,2007. CHENG Hao,GUOWei.Study of Blind Estimation of DSSS signals[D].Chengdu:University of Electronic Science and Technology of China,2007.(in Chinese)
[4]张天骐,周正中.直扩信号伪码周期的谱检测[J].电波科学学报,2001,16(4):518-521. ZHANG Tian-qi,ZHOU Zheng-zhong.Detection of period for direct sequence spread spectrum signal[J].Radio Science,2001,16(4):518-521.(in Chinese)
[5]Youngho Jo,Dapeng Wu.Blind Synchronization Estimation of data symbol Spread sequence and generator polynomial in direct sequence spread spectrum systems[C]//Proceedings of 2008 IEEEMilitary Communications Conference.San Diego,CA:IEEE,2008:1-7.
[6]张天骐,周正中,邝育军.低信噪比长伪码直扩信号伪码周期的估计方法[J].系统工程与电子技术,2007,29(1):12-16. ZHANG Tian-qi,ZHOU Zheng-zhong,KUANG Yujun.Newmethod for periodic estimation of the PN sequence in the lower SNR long code DS-SS signals[J].Journal of Systems Engineering and Electronics,2007,29(1):12-16.(in Chinese)
[7]徐海涛,黄知涛,周一宇.长码直扩信号的伪码参数及序列的估计方法[J].西安电子科技大学学报,2007,34(增刊):51-54. XU Hai-tao,HUANG Zhi-tao,ZHOU Yi-yu.Algorithms for parameters and sequence estimation of the PN code in long code DS-SS signals[J].Jounal of Xidian University,2007,34(Suppl.):51-54.(in Chinese)
[8]Farid A A,Zhi-Quan Luo,ZhiDing.Blind Channel Equalization Based on Second Order Statistics[C]//Proceedings of 2005 IEEE International Conference on Acoustics,Speech and Signal Processing.Princeton:IEEE,2005:557-560.
[9]Daneshmand S,Aghaeinia H,Tohidian M,et al.Blind estimation of signal in periodic long-code DSSS communications[C]//Proceedings of2009 IEEE Sarnoff Symposium.Princeton,NJ:IEEE,2009:1-6.
[10]史荣昌,魏丰.矩阵分析[M].2版.北京:北京理工大学出版社,2005. SHIRong-chang,WEI Feng.Matrix Analysis[M].2nd ed.Beijing:Beijing Institute of Technology Press,2005.(in Chinese)
[11]TranterW H,Shanmugan K S,Rappaport TS,等.通信系统仿真原理与无线应用[M].肖明波,杨光松,许芳,等,译.北京:机械工业出版社,2007. TranterW H,Shanmugan K S,Rappaport TS,etal.Simulation Principle of Communication System and Wireless Application[M].Translated by XIAO Ming-bo,YANG Guang -song,XU Fang,et al.Beijing:Mechanical Industry Press,2007.(in Chinese)
BAIJuan was born in Shijiazhuang,Hebei Province,in 1985. She is now a graduate student.Her research concerns blind estimation of DSSS signals in complex environment.
Email:b-juan@163.com
张天骐(1971—),男,四川眉山人,教授,主要研究方向为宽带微弱无线电信号处理、盲信号与信息处理以及通信对抗理论与技术;
ZHANG Tian-qi was born in Meishan,Sichuan Province,in 1971.He is now a professor.His research interests includeweak wideband radio signal processing,blind signal and information processing,communication countermeasurement theory and technology.
Email:zhangtq@cqupt.edu.cn
赵德芳(1987—),女,河南辉县人,硕士研究生,主要研究方向为通信信号处理、计算机智能及应用;
ZHAODe-fang was born in Huixian,Henan Province,in 1987. She is now a graduate student.Her research concerns communication signal processing,computational intelligence and applications.
Email:defang1010@126.com
包锐(1983—),女(蒙古族),内蒙古通辽人,硕士研究生,主要研究方向为图像处理与数字水印。
BAO Rui was born in Tongliao,Inner Mongolia Autonomous Region,in 1983.She is now a graduate student.Her research concerns image processing and digitalwatermarking.
Email:mybr000@163.com
PN Sequence Estimation of Long-code DSSS Signals Based on Virtual M ultiuser M odel
BAIJuan,ZHANG Tian-qi,ZHAO De-fang,BAO Rui
(Chongqing Key Laboratory of Signal and Information Processing,Chongqing University of Posts and Telecommunications,Chongqing 400065,China)
For the blind estimation of long-code direct sequence spread spectrum(DSSS)signals,a new periodic long code(PLC)DSSSsignalsmodel as equivalent to a virtualmultiuser short-code DSSSsystem is presented.The spectral norm in the DS-CDMA system is exploited to estimate the synchronous offset,then secondorder correlation function,eigenvalue decomposition and ambiguitymatrixmethods are employed to estimate long -code spreading codes,without further restricting assumptions.Experimental results show that the algorithm can complete precisely the estimation of PN code in low SNR.The proposed algorithm has good performance. Key words:DSSS;periodic long code;PN code;virtualmultiuser;blind estimation of desynchronizing point
The National Natural Science Foundation of China(No.61071196);The NSAF Foundation of National Natural Science Foundation of China(No.10776040);The Program for New Century Excellent Talents in University(NCET -10-0927);The Project of Key Laboratory of Signal and Information Processing of Chongqing(CSTC,2009CA2003);The Natural Science Foundation of Chongqing(CSTC,2009BB2287,2010BB2398,2010BB2411)
TN911
A
10.3969/j.issn.1001-893x.2011.08.007
白娟(1985—),女(回族),河北石家庄人,硕士研究生,主要研究方向为复杂环境下的直扩信号盲估计;
1001-893X(2011)08-0029-07
2011-03-21;
2011-05-24
国家自然科学基金资助项目(61071196);国家自然科学基金-中物院NSAF联合基金项目(10776040);教育部新世纪优秀人才支持计划项目(NCET-10-0927);信号与信息处理重庆市市级重点实验室建设项目(CSTC,2009CA2003);重庆市自然科学基金资助项目(CSTC,2009BB2287,2010BB2398,2010BB2411)
