基于时频分析的相位编码信号检测及识别方法研究

杨国彬,郑志娟

(上海微波设备研究所,上海 201802)

0 引 言

随着雷达技术的快速发展,常规脉冲雷达信号在雷达信号环境中的比例已减少,线性调频、非线性调频、相位编码等雷达信号逐渐增多。基于目前的复杂雷达信号环境,要求电子对抗要有更高的信号检测手段,并对检测到的信号进行分选和识别时提出了更高的要求,因此需要采用频域检测方法对低信噪比信号进行检测及对其脉内特征进行分析。

现在出现的这些复杂雷达信号不仅在时域有复杂的变化,在频域上的变化方式也很多,这就是所谓的时变信号或非平稳信号。那些基于傅氏分析的常规处理方法已经无法对这些信号进行分析,而必须采用时频分析方法。时频分析方法不仅说明了存在什么频率,而且指明了在什么时间存在,因此,时频分析方法是研究这种非平稳信号最有力的工具之一。本文首先采用时频分析(短时傅里叶变换)技术对信噪比为0 dB环境下的脉冲信号进行检测,然后对检测到的信号进行脉内调制类型识别及参数估计。目前,研究脉内分析方面的文章很多,而且在高信噪比条件下能够实现对这些时变雷达信号的分析与识别,但是,在低信噪比条件下就很难实现对这些信号的检测与识别,特别是对相位编码信号的分析处理更是脉内分析中的难点。为此,本文提出了一种基于时频分析(短时傅里叶变换)对相位编码(四相编码(BPSK)/六相编码(QPSK))信号进行检测及调制类型的识别方法,实现了在低信噪比(0 dB)条件下对BPSK/QPSK信号的检测及识别。并通过计算机仿真实验证明了该方法的有效性。

1 时频分析与脉冲检测

1.1 短时傅里叶变换

傅傅里叶变换公式为:

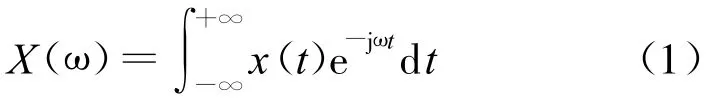
由式(1)可以看出,为了由傅氏变换研究1个模拟信号的谱特征,必须获得信号在时域中的全部信息,甚至包括将来的信息。这给实际应用带来了一定的困难,而且1个信号一经傅氏变换就等于失去了时间,给出的只是频谱信息,也就是说它不能作时频分析。为了克服这个不足,D.Gabor1946年在论文中为了提取傅氏变换的局部信息,引入了1个时间局部化的“窗函数”g(t-b),其中参数b用于平移动窗以便覆盖整个时域。这就是一般所谓的“短时傅里叶变换”(STFT),其表达式为:

由式(2)可以看出,在t时刻的STF T就是信号x(τ)与1个移动的以t为中心的“分析窗”g(τ-t)相乘以后的傅里叶变换,由于与1个相对短的函数g(τ-t)相乘就有效地抑制掉了分析时刻τ=t通道以外的信号,则STFT(t,ω)就是信号 x(τ)在分析时刻τ=t附近的简单的局部谱。这种变换是集时间表示与频率表示于一身的分解,这也是前面介绍的时频分析方法之一。本文就是利用这种时频分析方法对雷达信号进行检测并对脉内调制类型进行识别的。

1.2 脉冲检测

雷达信号通常为一系列脉冲串,如果信号采样是盲采,那么采样数据中既包含脉冲信号部分,也包含脉冲间隔部分,因此在进行脉内分析之前必须首先确定脉冲所在位置,即检测到脉冲的到达时间(TOA)和脉冲宽度(PW)。通常脉冲检测的方法有时域幅度检测、频域检测及瞬时自相关积累检测等。这3种检测各有优缺点:时域幅度检测法检测的速度快、但是对信噪比要求较高,只能在高信噪比条件下进行检测;瞬时自相关积累检测对信噪比要求较低,但是不能处理多信号的情况;频域检测能处理低信噪比及多信号的情况,但是,该方法很难计算信号的脉宽。因此,本文采用短时傅里叶变换的时频分析检测方法对低信噪比信号的脉冲进行检测。时频分析技术旨在构造一种时间与频率的联合密度函数,以揭示信号中所包含的频率分量及其演化特性,即时频分析方法不仅说明了存在什么频率,而且指明了在什么时间存在。因此,该检测方法不仅能处理低信噪比及多信号的情况,而且还能够很容易地计算信号的脉宽。该检测算法的主要步骤为:

(1)根据数据长度及所需检测脉冲到达时间的精度来确定滑窗长度、滑动步长及做FFT的长度;

(2)待所有滑窗数据都进行完FFT变换之后,把得到的频谱数据结合起来绘出时频分析曲线图;

(3)根据时频分析曲线图中的频率幅值确定动态检测门限;

(4)根据滑窗长度和滑动步长数据关系,由动态检测门限确定出检测的脉冲数量、脉冲到达时间及脉冲宽度;

(5)输出检测结果。

检测的流程框图如图1所示。

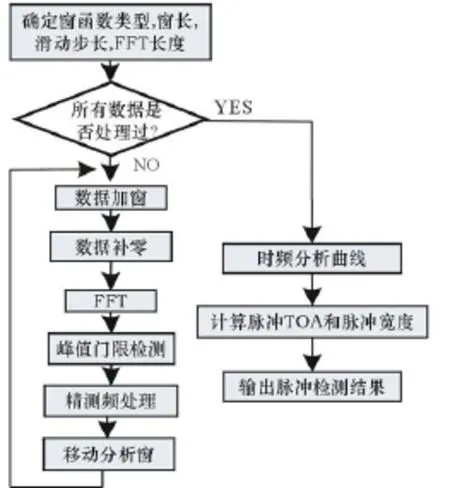
图1 基于STFT脉冲检测流程图

2 相位编码信号模型及特征分析

相位编码调制信号的时域表达式为:

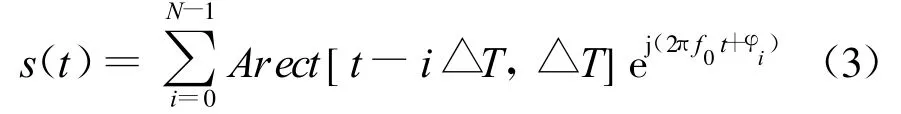
式中:N为子码数;△T为子码宽。

当φi取0或者π时,式(3)表示为 BPSK调制信号;当 φi取 π/2、π或 3π/2 时,式(3)表示为QPSK调制信号。也就是说,二相编码(BPSK)信号的相位跳变为π/2,而四相编码(QPSK)信号的相位跳变为π/2、π或3π/2。现在来分析一下,信号相位跳变π/2、π或 3π/2时,信号的频谱特征。

设待分析信号为:

该信号的频率为 ω0,分下列3种情况讨论,据式(1)对该信号作傅氏变换:

其中T=T1,现举一信号为例来说明上面所得到的傅氏变换结果:

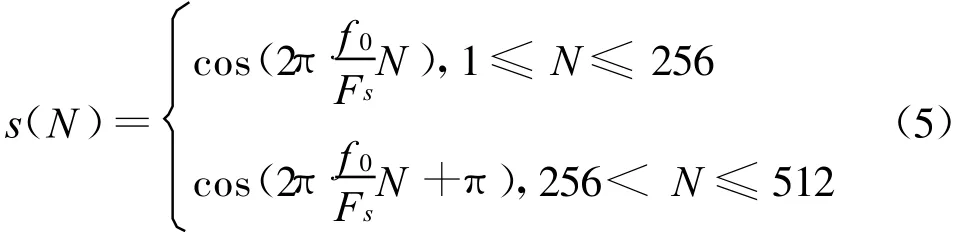
式中:f0=50 Hz,Fs=1 MHz。

该信号的数据长度为512点,在256点处相位跳变了π,条件符合上面提到的第2种情况,对该信号作傅氏变换,其结果如图2所示。

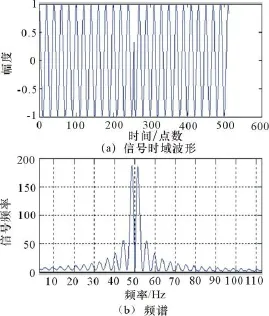
图2 式(5)信号的时域和频域图

对于单频信号,其幅频特性曲线应该是在该信号频率处幅度值最大,但是,从上面3种情况的推导结果可以看出,相位跳变π的信号其频率处的幅度值为零,相位跳变π/2或3π/2的信号其频率处的幅度值为,相位不跳变的信号其频率处的幅度值为,由此根据3种情况下信号频率处的幅度值不同,建立起了三者之间相互区别的特征。

这样就可以利用短时傅里叶变换对信号进行时频分析,这里所用的窗函数为一矩形窗,宽度等于观测时间。通过得到的时频分布曲线便可以确定信号相位是否有跳变以及跳变的时刻和跳变的大小,从而便可以实现对BPSK/QPSK调制信号的分析与识别。

3 信号实例仿真分析

为了验证上述方法的有效性,本文采用Matlab对直接由任意波形发生器产生的 BPSK和QPSK信号调制并经过模/数(A/D)转换采集存储的脉冲信号进行了分析测试。下面以码元长度为13的二相编码(Barker码)信号和码元长度为7的四相编码信号为例进行分析。

信号a参数:采样频率为2 GHz/s;采集数据长度为2 M;信号频率为 400 MHz;脉宽为 20 μ s;调制类型为二相编码;编码规律为1111100110101;码元宽度为1.5 384 μ s;码元长度为13。

信号b参数:采样频率为2 GHz/s;采集数据长度为1 M;信号频率为100 MHz;脉宽为 7 μ s;调制类型为四相编码;相位变化规律为 π/2,π,0,3π/2,π;码元宽度为 1 μ s;码元长度为7。

信号的时域波形及基于短时傅里叶变换的时频分析曲线如图3所示。

利用基于短时傅里叶变换的时频分析检测法检测出脉冲后,计算出各脉冲的到达时间和脉宽后,再利用时频分析技术对单个脉冲进行分析,分析结果如图4、图5所示。图中:(a)是信号时域波形和时频分析,(b)是信号相位实际变化的曲线,图右侧下是分析得到的结果。根据前面的理论结果,在时域信号相位跳变处,在时频分析曲线的相应时刻也应该有突变。

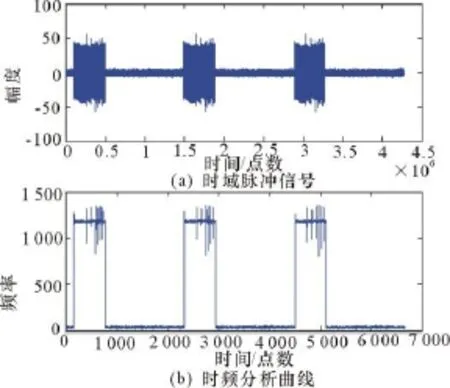
图3 时域波形及时频分析特性曲线

实际分析的情况也正是如此,如图所示,在时频分析曲线上有尖峰的地方就是相位跳变处,而且根据各尖峰的幅值来判断相位是跳变π还是跳变3π/2(由前面的理论结果可知,相位跳变π/2或3π/2时,其信号频率处的幅度值相同。

因此,本方法无法区别相位是跳变 π/2还是3π/2,从而可以判断该信号是否为相位编码信号,并进一步判断是BPSK还是QPSK调制信号。

图4 a信号分析结果

图5 b信号分析结果

下面给出算法的判别过程:

(1)Aigu(m1)＞Th1

(2)Th2＜Aigu(m2)＜Th1

其中Aigu()表示尖峰幅值;m1和m2表示尖峰数量;Th1和 Th2分别表示检测门限 1和检测门限2。

对BPSK调制信号进行解码时,用1、0之间的变化表示相位跳变π;对QPSK调制信号进行解码时,用10代表相位跳变π/2或 3π/2,用 11代表相位跳变π,紧随其后的数字代表跳变后的码元个数。在此噪声环境下,Monte Carlo模拟进行1 000次,识别准确率可达到100%。

然后,用 random()函数给信号 a、b加入随机噪声,使信噪比都达到0 dB,信号的时域波形及基于短时傅里叶变换的时频分析曲线如图6所示。

从图6可以看出,在信噪比为0 dB环境下,脉冲完全淹没在噪声中,根本无法利用时域法进行检测,利用短时傅里叶频域检测,虽然时频分析曲线变化比较恶劣,但是从时频分析曲线上还是能明显的看到有3个脉冲存在,经过进一步的软件算法处理,还是能比较精确地计算出各脉冲的到的时间和脉冲宽度。

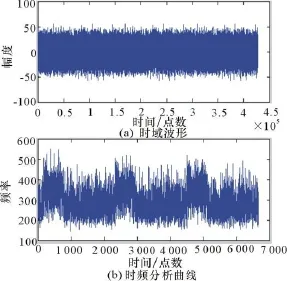
图6 时域波形及时频分析特性曲线

对检测出来的脉冲,再用时频分析技术进行脉内分析,Monte Carlo模拟同样进行1000次,分析结果如图7、图8所示,在此噪声环境下,识别准确率可达到98%以上。

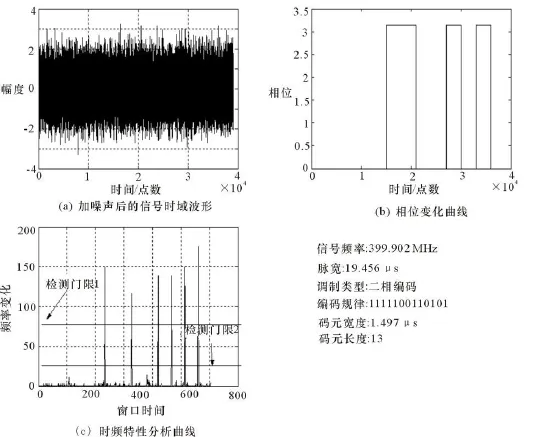
图7 a信号在0 dB下的分析结果

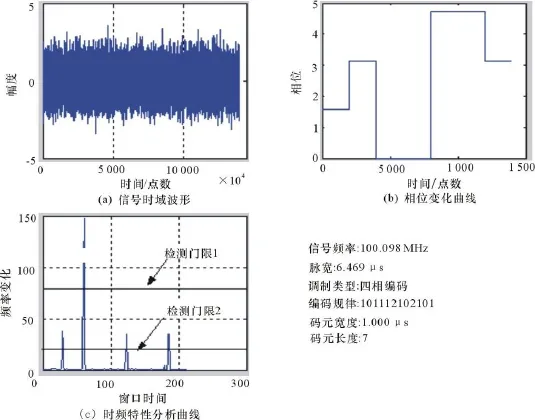
图8 b信号在0 dB下的分析结果

分析结果验证了本文经过理论分析而得到的检测及识别方法的有效性,从而实现了低信噪比条件下对BPSK/QPSK调制信号的检测及识别。

4 结论

本文首先给出了分析非平稳信号的主要方法——时频分析方法,然后根据理论推导结果,建立低信噪比环境下的信号检测算法,该算法既能处理低信噪比及多信号的情况,还能够很容易地计算出信号的脉宽,弥补了现有常规信号检测方法的缺陷;然后,针对相位编码信号(BPSK/QPSK)的具体特点,建立了专门的识别算法,该识别算法的主要优点是,能够实现低信噪比(0 dB)条件下对相位编码信号(BPSK/QPSK)的识别及参数估计,克服了现有方法在低信噪比条件下对相位编码信号处理的难题。计算机仿真分析结果证明了该信号检测及识别算法的有效性,说明在低信噪比的条件下,用本文提出的算法能进行BPSK/QPSK信号的检测和识别。

[1]刘庆云,李志舜.确定性时变信号的分析与处理方法研究[D].西安:西北工业大学,2004.

[2]张贤达.非平稳信号分析于处理[M].北京:国防工业出版社,1998.

[3]黄知涛,周一宇,姜文利.基于相对无模糊相位重构的自动脉内调制特性分析[J].通信学报,2003,24(4):30-33.

[4]毕大平,董晖,姜秋喜.基于瞬时频率的脉内调制识别技术.电子对抗技术,2003,20(2):6-10.

[5]那云諕,司锡才.二相编码信号调制分析与识别[J].系统工程与电子技术,2004,26(3):298-332.

[6]科恩.时-频分析:理论与应用[M].西安:西安交通大学出版,1998.

[7]Harry L,Van T rees.Detection,Estimation,and Modulation Theory[M].北京:电子工业出版,2003.