接触网可靠性研究方法浅析

陈 兴

0 引言

接触网作为电气化铁道的重要组成部分，结构复杂，具有大跨度、高柔性、几何非线性等特点，线长点多，极易受环境因素的影响。由于接触网沿铁路线路布置，绝大部分裸露于自然环境中且无备用，一旦出现故障将导致列车停驶，因此其安全问题已经成为电气化铁道改造的难点。随着电气化铁道运营范围的不断扩大和列车速度的提高，对接触网可靠性展开研究已迫在眉睫，提高接触网的稳定性和可靠性对于减少电气化铁道运行故障,改善运行效率具有举足轻重的作用。

1 国内外接触网可靠性研究现状

日本于20世纪70年代对新干线高速铁路及机车车辆开展了可靠性研究工作；1980—1982年，推测出电力机车和动车的可靠度。美国联合太平洋铁路公司建立了完善的可靠性系统，使机车及其零部件的可靠性评价由定性分析提高到定量分析的阶段。英国、德国等国家对可靠性工程进行了研究，形成了一系列标准，如 EN61025、EN60300、EN50126等。

与国外相比，国内铁路部门可靠性工程的研究起步较晚，应用较少。研究主要集中在“车辆可靠性”方面，接触网可靠性的研究较少，尚处于初级阶段。1993年国内首次提出接触网可靠性问题。文献[2]探讨建立了单边、双边2种供电方式下供电臂的供电可靠性指标计算公式；文献[3]介绍了接触网典型零部件的可靠性设计方法，总结了接触网系统可靠性工程的研究范畴；文献[4]将可靠性引入铁路电气化领域。另外，文献[5]提出了牵引供电系统实行可靠性系统工程的必要性，实现步骤和方法。

2 接触网主要故障分析

目前国内正在运营的接触网设备主要存在如下几个问题：

（1）接触线或承力索的内力超过许用值，引起导线拉断。

（2）支持结构或构件的内力超过许用值，引起构件折断。

（3）导线质量参差不齐，疲劳磨损严重，断线事件时有发生。

（4）由于施工工期、工艺等问题，施工质量不能完全符合标准要求，导致接触网自投入运营之日起即隐瞒了事故隐患。

（5）铁路运量增速较快，供电维修“天窗”兑现率低，供电设备长期处于失修状况，再加上零部件性能不稳定，往往不能及时发现、更换而导致发生故障。

（6）外部环境影响导致接触网事故，特别是风、霜、雨、雪、沙等环境对接触网结构可靠性的影响严重。

3 接触网部件强度可靠性分析模型

对接触网各部件来说，应力S和强度R相互作用决定了它们的可靠程度，它们都是服从某种概率分布的随机变量，其中

式中，XRi为与结构强度有关的量，如结构的尺寸、材料性质等；XSj为与应力有关的量，包括各种负载。这里的应力和强度都是广义上的概念，在磨损分析中，它可以分为磨损量和最大允许的磨损量。以X = (X1, X2,…Xn)表示基本随机参数向量，则功能函数可表示为

当g(X)＞0时，表示该部件处于正常工作状态，它的可靠度Pr就是g(X)＞0的概率。相反，失效概率Pf是g(X)＜0的概率，表示该部件丧失工作能力，此时，应力和强度发生了干涉现象。如果用fs(s)、fR(r)、fRS(r,s)分别表示应力S、强度R的概率密度和它们联合的概率密度，且当S、R独立时，Pf、Pr分别为

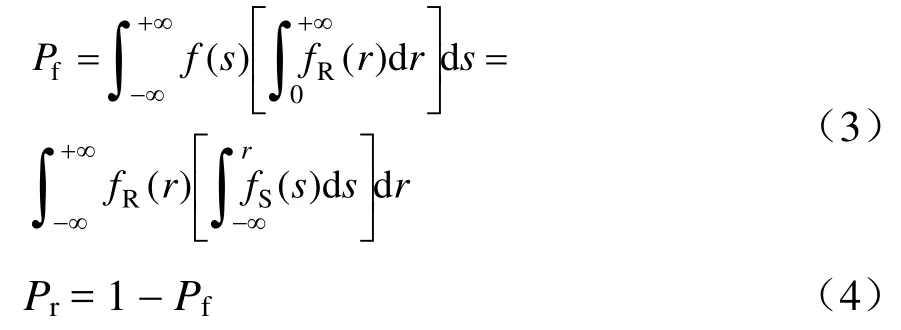
强度可靠性分析干涉模型如图1所示，得到可靠性指标为[6]

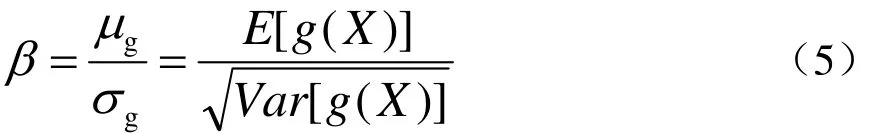
如果基本随机参量服从正态分布，则有

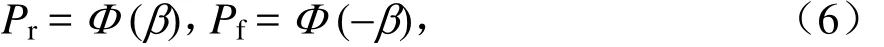
式中，Φ(·)为标准正态分布函数。

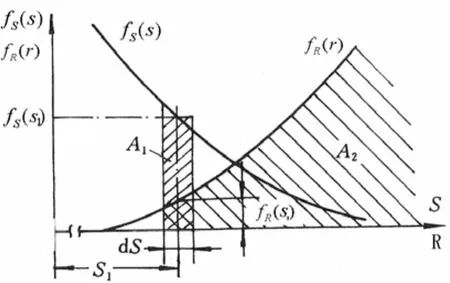
图1 接触网部件强度可靠性分析干涉模型曲线图

由应力-强度干涉图可看出，当零件的强度和工作应力离散程度越大时，干涉部分就可能增大，零件的不可靠度也就加大；材料的性能愈好，工作应力愈稳定，则它们的分布离散度将减小，零件的可靠度也就愈高。

4 接触网部件强度可靠性计算方法

由式（3）可见，可靠度可由数值积分来求解，但计算量太大，同时，对于许多复杂问题，状态函数g(X)的联合概率密度也很难确定，因此在实际中常采用近似方法。常用的数值方法有4种[7～10]。

（1）蒙特卡罗递进法。蒙特卡罗递进法的基本思想是首先在失效面上选取初始抽样域，然后根据每次抽样所获得的信息，通过逐步收缩抽样区间确定设计验算点，达到求解可靠度指标的目的。对于可靠度指标较大的情形，设计验算点往往不在设计变量均值附近，而设计变量的概率密度在均值附近往往较大，如果不能预先较准确地估计设计验算点的位置，则计算的结果会有很大的误差。

（2）一次二阶矩法。一次二阶矩法在实际工程中应用相当广泛，已成为国际上零件可靠度分析和计算的一种基本方法。其基本思想是根据基本随机变量的前二阶矩，将非线性功能函数在随机变量的均值点进行Taylor展开并保留至一次项，然后近似计算出功能函数的均值和标准差，进而求得可靠性指标或可靠度。该方法最大的优点是计算简便，但存在以下缺陷：a.不能考虑随机变量的分布形式，只适用于基本随机变量服从正态或对数正态分布的情况；b.将非线性功能函数在随机变量均值处展开，展开后的线性极限状态平面可能与真实极限状态曲面的偏离程度较大，会带来相当大的误差；c.选用不同的极限状态方程会得到不同的计算结果。

（3）验算点法（JC法）。作为一次二阶矩法的一种改进方法，JC法不在均值点处进行 Taylor展开，而是在通过极限状态方程g(X) = 0上的验算点处进行展开。针对非正态随机变量，JC法首先需要将非正态随机变量进行等效正态化，在设计验算点处使等效正态分布函数的累积概率分布函数（CDF）值和概率密度函数（PDF）值分别和原随机变量的CDF值、PDF值相等。通过迭代求解，计算出零件的可靠性指标和可靠度。JC法克服了一次二阶矩法的不足，适用于任意分布形式的随机变量，并且对于非线性程度不高的结构功能函数，其精度可以满足一般工程需要。由于该方法被国际结构安全联合委员会（JCSS）所推荐，故称JC法。

（4）径向基神经网络原理及算法。结合环境荷载对接触网体系的作用特征和荷载的参数变化，建立两相流CFD数值模拟的数学模型，提出了荷载与结构响应的组合原则，为定量研究荷载对接触网结构的影响提供了新的方法。该方法针对接触网的结构特点，基于特征响应点的风振响应时程，将动态增量法引入到 Budiansky-Roth稳定性判定准则，提出了适合接触网结构的动态稳定性判定准则，得出了接触网的主要结构参数对其动态稳定性的影响规律。基于最大负载概率分布函数、结构应力响应时程和 Palmgren-Miner线性疲劳累积损伤准则，提出了接触网结构疲劳可靠度计算方法。图2所示为有R个输入、h个神经元和 K个输出的RBF神经网络结构。输入层节点只传递输入信号到隐层，对输入数据不进行任何处理；隐层为 RBF神经元层，其作用函数（基函数）是RBF，完成从输入空间到隐含层空间的非线性变换；而输出层采用Purelin函数，它将隐层各节点的输出进行线性组合，产生最终对输入的响应值。

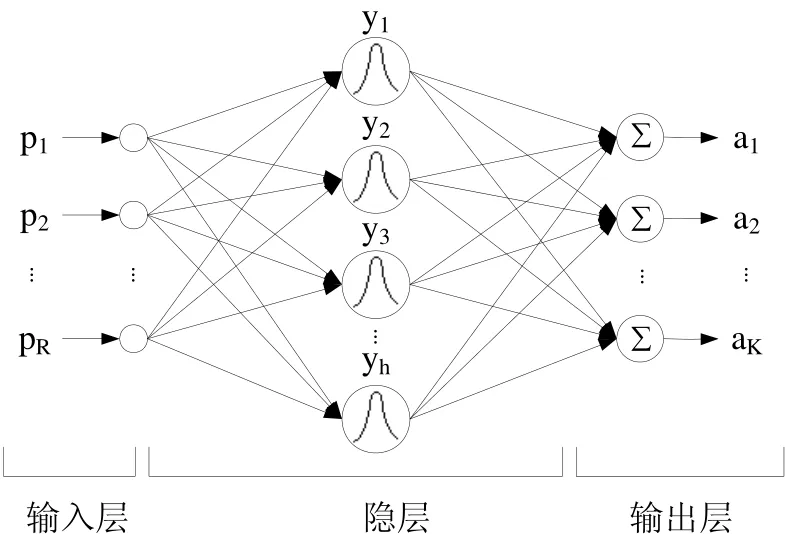
图2 径向基函数神经网络结构图

5 结束语

接触网可靠性研究是一项涉及面广而且复杂的系统工程，国内外有关铁路接触网系统可靠性研究也刚刚起步，任重而道远。目前接触网可靠性研究存在的问题和未来的研究方向主要有以下几方面：

（1）缺乏可靠性统计数据。

（2）关于铁路接触网系统各部件的内部应力与外部负载及环境因素的复杂的非线性关系，尚待研究。

（3）对各个部件主要失效模式进行机理分析和建立起相应的可靠度计算模型，估计出它们从开始工作到发生故障时间的可靠程度和工作寿命，并进行优化设计。

（4）综合权衡可靠性、维修性和经济性，使接触网系统各方面达到最优。

[1]张卫东，贺威俊.浅析我国高速铁路的发展进程[J].技术与市场，2011，18（5）：222-224.

[2]张卫东，贺威俊.电力牵引接触网系统可靠性模型研究[J].铁道学报，1993，（3）：31-38.

[3]冷宏俊.接触网系统可靠性分析与设计[M].北京：铁道科学研究院，1998.

[4]李群湛.系统可靠性原理[J].大连理工大学学报，1998，38（1）：81-85.

[5]孙德忠.提高接触网受电弓系统运行可靠性的研究[J].铁道机车车辆，1996，（3）：51-53.

[6]Kiyohiro. Reliability analysis of geometrically nonlinear structures with application to suspension bridges[D]. Dissertation Abstracts International, the university of Mi-chigan,1999.

[7]张建仁.结构可靠度理论及其在桥梁工程中的应用[M].北京：人民交通出版社，2003.

[8]张雷.基于神经网络技术的结构分析与优化设计[D].吉林：吉林大学，2004.

[9]赵国藩.工程结构可靠度理论与应用[M].大连：大连理工大学出版社，1996.

[10]于雷，郑云龙.基于改进Monte Carlo法的船体纵向弯曲强度可靠性分析[J].大连理工大学学报，1998，38（1）：81-85.