高速铁路雷击跳闸率的研究

2011-06-27郭小霞樊春雷

电气化铁道 2011年6期

关键词：闪络弧线避雷器

郭小霞，樊春雷

0 引言

目前国内对接触网防雷的研究非常少，并且没有统一的分析方法与应用措施。本文通过电气几何模型并利用暴露距离分别计算了牵引网系统中各导线遭受雷击的概率，并对线路采取避雷器保护后跳闸率进行了计算。计算结果为高速铁路防雷保护提供了重要的参考。

1 模型的建立

1.1 电气几何模型

电气几何模型（EGM）是指将雷电的放电特性与线路的几何结构尺寸联系建立起来的一种分析线路绕击的模型。在EGM中，关键概念是击距，导线和地面有各自相应的击距，雷电先导先到达哪一物体的击距范围内，即向该物体放电。因此可根据几何作图法作出各物体可能受雷击的范围。对于导线是以其轴线为圆心，击距为半径的圆弧；对于地面是一条高度为击距，平行于地面的直线。击距大小与先导头部电位有关，而后者又和主放电电流有关，因此认为击距是雷电流幅值的函数。除此之外，在电压等级较高时，还需考虑击距系数K（即先导对大地的击距与先导对导线的击距之比）。由于本文的电压等级低，因此，取击距系数为1。

1.2 高速铁路电气几何模型

本文研究高速铁路牵引网供电方式为 AT供电，牵引网由接触网，承力索及加强线构成，其中加强线布置在支柱顶端，而正馈线安装在支柱外侧，图1为高速铁路高架桥段复线牵引网电气几何模型。

图1 高速铁路高架桥段复线牵引网电气几何模型示意图

由于高速铁路接触网系统不像电力系统输电线路那样装有避雷线，因此，本文暂定雷电绕过加强线击于接触网或正馈线称为绕击，对应图中的弧线C2为加强线保护范围。对于某一数值的雷电流I，其相应的击距为rs，此时弧线C1和弧线C3为暴露在屏蔽范围外的弧线。当击距rs随雷电流的降低而减小时，暴露弧线C1和弧线C3将增大，绕击率也因此而增加，但与之相应的雷电流幅值低于接触网的耐雷水平I1时，即使雷击在接触网或正馈线上，闪络也不会发生。与I1相应的击距称为临界击距 rsc。当击距 rs随雷电流的升高而增大时，暴露弧线C1和弧线C3将逐渐减少，其中当暴露弧线C1与屏蔽弧线C2相交于中心线时，由于复线牵引网对称性接触网将完全被两侧加强线保护，此时，击距 r对应雷电流为最大接触网绕击雷电流Im1。对于暴露弧线C3，当弧线逐渐减少至0完全被加强线屏蔽，此时，击距称为最大击距rmax，与此对应的电流称为最大正馈线绕击雷电流Im2。

雷击接触网或加强线时，耐雷水平仿真结果为Ic= 3.85 kA[1]，对于暴露弧C1，最大绕击接触网雷电流Im1对应击距r通过式（1）可得：

高速铁路SOO'= 5.65 m，SEO''= 2.7 m，SO'O''=1.8 m；参数详见文献[1]。

由式（1）可得：r = 8 m。

本文采用IEEE推荐击距公式：

则由式（2）得：

通过式（3）可得：

即使接触网发生绕击，接触网绝缘子串也不会发生击穿。因此，在研究高速铁路高架桥段复线牵引网时，铁路侧接触网将完全被两侧加强线屏蔽不会发生绕击跳闸，故暴露弧C1在研究绕击跳闸率时不予考虑。

对于暴露弧C3，最大接触网雷电流Im2对应击距rmax通过文献[3]可得：rmax= 80 m。

根据式（3）可得：

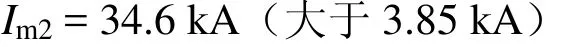
对于暴露弧C3，当雷电流幅值在[Ic，Im2]范围内时，正馈线绝缘子串将发生绝缘闪络。随着雷电流进一步增大，当Im2≤I≤100 kA时，击向牵引网的雷电将被加强线完全屏蔽掉。

综上，由于本文研究的高速铁路牵引网系统中加强线布置在支柱顶部。因此，本文重点研究：

（1）加强线未采取防雷保护措施时，牵引网跳闸次数公式推导及计算。

（2）加强线上安装避雷器后，牵引网跳闸次数公式推导及计算。以期对高速铁路雷击严重的高架桥段牵引网防雷保护措施实施提供重要的理论依据。

2 牵引网雷击跳闸公式推导

利用电气几何模型计算雷击跳闸次数，首先应确定以下参数：

（1）雷电流的概率密度f(I)。当对地闪络的雷电流幅值分布已知时，即可由雷电流幅值的分布得出其概率密度；当采用雷电流幅值对数概率分布为式（4）时，

式中，P(I)为幅值大于I的雷电流概率分布函数。

由f(I) = P′(I)，则雷电流概率密度：

由式（4）得雷电流小于 100 kA的概率为92.7%，结合实际，本文重点研究雷电流为100 kA以下的雷电对牵引网跳闸次数的影响。

（2）地面落雷密度Ng。计算年落雷次数，本文采用国际大电网会议推荐的公式计算。

（3）牵引网雷击闪络跳闸率Pα。根据暴露距离的物理概念，可以得到整段高速铁路高架桥段复线牵引网雷击跳闸率面积为 2×L×DS，L为线路长度，km，DS为导线的暴露距离，m，则

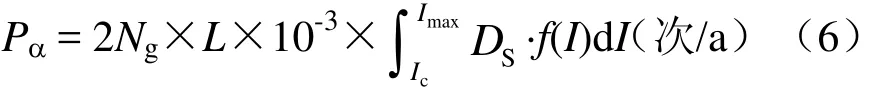
2.1 未采取防雷保护措施时牵引网跳闸率

雷击牵引网的跳闸分别为雷击加强线跳闸和雷击正馈线跳闸。

计算过程如下：首先，建立坐标系XOY，以加强线所在点作为坐标系的原点O，正馈线所在点坐标为C，以地面平行的过原点的直线为X轴，垂直于地面的直线为Y轴。设A点坐标为A（xa，ya），B（xb，yb），C（xc，yc），DZ1对应暴露弧 C2，DZ2对应暴露弧C3（见图2）。

此时，A点的坐标为

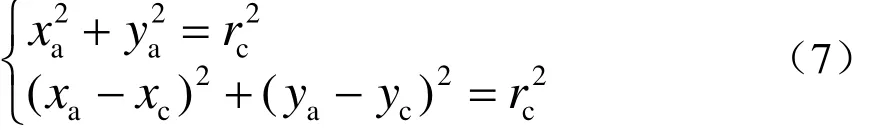
B点的坐标为

则

代入式（6）可分别计算出雷击加强线和雷击正馈线的发生绝缘闪络的概率。

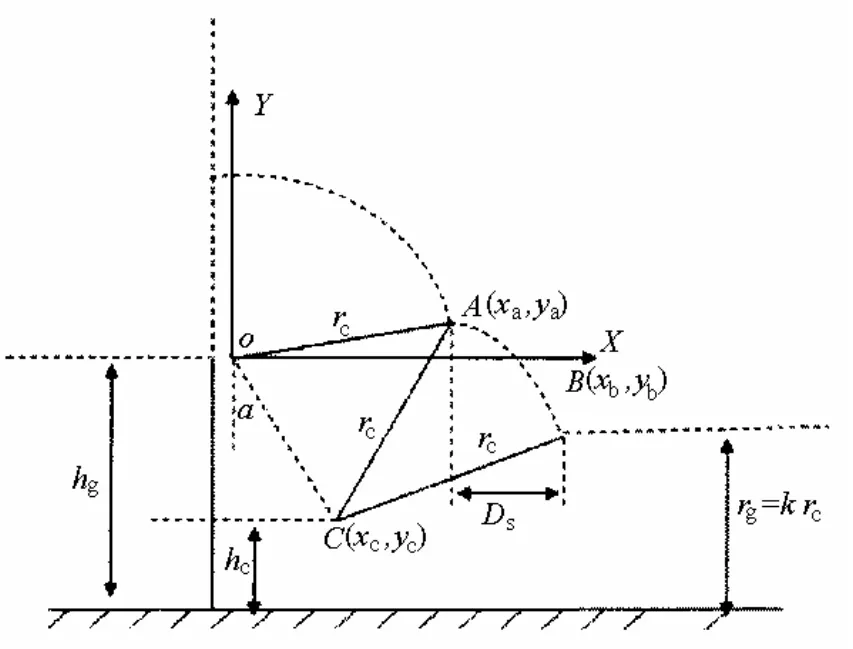
图2 电气几何模型图

2.2 加强线采用避雷器保护时牵引网跳闸率

根据文献[1]仿真结果，在加强线绝缘子两端并联1支避雷器时，对应的耐雷水平Ip= 65.5 kA。因此，当雷电流小于65.5 kA时，即使发生雷击加强线，加强线绝缘子串也不会发生绝缘闪络。同时，通过研究发现当雷电流大于34.6 kA时，正馈线将完全被加强线保护，此时，击向牵引网的雷电将完全被加强线屏蔽。综上，当加强线采用避雷器保护后，其闪络概率计算如式（10）：

代入式（6）可分别计算出雷击加强线和雷击正馈线的发生绝缘闪络的概率。

3 计算实例

本文研究的高速铁路全线桥梁占线路全长的80%，桥梁高度为11.6 m，加强线离桥梁的平均高度为8.7 m，接触网离桥梁平均高度为5.3 m，正馈线离桥梁平均高度为 7.39 m。加强线分别与接触网、正馈线的水平间距为3.15 m和1.5 m。

本文分别对牵引网系统中加强线采用避雷器前后牵引网雷击跳闸率进行了计算，结果显示，当所研究的高速铁路高架桥段线路长度为100 km，且沿线最大雷电流幅值达到100 kA时，未采取防雷保护措施下发生雷击正馈线绝缘闪络的次数1.96次，而发生雷击加强线绝缘闪络次数高达 23次，远远高于雷击正馈线的情况。当加强线两端并联1支避雷器后，发生绝缘闪络的次数降低为5.56次，比未安装避雷器时降低了75.8%，研究发现加强线是否安装避雷器对正馈线闪络次数没有影响。