三维离散纵标方法在RPV快中子注量率计算中的初步应用

杨寿海，陈义学，王伟金，石生春，陆道纲

（华北电力大学核科学与工程学院，北京102206）

压力容器是反应堆的不可更换构件，压力容器的寿命是由压力容器材料的脆化程度和加压热冲击程度决定的，而快中子辐照脆化是限制RPV寿命的最重要的性能劣化机理，因此必须要准确计算RPV处的快中子注量率分布。由于离散纵标方法［1］在解决“深穿透”问题方面的突出优势，在过去的几十年内它一直是计算压力容器快中子注量率的主流方法［2－3］之一，同时在RPV快中子注量计算中MCNP程序也越来越多地受到关注［4］。但是受计算机内存容量及计算速度的限制，同时三维离散纵标方法本身的不完善，前人在压力容器快中子注量率计算中大多采用一维、二维离散纵标方法，并用一维与二维方法合成三维分布，由于引入了较多的近似，因此合成的三维计算结果精度有待提高。随着计算机内存容量及计算速度的飞速发展，同时三维算法及三维辅助工具的开发，使得三维离散纵标方法应用于反应堆的设计计算中成为现实的可能［5］。本工作针对TORT程序在大型压水堆中的应用分析，开展探索性的尝试，并与常用的Monte Carlo方法及二维离散纵标法进行了比较。堆芯计算采用全堆芯三维中子学程序SCIENCE软件包，堆芯外输运计算采用TORT程序。

1 程序与截面库及验证

1．1 程序与截面库

离散纵标方法（即SN方法）最早是由卡尔逊及拉舍尔等人提出的，它以确定论方法求解输运方程。目前国内屏蔽计算主要采用一维离散纵标法程序ANISN和二维离散纵标法程序DOT［3］，并用一维与二维方法得到的结果合成三维注量，由此得到的三维计算结果理论的可信度不高。

本工作采用国际通用的三维离散纵标法程序TORT［6］程序，该程序由美国橡树岭国家实验室开发，能准确、详细地给出二维、三维中子与γ射线的空间分布，同时具有进行keff、固定源、临界浓度及临界尺寸搜索等强大功能，尤其适合于解决“深穿透”辐射屏蔽问题。

TORT程序使用基于核评价数据库ENDF／B－VI开发的MATXS格式的通用多群截面数据库，该数据库是一个30n×12g、300K、P4阶展开、包含121种核素的中子、光子及中子光子耦合的多群截面数据库。

1．2 程序验证

国际上已经将该程序应用于VENUS－3的压力容器快中子注量计算的工程实践中［7］，同时进行了大量的基准验证［8－9］，初步证明了该程序在核反应堆压力容器快中子计算中应用的可行性与可靠性。TORT程序在国内核工程中的应用分析尚处于起步阶段，为了验证其工程可靠性及准确性，作者及其所在研究所针对NUREG／CR－6453基准题，分别采用TORT、MCNP［10］和DORT等程序进行计算，得到了辐照监督管处典型核素的计算活度值与测量活度值之比（C／M），如表1所示，详细的计算模型及计算参数见文献［2，11－12］。

表1 计算与测量活度之比（C／M）Table 1 Ratios of calculated－to－measured specific activities（C／M）

计算结果表明三个程序及其对应的截面库计算结果与测量值吻合较好；MCNP程序和TORT程序的计算结果精度均高于DORT程序合成的结果。

2 计算模型

2．1 堆芯计算模型

本工作以某压水堆为例，进行三维建模，堆芯由内至外依次围绕有堆芯围板、反射层、吊篮、第一下降区、热屏、第二下降区、压力容器、保温层、空腔室。燃料组件的尺寸21．504cm×21．504cm，17×17的棒孔，活性区高度为365．67cm。堆芯是由157个燃耗深度不同的燃料组件组成的，燃料组件的初始富集度为4．45%，每个组件中含有264根燃料棒、24根控制棒和1根通量测量棒。为了降低压力容器的快中子注量率，十种不同类型及不同燃耗深度的燃料组件在堆芯内交叉布置，并将组件中放入含钆棒，钆棒数目分别为0、8、20、24根。计算时采用单组件均匀化，堆芯围板、吊篮、热屏、压力容器内堆焊层均为密度7．92g／cm3的SS316合金钢，压力容器采用密度7．85g／cm3的A508－Ⅲ碳钢，考虑到反应堆的对称性，只计算了八分之一堆芯尺寸，各区具体的尺寸、材料参见图1与图2，为了更精确地描述堆芯不同位置功率的变化，将堆芯组件区域划分为10类组件，轴向划分为16段计算了不同位置的裂变中子源强。

图1 压水堆三维模型图（1／8）Fig．1 3－D model for PWR（one octant）

该反应堆模型平衡循环的平均温度约为315℃，下降区的平均温度约为298℃，循环平均压力为15．513MPa，冷却剂中循环平均硼浓度为500×10－6。

2．2 计算过程及参数选取

图2 压水堆三维模型水平剖面图（1／8）Fig．2 Horizontal cut of 3－D model for PWR（one octant）

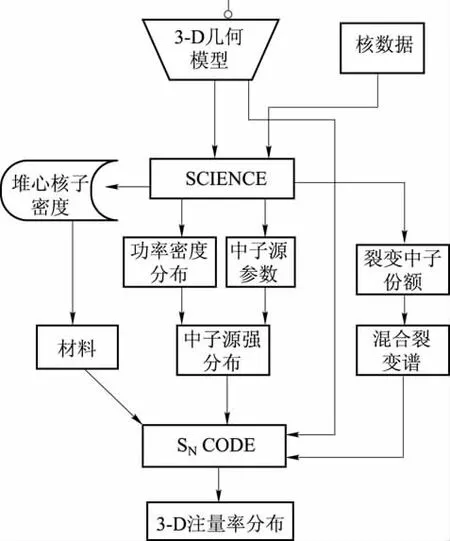
图3 压力容器快中子注量率计算流程图Fig．3 Processing of RPV fast neutron flux calculation

压力容器快中子注量率计算流程如图3所示。由于随着燃耗的加深堆芯不同裂变核素的裂变份额不断变化，而且不同裂变核素每次裂变放出的中子数、裂变能都不尽相同，所以采用全堆芯三维中子学程序SCIENCE软件包计算与燃耗相关的参数，得到考虑组件燃耗深度后的材料密度、中子源强和裂变能谱。堆芯裂变源强由堆芯的功率密度相对分布通过式（1）计算得到。

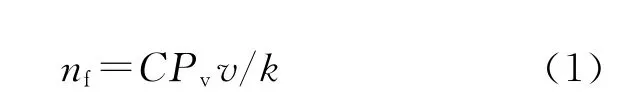
其中：nf—裂变中子源归一化因子，1／（cm3·s）；C—能量换算因子，C＝6．241 46×1 012MeV／J；Pv—组件或燃料棒的功率密度，W／cm3；v／k—释放单位裂变能量对应的裂变中子数，n／MeV。

由于238U、239Pu、240Pu、241Pu的裂变谱较235U相比更硬，中子穿透能力更强，且压力容器快中子注量主要受外围组件的影响，所以根据双群堆芯外围组件不同裂变核素的裂变中子份额，制作了堆芯外围组件混合裂变谱并作为SN程序的源裂变能谱。

计算中严格参照美国NRC公布的计算导则RG1．190，使用R－θ－Z三维几何模型，为了方便结果对比，采用组件均匀化模型，在R、θ和Z三个方向分别划分的网格数为94、53和106，网格总数为528 092个。计算截面参数采用P3阶勒让德展开式，选用S8阶高斯全对称求积组近似求解。计算点通量收敛迭代标准设为5×10－5，采用固定源模式在奔腾III个人计算机上的CPU计算时间为1 863min。当对网格继续细化时计算结果的偏差不超过1．5%；当提高勒让德展开阶数及增加求积组系数时，计算结果的变化均小于0．5%。

3 计算结果与分析

3．1 中子注量率

由于反应堆的设计寿命主要取决于压力容器的寿命，因此要精确的计算反应堆寿期内压力容器内壁及距内壁1／4厚度处的快中子注量值。通过三维程序的后处理模块得到堆芯中平面快中子（E＞1MeV）分布图4和0°角位置快中子注量率垂直分布图5。

3．2 结果比较

本工作过程中采用了单组件的均匀化处理，应用三维的R－θ－Z模型求解三维输运模型进行三维RPV计算分析，而过去的离散纵标计算中多采用通量密度合成法，即：

式中：Φ（R，θ）表示R－θ几何模型对应的中子注量率；Φ（R，Z）表示R－Z几何模型对应的二维中子注量率；Φ（R）表示一维柱模型中子注量率。

图4 快中子水平分布图Fig．4 Horizontal distribution of fast neutron

图5 快中子垂直分布图Fig．5 Vertical distribution of fast neutron

采用（2）式将一维与二维离散纵标方法计算的结果合成三维快中子（E＞1．0MeV，E＞0．1MeV）注量率分布；同时使用MCNP程序及基于ENDF／B－Ⅵ的连续截面数据库对2．1节模型进行计算，采用片层计数方式，运行2 400min后抽样的粒子数为67 907 014个，最大统计偏差小于2．7%，满足收敛标准，得到压力容器内壁处快中子（E＞1．0MeV，E＞0．1MeV）注量率环向分布。最终将三维离散纵标方法得到的压力容器处快中子（E＞1．0MeV，E＞0．1MeV）注量率分别与低维合成的结果及MCNP程序计算结果相比较如图6所示。从图中可以看出三种方法得到的压力容快中子注量率结果差别较小，趋势一致。三维离散纵标方法的计算结果介于较一维、二维SN合成结果与MCNP的结果之间，误差在工程可接受范围内。分析原因可能有：1）由于3－D SN模型较一维、二维SN对几何描述的更准确，且没有合成过程，减少了模型简化近似引入的偏差因而更可信；2）MCNP程序由于方法本身较SN方法理论上更精确，且MCNP程序使用的是基于ENDF／B－Ⅵ的连续截面数据库而SN方法使用的是基于ENDF／B－Ⅵ的多群截面数据库，所以会引入一部分不确定度导致偏差产生。

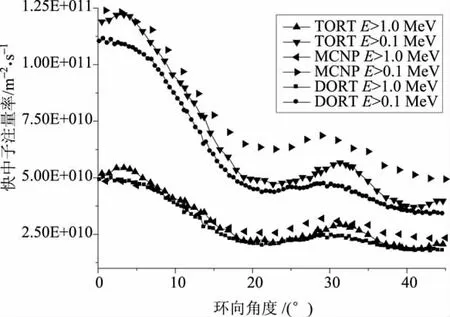
图6 不同方法得到的压力容器内壁快中子注量率环向分布对比Fig．6 Comparison of RPV fast neutron obtain by different approaches

4 结论

本工作采用三维离散纵标法程序TORT及多群截面库对某压水堆进行三维压力容器快中子注量计算分析，并与传统的一维、二维通量合成方法结果及MCNP方法的结果进行比较，结果表明：三维离散纵标方法的较精度要高于传统的通量合成的方法，与MCNP结果的偏差在工程可接受范围内，TORT程序在压力容器注量计算中是适用的；同时也展示了三维算法在几何建模和结果后处理方面的强大功能。对三维离散纵标方法程序应用于压水堆的压力容器快中子注量计算进行了初步的尝试。

［1］ B G Carlson，G I Bell．Solution of the Transport Equation by the SN Method［R］．Proc N Intern Con ＆Peaceful Uses At Energy，2nd，Geneva P／2386，1958．

［2］ M L Williams，M Asgari，F B K Kam．Impact of ENDF／B－VI Cross－Section Data on H B Robinson Cycle 9Dosimetry Calculations［R／OL］．NUREG／CR－6071，October 1993．

［3］ 傅守信，胡建军．秦山核电二期工程反应堆主屏蔽设计［J］．核动力工程，2003：64－68．

［4］ U．S．Nuclear Regulatory Commission．PWR and BWR Pressure Vessel Fluence Calculation Benchmark Problems and Solutions［R／OL］．USA：brookhaven national laboratory，NUREG／CR－6115，2001．

［5］ Enrico BOTTA，Roberto ORSI et al．Westinghouse AP1000Internals Heating Rate Distribution Calculation Using a 3DDeterministic Transport Method［C］．13th International Conference on Nuclear Engineering，China，2005．

［6］ W A Rhoades，et al．TORT－DORT Two－and Three－Dimensional Discrete Ordinates Transport Version 2．8．14［P］．USA：Oak Ridge National Laboratory，1994．

［7］ M PESCARINI，et al．ENEA Nuclear Data Centre Neutron Transport Analysis of the VENUS－3Shielding Benchmark Experiment［R］．KT－SCG－00013，ENEABologna，Italy，2001．

［8］ CHIKARA KONNO．TORT Solutions with FNSUNCL3for KOBAYASHI'S 3DBenchmarks［J］．Progress in Nuclear Energy，2001，39（2）：167－179．［9］ Kursat B Bekar a，Yousry Y Azmy．TORT solutions to the NEA suite of benchmarks for 3Dtransport methods and codes over a range in parameter space［J］．Annals of Nuclear Energy，11，2008．

［10］ MCNP4CMonte Carlo N－Particle Transport Code System［CP］．Contributed by Los Alamos National Laboratory，2000．

［11］ 杨寿海，陈义学，王伟金，等．三维离散纵标方法在堆内构件释热率计算中的初步应用［J］．核动力工程，2011．

［12］ 石生春．基于蒙特卡罗方法的压水堆压力容器快中子注量率的计算分析［D］．北京：华北电力大学，2010．