基于自适应遗传算法和蚁群算法融合的配电网重构

张明光 赵金亮 王维洲 张彦凯 路染妮 李正元

(1.兰州理工大学 电气工程与信息工程学院，甘肃 兰州 730050;2.甘肃电力科学研究院，甘肃 兰州 730050)

0 引言

配电网具有闭环设计、开环运行的特点，根据负荷的不同情况调整配电系统中的开关的开合状态，称之为配电网重构。重构后的网络结构既可以在很大程度上降低线路损耗，又能均衡馈线之间的负荷。所以配电网重构是提高配电系统经济性和安全性的重要途径［1］。在电能的输送和分配过程中，配电网的网损占了整个电网网损相当大的比例，这就确定了配电网重构的必要性。

配电网络重构是一个大规模非线性混合规划问题，具有大量的局部最优解，一般不可微、不连续、多维、有约束条件、高度非线化等特点［2］。如何进行全局最优化，正是本文要做的工作。

1 数学模型

1.1 配电网重构的以线损最小为目标函数的数学模型

配电网络重构影响配电网的线损，所以线损最小的目标函数为

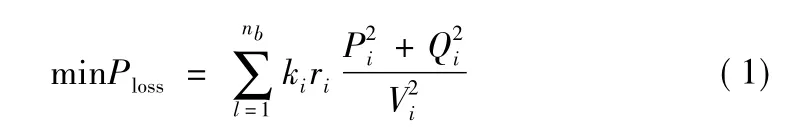
式中:ri第i条弧的电阻;

Pi，Qi支路i的有功功率和无功功率;

Vi支路i末端的节点电压;

Ki开关i的状态变量，是0-l离散量;

0代表打开，1代表闭合。配电网线损:

Ploss可以通过潮流计算得到。

约束条件为

(1)配电网重构必须满足潮流方程。

(2)支路电流及节点电压约束

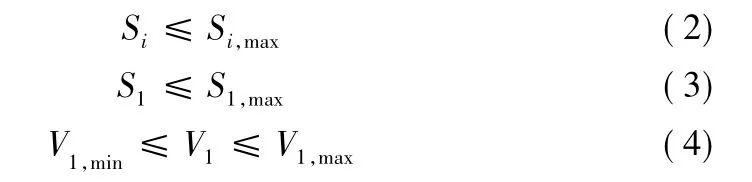
式中

SiSi，max各支路i流过的功率计算值及其最大容许值;

S1S1，max分别为变压器的供出功率及其最大容许值;

V1，min和 V1，max: 节点 i的电压上限和下限值。

(3)网络结构约束:重构后的配电网必须为辐射状。

(4)供电约束:所有负荷都有电源，不能存在孤立节点。

1.2 配电网重构的电压质量目标函数的数学模型

毕鹏翔等在文献［3］中提出将电压平衡指数作为配电网重构电压质量的目标函数，TSij表示节点i和节点j之间的联络开关，因此设环路中联络开关TSij处的电压平衡指数VBLij为

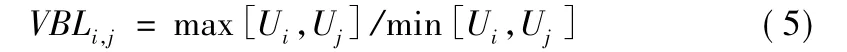
max［Ui，Uj］表示取其大者，min［Ui，Uj］表示取其小者，由此得到提高电压质量的目标函数为

α为联络开关TSij两端的节点。

2 配网重构的自适应遗传算法和蚁群算法融合

自适应遗传算法和蚁群算法融合算法［4］初期采用遗传算法利用快速全局搜索能力强求得初始解，利用这些解生成蚁群算法的信息素分布，后期利用蚁群算法的正反馈机制求得精确解。进而形成时间效率和精确解效率兼得的一种新的智能算法。利用种群相似度来找到融合算法的最佳融合点:通过实验获得本文融合算法最佳融合点的种群相似度的差值，当所求差值小于该差值时停止迭代。即在遗传算法求最优解效率降低的时候能停止，进而使用求最优解效率较高的蚁群算法。

3 算法的具体实现

GAACA(遗传蚁群混合算法)中的遗传算法规则见文献［5］。

3.1 染色体编码

通过对配电网的简化分析，确定出有些开关必须闭合，否则形成孤岛等。将剩余的开关状态按编号顺序一次用0(开)或1(合)表示，即形成一条染色体。编号的开关数作为一条染色体的长度。

3.2 适应度函数的设计

遗传算法在进化搜索中基本不利用外部信息，仅以适应度函数为依据，适应度函数值越大说明该个体越好。因此，以各支路上的有功损耗的总和的倒数为适应度函数

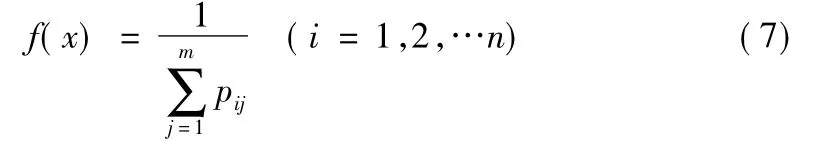
其中pij每条支路上的有功损耗。

3.3 选择方式

每次从群体中随机选取两个个体进行适应度函数值比较，值较大的保留。若相等，任选一个保留。

3.4 自适应交叉算子

如文献［6］文献［7］提出的方法都是交叉率随适应度函数值自适应变化，这样使遗传算法能保持较强的搜索能力。但是人为因素重，难跳出这个局部最优解等。

因此，在初期采用较小交叉率，使个体在自己所在区域附近进行小范围搜索，使群体收敛到最优解，无论得到局部最优解还是全局最优解。此时再加大交叉率，使陷入局部最优解的个体跳出局部最优;因为采用了最优个体保留策略，将不影响全局最优的个体。这样既保证了算法的快速收敛，又避免了早熟早收敛。此种交叉率随最优个体保持代数双曲线上升，有下式决定

图1 自适应遗传算法和蚁群算法融合的流程图

Pcmax:最大交叉率(这里取1.0)。

Pcmin:最小交叉率(这里取0.5)。

m:最优个体已经保持的代数。

Mmax:遗传算法指定的最优个体最少代数。

按适应度函数值对个体进行由大到小的降序排列，保留前半部分个体［8］，生成新的种群。

3.5 变异算子

文献［6］发现变异率随着遗传代数指数下降的效果最好，因此在本文中也采用指数函数，公式如下所示

Pmmax:最大变异率(这里取0.45)。

Pmmin:最小变异率(这里取0.01)。

λ:常数(这里取λ=10)。

m:最优个体已经保持的代数。

Mmax:遗传算法指定的最优个体最少代数。

3.6 迭代终止条件的确定

利用染色体相似度和种群相似度的差值来停止遗传算法的迭代

定义1 染色体相似度σ=p/q，其中p为两个不同染色体中相同基因的个数，q为两个染色体中的基因总数［9］。

定义2 种群相似度K为

其中i为任意个体，j为最优个体，σi为个体i的染色体适应度函数值与最优个体j的染色体适应度函数值的差值，即σi=fj-fi，n为种群中的个体总数。任意两代K的差值ΔK越大，表明种群进化越慢;ΔK值越小，表明种群进化越快。当遗传算法迭代效率降低时对应的相邻两代的ΔK为两种算法最佳融合的值。我们用简单的实验选取ΔK值，测试数据见表1。

表1 ΔK值的参数选择表

实验结果表明，当ΔK=0.15时使得GAACA在求解效率和迭代次数上都达到最优，因此本文取ΔK为0.15。

4 蚁群算法操作

本文使用蚁群算法来解决配电网网络重构问题，该算法避免了辐射型检查过程，只搜索可行解区域。

4.1 搜索策略

4.2 信息素更新原则

本文算法的信息素更新分为两个部分［10］:第一部分，利用遗传算法生成的较优个体调整信息素的初始分布，公式如下

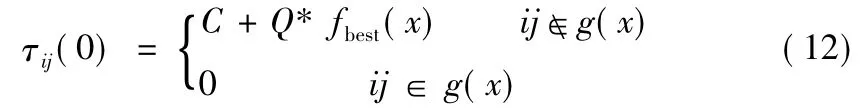
式中:C、Q为常数，fbest(x)和g(x)分别为第x个较优个体的适应度函数值和断开的支路集合。每次迭代后的信息素根据值确定的当前种群较优个体来更新，信息素调整如式(13)

第二部分:蚂蚁搜索过程中的局部信息素更新。蚂蚁每走完一条配电网支路，根据式(14)调整配电网支路上的信息素

式中:t为代数;ρ为信息素衰减系数，表示信息素随时间的消逝程度;Q为常数，f(x)为第x个个体的适应度函数值。其中，Δτij(t，t+n)表示本次搜索路径(i，j)上信息素的增量，通常设置ρ＜1来避免路径上信息素的无限累加。本文根据配电网的实际将适应度函数进行了改进，将支路电阻考虑进来，实验仿真证明结果优于未改进时的结果。

5 算例及分析

本算例采用上图所示的美国PG＆E额定电压为12.66 kV，总负荷为3 802 kW+j2694kvar，准功率:100 MVA，基准电压:12.66 kV。参数设置为染色体长度为57，种群数为30。

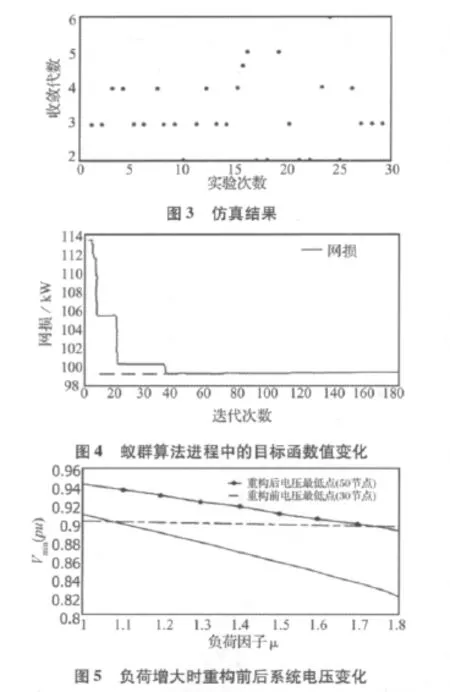
进行30次实验，每次都能求解到最优解，由图3可以看出，一般在第3～5代收敛，可见本文采用的方法既能提高计算速度，又能求得精确解。

图4表明在n=39代时，目标函数值保持不变，各条支路上信息素也不再更新，说明最优解已经找到。输出结果如表 2所示。

图5反映了重构前后系统的负荷裕度。重构前，当负荷为原负荷的1.1倍时，46节点电压已低于最低电压0.9(p.u.)。而重构后在负荷为原负荷的1.6倍时，配电网仍然可以正常运行［11］。

表2

图2 美国PG＆E69节点配电系统(重构前)

对于同样的算例:文献［12］采用模糊遗传算法，染色体长度为74，取初始种群为100，初始交叉概率为0.9，初始变异概率为0.01，在迭代到300代时得到最优解。文献［13］采用改进遗传算法，染色体长度为59，取初始种群为50，初始交叉概率为0.9，初始变异概率为0.01，在迭代到21代时得到最优解。可见本文的方法提高了收敛速度。

［1］张大海，江世芳，赵建国.配电网重构研究的现状与展望［J］.电力自动化设备，2002，22(2):75-76，82.

［2］胡敏佑，陈元.配电系统最优网络重构的模拟退火算法［J］.电力系统自动化，1994，18(02):24-28.

［3］刘健，毕鹏翔，董海鹏.复杂配电网简化分析与优化［M］.北京:中国电力出版社，2002.

［4］刘自发，葛少云，余贻鑫.一种混合智能算法在配电网络重构中的应用［J］.中国电机工程学报，2005，25(15):73-78.

［5］Baran M E，Wu F F.Optimal Capacitor Placement on Radial Distribution Systems［J］.IEEE Trans on Power Delivery，1989，4(1):725-734.

［6］袁慧梅.具有自适应交换率和变异率的遗传算法［J］.首都师范大学学报(自然科学版)，2000，21(3):14-20.

［7］卢耀武.基于自适应遗传算法的配电网络重构［J］.华中电力，2005 18(6):16-18.

［8］李晓明，黄彦浩，尹项根.基于改良策略的配电网重构遗传算法［J］.中国电机工程学报，2004，24(2):495-498.

［9］彭建，于晓翠.基于遗传算法与蚁群算法动态融合的网格任务调度［J］.计算机应用与软件，2009，(7)121-123，80.

［10］李德华，等.模糊遗传算法和蚁群算法相结合的配电网络重构电力系统保护与控制，2009，(9);26-31.

［11］姚李孝，任艳楠，等.基于蚁群算法的配电网网络重构电力系统及其自动化学报，2007，(12):35-39.

［12］刘莉，陈学允.基于模糊遗传算法的配电网络重构［J］.中国电机工程学报，2000.20(2):67-70.

［13］毕鹏翔，刘健，等.配电网络重构的改进遗传算法［J］.电力系统自动化，2002，25(1):57-61.