复杂金融系统的重现时间间隔分析
2011-06-23顾高峰蒋志强周炜星
任 飞, 顾高峰, 蒋志强, 周炜星
(华东理工大学商学院,上海 200237)
复杂金融系统的重现时间间隔分析
任 飞, 顾高峰, 蒋志强, 周炜星
(华东理工大学商学院,上海 200237)
依据复杂性科学的思路,研究了金融市场大波动极端事件的重现时间间隔,考察了中国股市高频数据的重现时间间隔分布和时间关联特性,介绍了几种分布检验和关联测度方法,从不同角度进行精确分析.其次,系统介绍了重现时间间隔分析方法在金融复杂系统研究中的应用,对波动率、已实现波动率、收益率和交易量的重现时间间隔进行了实证分析,并在此基础上进行初步市场风险估计.最后,介绍了基于委托驱动的微观模型,通过模拟交易人的委托下单过程模拟市场的价格波动演化,研究大波动极端事件重现时间间隔的动力学机理,为中国股市大波动极端事件的风险估计和规避提供理论依据.
金融物理学;极端事件;重现时间间隔分析;金融风险
近年来我国经历了暴雪、地震、干旱、金融危机等一系列事件,这些异常的、平时不易发生的事件在统计学意义上称为极端事件.肇始于美国次贷危机的全球金融危机,被认为是1929年美国股灾后近百年来最严重的金融危机,当前面临的欧洲债务危机,也可能导致世界经济的再次探底.研究金融极端事件的统计规律和内在动力学机制,对估计金融市场风险并采取措施规避风险有着十分重要的意义.传统经济学理论框架建立在有效市场假设的基础之上,无法解释和预言此次金融危机.当前面临的经济困境促使科学家重新审视主流经济学理论,著名物理学家Bouchaud和经济学家Lux和Westerhoff分别在《Nature》和《Nature Physics》上发表评论,指出现有的经济理论需要根本性的科学革命,应该从实验金融数据出发归纳总结金融市场自身的运动规律[1],以解决目前的金融危机问题[2].
金融复杂系统具有和自然界复杂系统十分类似的特征行为,受此启发人们运用复杂性科学、非线性科学和计算实验科学等自然科学的方法来对其进行研究[3-6].金融市场内伴随某个大波动极端事件,紧接着发生一系列后续波动,同多粒子体系的自组织临界现象非常相似.诱发后续波动的大波动极端事件决定了金融市场的动力学行为及其复杂性,直接反映了市场的风险水平,采用重现时间间隔的分析方法研究大波动,能为金融市场的风险管理提供新的视角和思路.
1 基本概念、方法、理论结果
重现时间间隔(recurrence interval)定义为某个连续事件之间的时间间隔,早期集中在对自然界极端事件的研究中,比如洪水、高温天气和地震等自然灾害[7-9].金融极端大波动事件的重现时间间隔研究已经引起了许多学者的关注[10-16].股票价格的波动率或收益率连续地超过某个阈值q的大波动事件间的时间间隔,简称为重现时间间隔τ.可根据重现时间间隔的概率分布特征,由较大阈值的时间间隔分布推理得到极端大波动事件的时间间隔分布规律,能克服极端大波动统计样本不足的困难,对于金融市场的风险估计和管理具有现实意义.进一步的实证和模拟研究表明,重现时间间隔的这种标度行为可能产生于原始记录的长期记忆效应(longterm memory)[12-15].
关于大波动重现时间间隔的分布形式还没有统一定论.早期大波动的重现间隔时间分布研究主要是基于概率分布的定性观测.Yamasaki等[10]首次运用重现时间间隔的分析方法研究股票的波动率,采用美国股市的日度数据,将波动率简单定义为对数收益的绝对值,发现波动率重现时间间隔的概率密度具有标度行为(scaling behavior).Wang等[11]采用美国股市的日内高频数据,证实了波动率重现时间间隔分布的标度行为,其具体分布形式遵从拉伸指数分布(stretched exponential distribution),Jung 等[16]在日本股市中也观测到类似的拉伸指数分布.
随着研究深入到对高频数据的分析,一系列高精度的定量分析方法被引入,例如KS(kolmogorovsmirnov)检验方法、m-阶矩测量、基于bootstrap方法的KS拟合度检验等.Wang等[17]采用纽约证交所的逐笔交易与报价数据,通过测量τ/<τ>的m-阶矩,发现间隔时间的分布略微偏离标度律,类似的偏离标度律行为在韩国股市中也被观测到[18].Bogachev等[19]也发现重现间隔时间的分布随阈值q变化,且分布形式遵循幂律分布.
具有多体相互作用的复杂体系具有长程时间关联(也称为记忆效应),是构造极端事件的重现间隔时间分布模型的主要依据.经验数据研究表明,极端事件的间隔时间分布与波动率的长程关联密切相关[12-15],根据这一机理,构造了一系列微观动力学模型.用傅立叶变换构造具有分形和线性长程关联特性的时间序列,其间隔时间分布具有标度行为,且分布服从拉升指数分布[4,20],其解析解近似可解[12-13].用多重分形随机行走模型,构造具有多重分形和长程关联特性的时间序列,无论关联为线性或非线性,间隔时间分布都无标度行为,但分布遵循幂律分布[19,21].
目前,中国股市波动的重现时间间隔研究还比较少.Qiu等[22]采用比较直观的方法观测上交所4只股票波动率的重现时间间隔的概率分布,认为重现时间间隔的分布具有标度行为,且标度函数服从拉伸指数分布.Ren等[23]分析上交所和深交所30只交易活跃的股票两年的日内高频数据,采用m-阶矩测量方法考察波动率重现时间间隔分布的标度行为,发现大多数股票的时间间隔分布偏离标度律,并采用基于bootstrap方法的KS拟合优度检验证实标度函数遵循拉升指数分布.最近,Ren等[24]采用20只在上交所和深交所上市股票的将近10年的日内数据,发现收益率的重现时间间隔分布遵循幂律分布,类似结果在交易量的重现时间间隔分析中也被观测到[25-26].
1.1 定义
假设有某一股票的时间序列,根据该时间序列可以求得原始变量R(t),R(t)可以是波动率、收益率等任一变量.在数据预处理阶段需要对R(t)进行归一化处理(normalization)
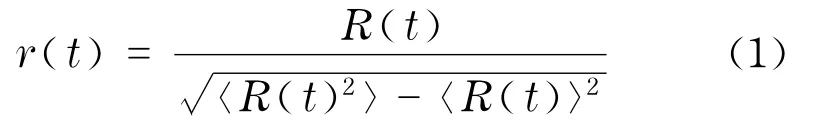
归一化变量r(t)的重现时间间隔定义为该变量连续地超过某个阈q的时间间隔,用字母τ表示.图1所示的是归一化变量r(t)的重现时间间隔的示意图,对应波动率和交易量的归一化变量,τ为由q>0的阈值截取的时间间隔,对于收益率的归一化变量,由于收益率可正可负,τ为由q>0和q<0截取的时间间隔.每取一个阈值q,便可得到阈值下的一组间隔时间序列τ.可通过观测不同阈值下的重现时间间隔,研究这些超过阈值q的事件重现的规律.
1.2 分布及检验方法
经验研究发现重现时间间隔的概率分布可能满足拉伸指数分布、幂律分布或者两者的混合分布,因此需要采用相对精确的拟合和拟合优度检验方法来确定具体的分布形式.常用的拟合方法是由Newman[27]提出的基于KS统计量的极大似然估计方法,该方法最早是针对幂律分布的拟合提出的,但该方法对于其它分布的拟合也有较好的适用性.
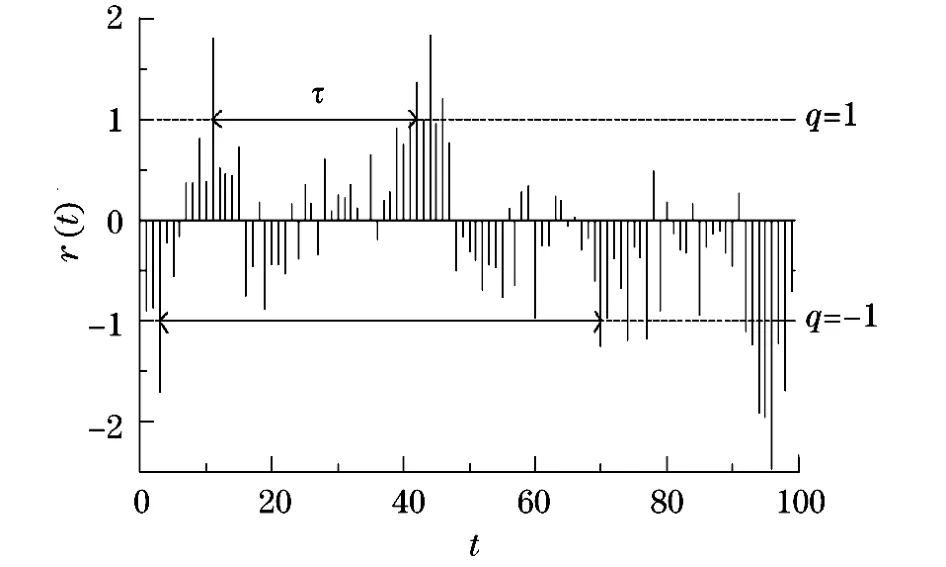
图1 归一化变量r(t)的重现时间间隔的示意图Fig.1 Illustration of recurrence intervals of the normalized returns r(t)
某个变量x的概率密度函数为P(x),其累积概率分布函数为F(x),假设变量x大于x^min部分满足某个理论分布,该理论分布的累积概率分布函数为Ffit(x),则KS统计量定义为
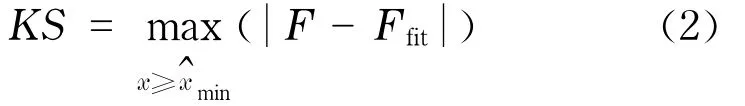
为了使得拟合的理论分布更接近于变量x的实际分布,KS统计量应该尽量的小.值在KS统计量取最小值求得,拟合分布的参数由极大似然估计解得.
对于已知分布的检验,可采用基于bootstrap方法的KS拟合优度检验,用来检验实证数据是否服从拟合得到的理论分布.前面已经求得变量x的实证数据的KS统计量,我们还可以计算加权的KS统计量
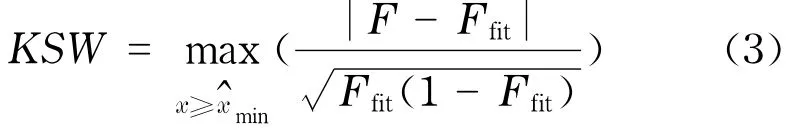
加权的KS统计量KSW在累积概率密度函数的边缘会更敏感.
接下来采用bootstrap方法随机产生1 000组模拟数据,模拟数据的概率分布满足拟合得到的理论分布,且模拟数据的数量等于变量x的实证数据的样本数.对每一组生成的模拟数据重构其累积分布函数Fsim,并且采用Newman等人的方法对模拟数据进行拟合,计算相应的累积分布函数Fsim,fit.对这1 000组模拟数据计算其KS统计量和KSW统计量
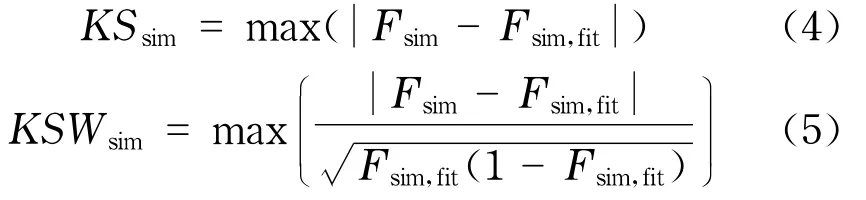
KS拟合优度检验的p- value由实证数据的KS(或KSW)统计量和模拟数据的KSsim(或KSWsim)统计量比较生成,定义为KSsim>KS(或KSWsim>KSW)的概率.p- value可以解释为实证数据的分布与拟合得到的理论分布的累积概率分布函数差值小于随机误差(随机数据的累积概率分布函数差值)的概率,也可以理解为实证数据分布服从于拟合分布的概率.这样就可以通过p- value来描述拟合得到的理论分布的拟合优度.在显著水平为5%的条件下,若p- value大于5%,则原假设被接受,我们就可以说重现时间间隔的分布能很好地被理论分布拟合;若p- value小于5%,那么拒绝原假设,说明重现时间间隔的分布不能被理论分布拟合.
1.3 短期记忆性
概率分布并不能完整地描述重现时间间隔序列的所有统计性质,一个序列的记忆性是另一个独立于其概率分布的重要的统计性质.若某个变量的序列具有记忆效应,则该序列中后面的变量值和前面的变量值有一定的相关性.实证研究已经发现金融市场的重现时间间隔具有时间记忆效应[10-13],即处在后面的重现时间间隔和前面的实际间隔有一定关系.
根据记忆时间的长短,记忆性分为短期记忆性和长期记忆性,分别对应于物理学中的短程关联和长程关联.短期记忆性是指,序列中某个时刻的变量值和前面离它不远的变量值有一定的相关性.观测重现时间间隔的短期记忆性,可通过计算重现时间间隔的条件概率分布P(τ|τ0),即紧接着时间间隔τ0之后出现时间间隔τ的概率.在大波动的重现时间间隔研究中,该变量和市场风险估计密切相关,表示前一个大波动事件距离当前大波动事件的时间间隔为τ0,下一个大波动事件在时间τ之后发生的概率.
1.4 长期记忆性
重现时间间隔不仅具有短时记忆性,还具有长期记忆性,即某个时刻的重现时间间隔和较长时间前的重现时间间隔具有相关性.DFA(detrend fluctuation analysis)方法是研究时间序列长期记忆性的一种常用方法,DFA方法被广泛应用于分形和多重分形的研究[28-29],其二阶的降趋波动函数(detrended fluctuation function)可用来测量时间序列的记忆性[30].相比较于其它方法,DFA方法对于不稳定的时间序列也适用,可以避免因时间序列不稳定而引起的伪相关性的干扰.
假设存在一个时间序列Ni(i=1,2,…,N),将该时间序列进行如下累加处理

其中

对于一个给定的时间窗口长度s,计算其二阶降趋波动函数(detrended fluctuation function)
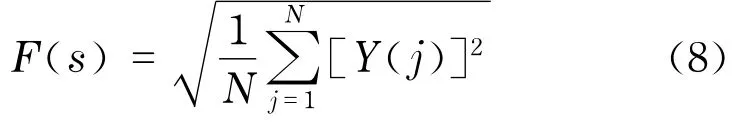
对不同的时间窗口长度s都重复上述运算,就可以得到不同s值下的降趋波动函数F(s).F(s)和s存在标度关系(scaling relation)

参数α称为Hurst指数,该指数取值表征序列的记忆特性:若α=0.5,则序列没有相关性;若α>0.5,则序列存在正相关性;若α<0.5,则序列存在负相关性[33].
2 实证分析
2.1 波动率(vo1ati1ity)
首先采用30只在深交所和上交所上市交易的股票的1分钟数据,数据的时间跨度为2004年1月到2006年6月,分析中国股市价格波动率的重现时间间隔[23,31].波动率R(t)定义为价格对数收益的绝对值
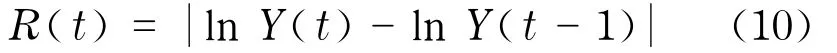
式中Y(t)为第t分钟股票的价格.
波动率具有日内效应(intraday pattern),即接近开盘和收盘的时候,波动率较大.可定义日内平均波动率
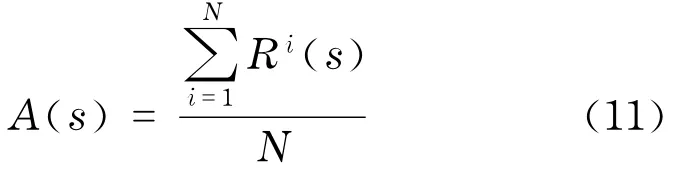
式中Ri(s)表示第i个交易日内s时刻的波动率.
如图2所示,日内平均波动率A(s)呈现“U”型形状.
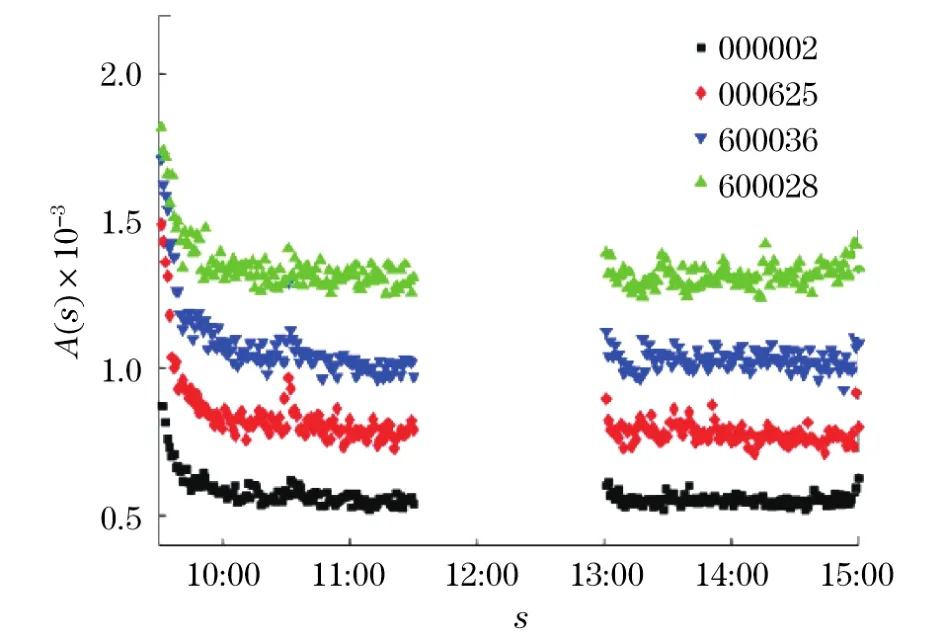
图2 上海和深圳证券交易所内个股的日内平均波动率Fig.2 Mean intraday volatility of four representative stocks in Shanghai and Shenzhen Stock Exchanges
波动率的日内效应对波动率的重现时间间隔测量有一定影响,会引起以天为周期的周期性效应.因此,在测量波动率的重现时间间隔之前,先要消除日内效应
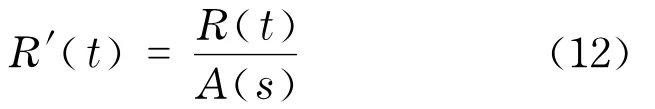
然后,再对消除日内效益的波动率做归一化处理
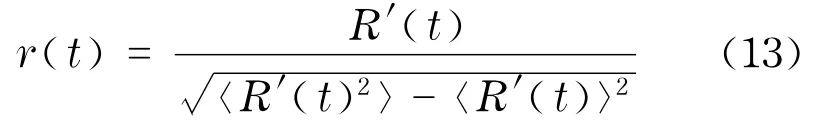
采用1.1节的定义,计算归一化波动率在不同阈值q下的重现时间间隔τ,观测重现时间间隔τ的概率分布.如图3所示的是两只股票(000839和000625)的重现时间间隔的累积概率分布,可以看出000839这只股票不同阈值下的分布不能很好地重合在一条线上,而000625这只股票不同阈值下的分布能较好地重合在一条线上,具有标度行为
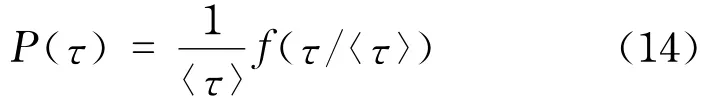
式中<τ>为平均重现时间间隔.
在30只个股中,找到12只个股具有较好的标度行为,假设其分布满足拉伸指数分布
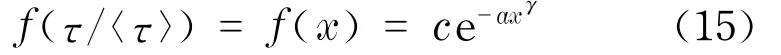
将q=2和q=5时标度后的重现时间间隔τ/<τ>合并,用最小二乘方法拟合两者共同的拉伸指数分布,然后采用1.2节介绍的拟合优度检验方法验证以上假设,即q=2和q=5时,τ/<τ>的分布都符合它们共同的拉伸指数拟合分布.根据表1的结果,同时采用KS和KSW统计量有6只股票在5%的显著性水平下通过检验,即它们的重现时间间隔分布具有标度行为,且分布服从拉伸指数分布.关于重现时间间隔分布标度行为的验证,还可以采用重现时间间隔的m-阶矩测量方法[21].
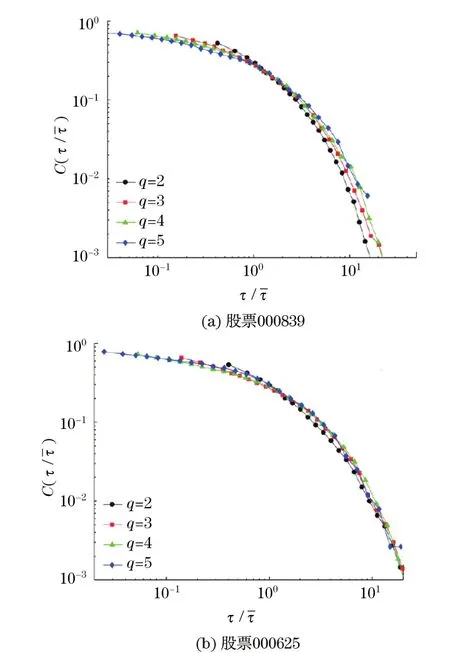
图3 个股000839和000625波动率重现时间间隔的累积概率分布Fig.3 Complementary cumulative distribution of the volatility return intervals for stock 000839 and stock 000625
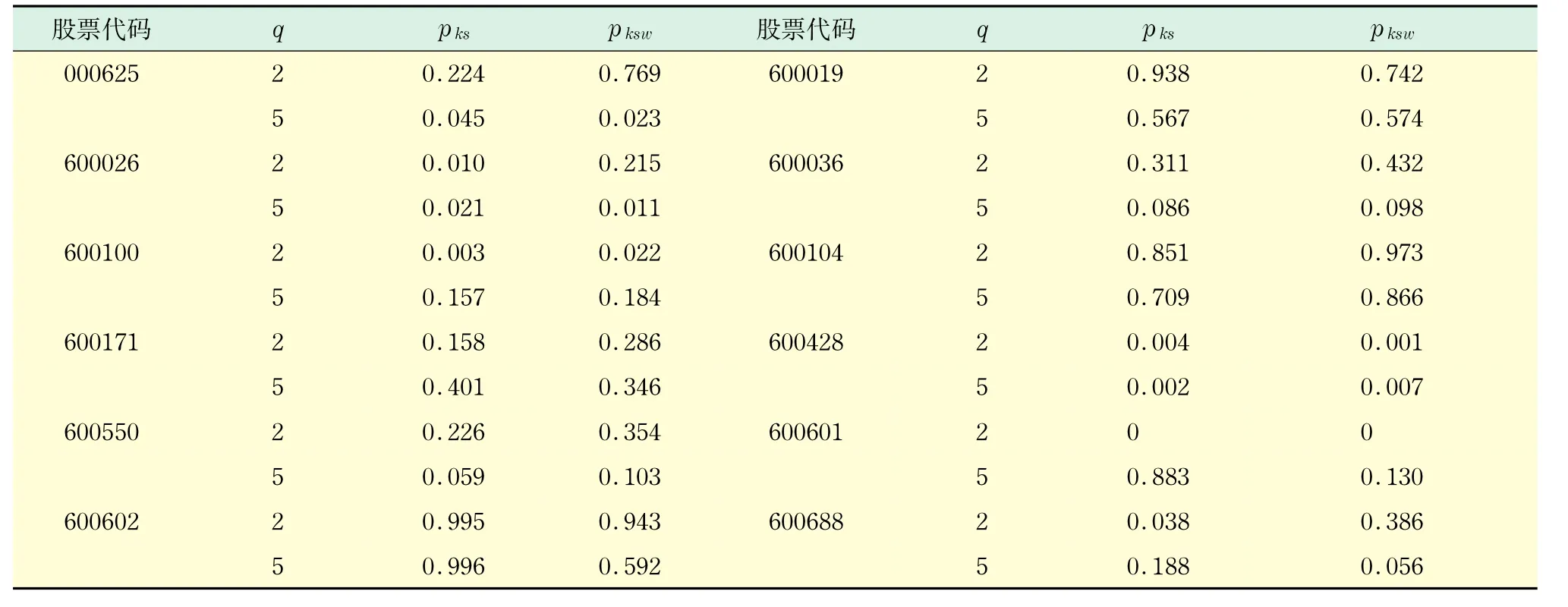
表1 上海和深圳证券交易所内个股的KS拟合优度检验结果Tab.1 KS-goodness-of-fit test for the individual stocks in Shanghai and Shenzhen Stock Exchanges
另外,我们还发现波动率的重现时间间隔同时具有短期记忆性和长期记忆性.通过计算条件概率分布,可观测重现时间间隔的短期记忆性.假设一只股票的回复事件间隔序列有N个记录,先将各个记录按升序排列后,平均分割成4个子集,记为Q1, Q2,Q3,Q4,最小的1/4回复时间间隔记录在Q1中,而最大的1/4回复时间间隔记录在Q4中,分别计算τ0落在Q1和Q4这两个子集里的条件概率密度函数Pq(τ|τ0).
图4给出了股票000002以τ/<τ>为自变量,条件概率密度函数Pq(τ|τ0)为因变量的图像,空心的符号表示τ0来自子集Q4,即重现时间间隔最大的子集,实心的符号表示τ0来自子集Q1,即重现时间间隔最小的子集.可以观测到,对于较大的τ/ <τ>,τ0∈Q4的Pq(τ|τ0)要比τ0∈Q1的Pq(τ|τ0)大,而对于较小的τ/<τ>,τ0∈Q4的Pq(τ|τ0)要比τ0∈Q1的Pq(τ|τ0)小,在其它股票中也观测到类似的现象.说明较小的重现时间间隔τ0之后更趋向于出现一个小的重现时间间隔,而大的重现时间间隔τ0之后更趋向于出现一个大的重现时间间隔,该结果表明的波动率的回复时间间隔具有短期记忆性.
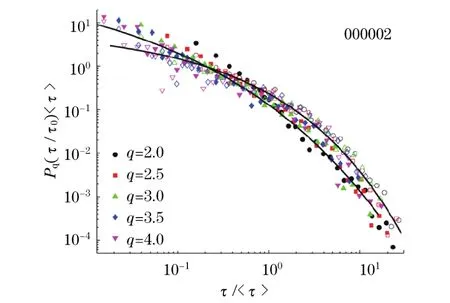
图4 股票000002的波动率重现时间间隔的条件概率密度函数Fig.4 Conditional probability distribution function of the scaled return intervals for a representative stock 000002
我们还采用1.4节介绍的DFA方法,来研究波动率的重现时间间隔的长期记忆性.图5给出了30只股票的Hurst指数,圆圈表示的是波动率的重现时间间隔的Hurst指数,所有股票的Hurst指数都远远大于0.5,说明波动率的重现时间间隔序列具有长期记忆性.方块表示的是将波动率序列随机打乱后,产生的重现时间间隔序列的Hurst指数,大都落到了H=0.5这条线附近,长期记忆性被去除掉了.该结果表明重现时间间隔序列的长期记忆性可能来源于原始波动率序列的记忆效应.
2.2 已实现波动率(rea1ized vo1ati1ity)
上文介绍了波动率的重现时间间隔,采用对数收益的绝对值定义波动率,是金融物理学中比较常见的定义方法.但波动率的定义多种多样,研究不同定义下的波动率重现时间间隔的普适性和非普适性特征具有一定意义.在主流经济学研究中,通常用一段时间内的价格方差来度量波动率,例如Anderson 等[32]采用日内价格对数收益的平方和定义日度的已实现波动率.借鉴该定义,将t到t-1时间内所有交易的对数收益率的绝对值之和定义为已实现波动率
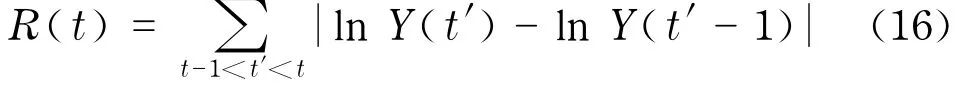
式中Y(t′)为t到t-1时间内t′时刻发生的交易的成交价.
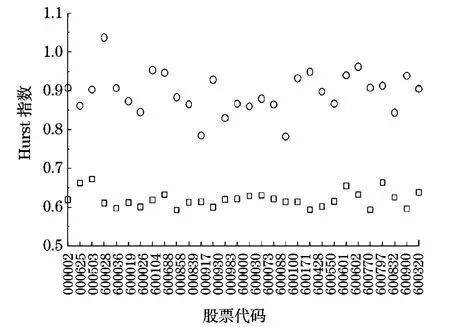
图5 上海和深圳证券交易所内个股的波动率重现时间间隔的Hurst指数Fig.5 Hurst exponents for large scales(circles)and small scales(squares)for the stocks in Shanghai and Shenzhen Stock Exchanges
采用在上海证券交易所上市的22只股票2004 年1月到2006年6月的日内超高频数据,该数据包含了这22只股票所有分笔交易的信息,在此基础上构造了1分钟的已实现波动率,即每分钟内所有交易的对数收益率的绝对值之和.图6比较了采用前一章定义的波动率和已实现波动率的重现时间间隔分布,发现不同阈值q下已实现波动率的重现时间间隔分布重合性更好,说明已实现波动率的重现时间间隔分布具有更好的标度行为.进一步研究表明,部分股票的已实现波动率的重现时间间隔分布满足拉伸指数分布,能通过KS拟合优度检验,并且已实现波动率的重现时间间隔也具有短期和长期记忆性[33].
2.3 收益率(return)
股票的收益率直接关系到价格的涨跌情况,因此研究收益率的重现时间间隔,对股票市场的风险估计和管理研究具有比较重要的意义.采用在上交所和深交所上市的20只个股2000年1月至2009 年5月、上证综指和深证综指2003年1月至2009 年4月的1分钟数据,研究中国股市收益率的重现时间间隔[24].收益率R(t)定义为价格的对数收益, Y(t)为第t分钟股票或指数的价格,则采用1.1节中的重现时间间隔定义,计算收益率大于阈值q>0和小于阈值q<0的重现时间间隔.图7给出了上证综指和深证综指在不同阈值下的重现时间间隔分布,可以看出阈值为负和阈值为正的分布是重合的,因此分布具有式(14)的标度率行为.
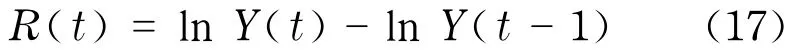
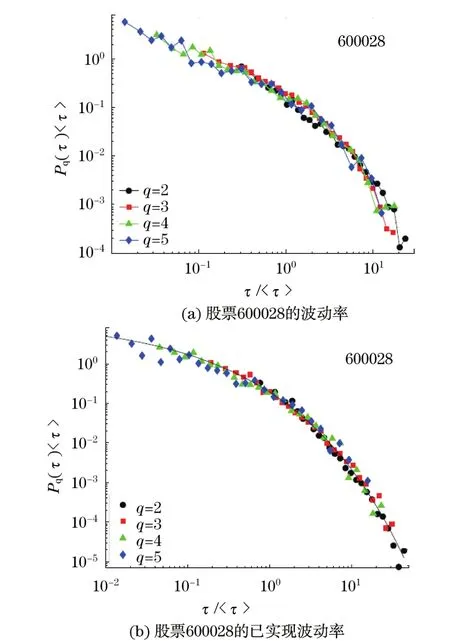
图6 股票600028的波动率(左)和已实现波动率(右)的重现时间间隔的概率分布Fig.6 Probability distributions of the return intervals of volatilities and realized volatilities for stock 600028
和波动率的重现时间间隔分布不同,收益率的重现时间间隔尾分布呈幂律分布形态.假设收益率的重现时间间隔的尾分布满足幂律分布
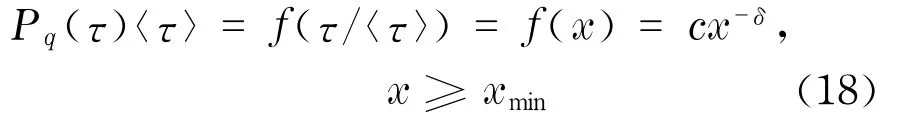
我们将不同阈值下q的标度重现时间间隔τ/<τ>合并,用Newman[27]的极大似然估计方法估计它们共同的拟合分布参数,然后用KS拟合优度检验方法检验不同阈值的尾分布是否和它们共同的拟合分布一致.表2(见下页)罗列了对上证综指、深证综指和20只个股的p- value值.在1%的显著水平下,若采用KS统计量,上证综指通过拟合优度检验,若同时采用KS和KSW统计量,上证综指和16只个股通过拟合优度检验,说明对于大多数股票,收益率重现时间间隔的尾分布具有标度率,且分布服从幂律分布.
研究还发现阈值q和重现时间间隔的均值<τ>存在幂律关系
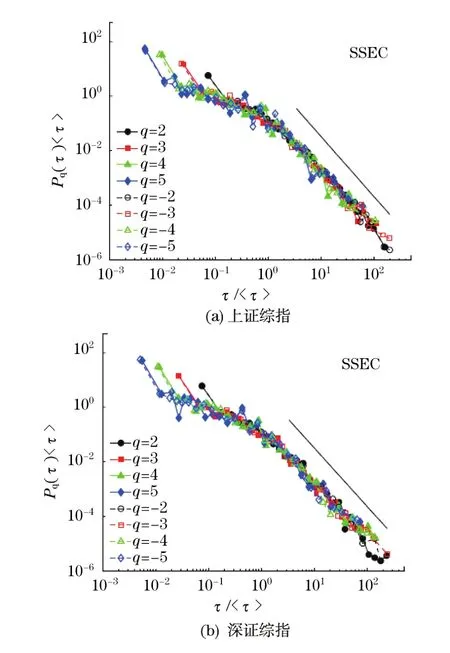
图7 上证综指(SSEC)和深证综指(SZCI)收益率的重现时间间隔分布Fig.7 Probability distributions of the recurrence intervals of returns for SSEC and SZCI
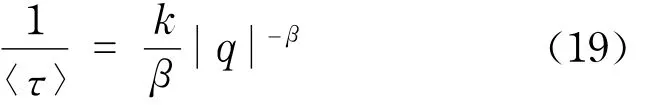
上证综指和深证综指收益率的重现时间间隔均值和阈值关系如图8(见下页)所示,该结果和同一时期发表在《美国科学院院报》上的一篇文章的结果一致[34].并结合条件重现时间间隔<τ|τ0>的结果,提出了一个风险估计模型
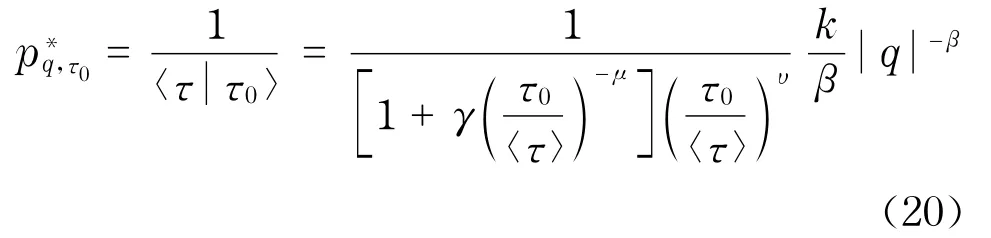
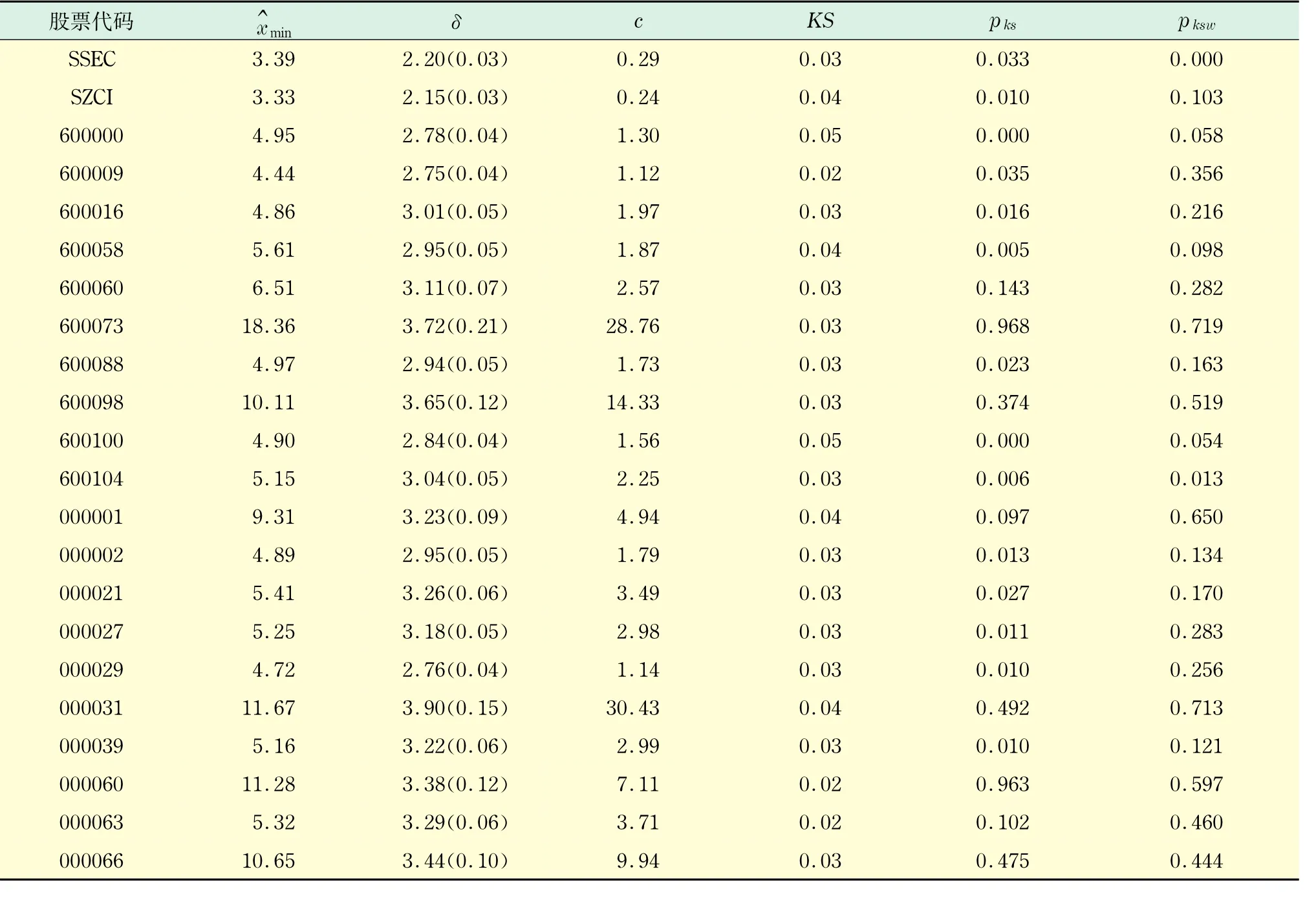
表2 上证综指、深证综指和20只个股的KS拟合优度检验结果Tab.2 KS-goodness-of-fit test for the individual stocks in Shanghai and Shenzhen Stock Exchanges
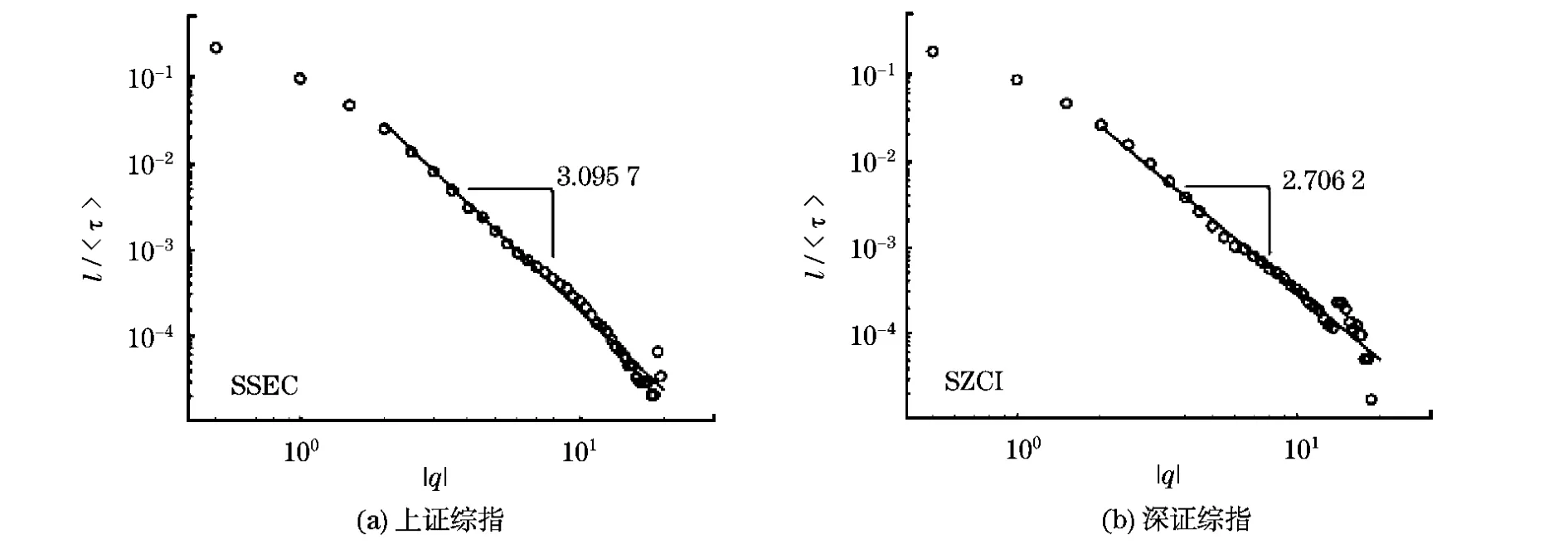
图8 上证综指和深证综指收益率的重现时间间隔均值和阈值关系Fig.8 Reciprocal of mean recurrence interval 1/<τ>as a function of absolute threshold |q|for SSEC and SZCI
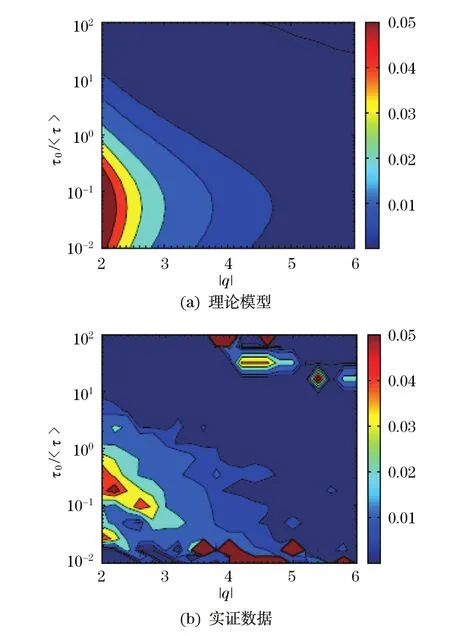
图9 上证综指理论模型和实证数据的条件损失概率的等高图Fig.9 Contour maps of theoretical loss probability and empirical loss probability
2.4 交易量(trading vo1ume)
最近,重现时间间隔的研究拓展到交易量的研究中[25-26],并从时间间隔角度考察了大波动和大交易量的关系[25].采用在上交所和深交所上市的20只个股2000年1月至2009年5月、上证综指和深证综指2003年1月至2009年4月的1分钟数据,分析中国股市交易量的重现时间间隔[25].研究发现,交易量的重现时间间隔尾分布也服从式(18)的幂律分布,如图10所示,并采用KS拟合优度检验和Cv M拟合优度检验验证了尾分布的幂律形式.相关研究还表明,交易量的重现时间间隔序列也具有短期记忆性和长期记忆性.
我们还进一步考察了大交易量时间间隔和大波动时间间隔的同步性,用阈值q定义交易量的重现时间间隔,Q定义波动率的重现时间间隔.图11(见下页)给出的是大波动和大交易量具有相同时间间隔周期的概率,相同波动率阈值Q下交易量阈值q越大,时间间隔同周期的概率越大,说明大波动通常伴随大交易量同时出现.
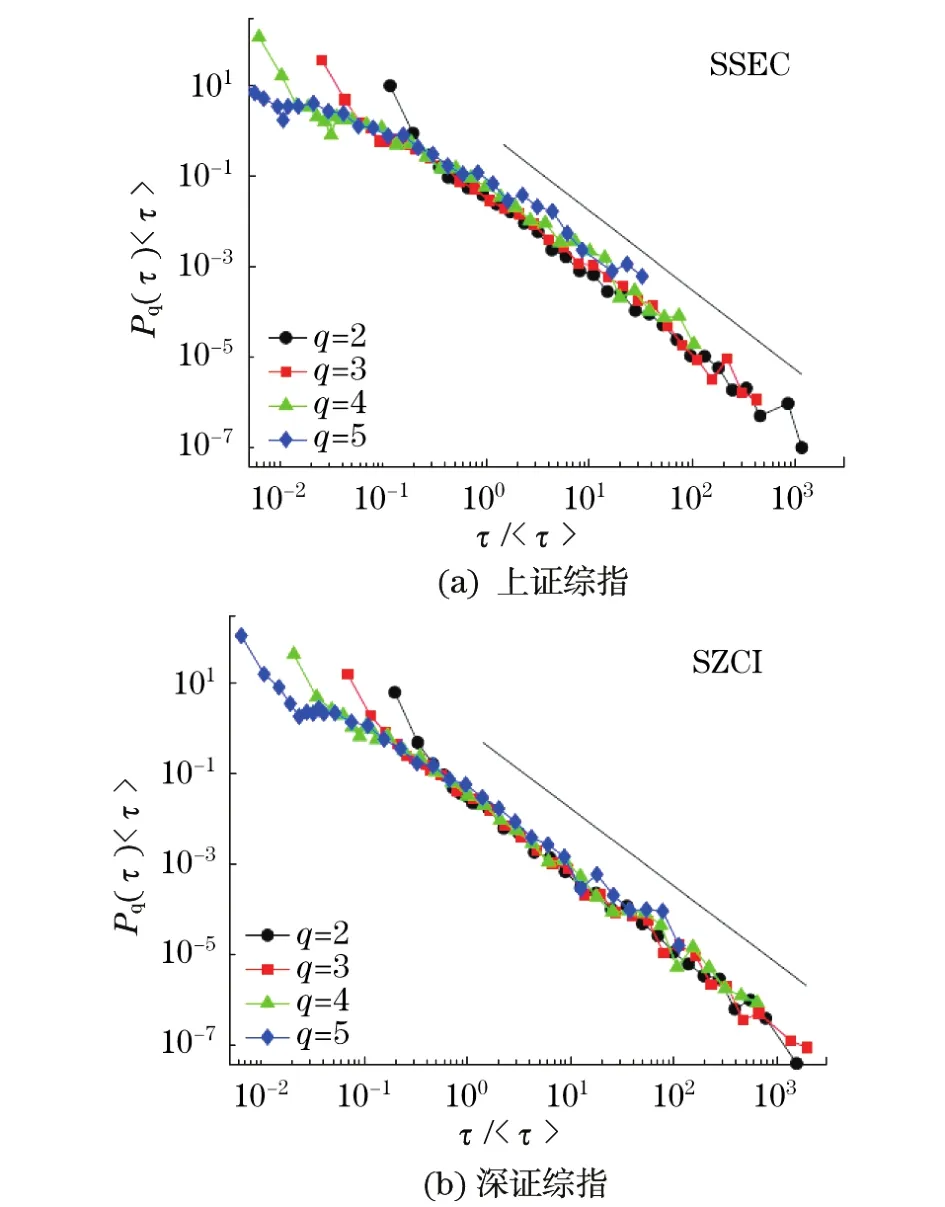
图10 上证综指(SSEC)和深证综指(SZCI)交易量的重现时间间隔分布Fig.10 Probability distributions of the recurrence intervals of trading volumes for SSEC and SZCI
3 微观模型模拟结果
本节将采用委托驱动市场模型[35],模拟产生股票的价格序列,并运用该价格序列分析收益率的重现时间间隔.首先简单描述一下模型的定义和几个相关参数.委托驱动市场模型是基于交易所内连续委托竞价的交易模式提出的,其构型和实际市场非常接近:市场内有若干个经纪人(agent),每个经纪人根据各自的策略递交委托订单,每个订单包含委托方向(买或者卖)、委托价格和委托量的信息,所有经纪人的委托指令被存储在指令簿(order book)内,系统会根据指令簿内的委托订单信息撮合成交,成交价格即当前股票的价格.
该模型的委托订单包含三方面的信息,首先我们将经纪人的委托量简化为一个基本单位,即每人每次可以买卖一股股票,经纪人委托订单的另外两方面信息由参数Hs和Hx决定,Hs用来度量委托方向的记忆性,Hx用来度量委托价格与指令簿最优价格的相对价格的记忆性.通过调节参数Hs和Hx,可以观测模拟价格的动力学演化过程,研究不同参数域下收益率的重现时间间隔.
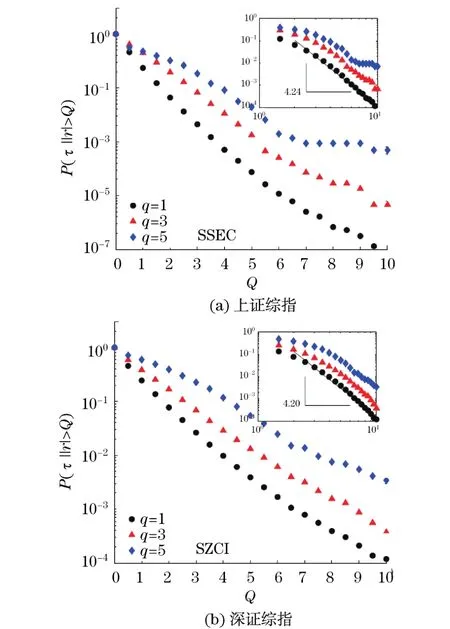
图11 上证综指(SSEC)和深证综指(SZCI)大波动和大交易量的时间间隔关系Fig.11 Probability of volume intervals conditioned on large volatilities|r|>Q for SSEC and SZCI
图12给出了Hx=0.75和Hs=0.5时,模拟价格的收益率的重现时间间隔分布,分布的中间部分呈现出幂律分布的形态,类似于实证数据的幂律分布.分布的尾巴部分衰落得比较快,这可能是由于体系的有限尺度效应引起的.结合上述的两种分布形态,假设模型收益率的重现时间间隔分布满足以下分布
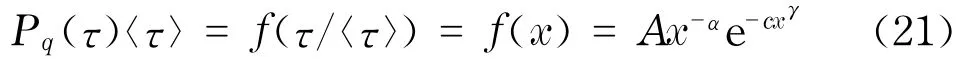
采用Newman[27]的极大似然估计方法估计分布参数,发现幂指数α和参数Hs没有显著的关系,和参数Hx呈线性关系,如图13所示.
进一步假设幂指数α与参数Hs和Hx存在线性关系
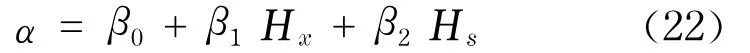
采用最小二乘法得到的线性回归系数为β1= 0.665,β2=-0.017.参数Hx前的系数在1%的显著水平下显著不为零,Hs前的系数在1%的显著水平下不显著不为零,这和图13的结果一致.分布的幂指数α与参数Hs线性相关,而参数Hs决定了收益率(大于零的单侧收益率)原始序列的记忆效应,进一步证实了收益率的重现时间间隔分布和原始序列的记忆性相关.
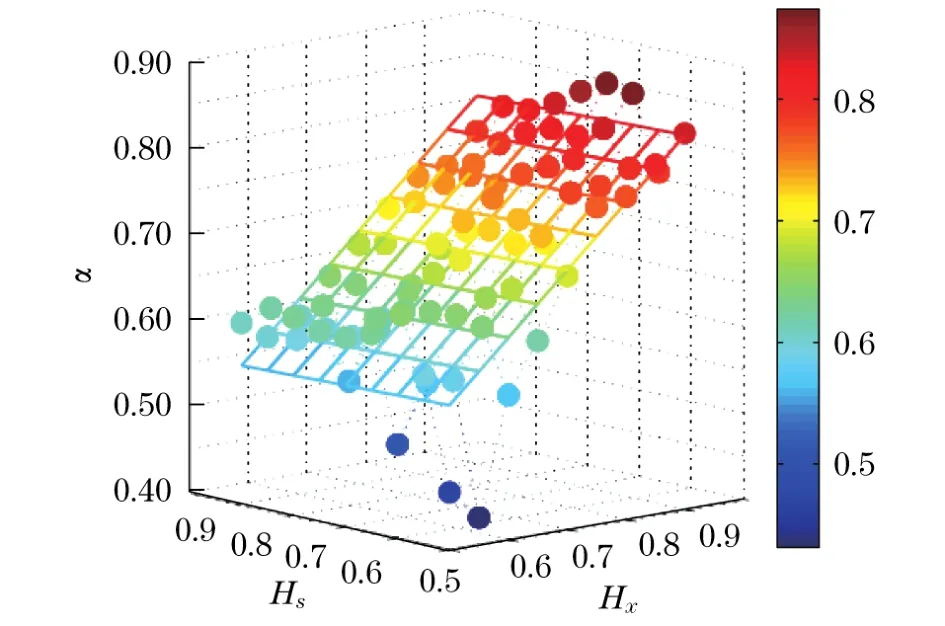
图13 委托驱动市场模型的重现时间间隔分布的α指数与Hs和Hx参数的关系Fig.13 Scaling exponentαof the recurrence intervals generated from an order-driven model as a function of the variables Hsand Hx
4 结 论
本文采用中国股市的高频数据,对中国金融市场大波动极端事件的重现时间间隔进行研究.首先介绍了重现时间间隔的概念和基本理论,并介绍了考察重现时间间隔分布和记忆效应的几种分布检验和关联测度方法,例如KS和KSW拟合优度检验、条件概率分布和DFA方法.本文对波动率、已实现波动率、收益率和交易量的重现时间间隔进行了实证分析,揭示了重现时间间隔分布的非高斯特征,采用拟合优度检验方法确立了收益率和交易量重现时间间隔的幂律尾分布形式,进一步验证了重现时间间隔的短期和长期记忆特性,从重现时间间隔分析的角度揭示大波动和大交易量之间的协同关系,并基于收益率重现时间间隔分析,提出了VaR风险估计模型.本文还运用委托驱动的微观模型,研究大波动极端事件重现时间间隔的动力学机理,发现重现时间间隔的分布和价格波动序列的记忆性相关,证实记忆效应在大波动极端事件研究中的重要性.
[1] BOUCHAUD J P.Economics needs a scientific revolution[J].Nature,2008,455:1181.
[2] LUX T,WESTERHOFF F.Economics crisis[J].Nature Physics,2009,5(1):2-3.
[3] 张维,张永杰,熊熊.计算实验金融研究[M].北京:科学出版社,2010.
[4] 盛昭瀚,张军,杜建国.社会科学计算实验理论与应用[M].上海:上海三联出版社,2009.
[5] 盛昭瀚,张维.管理科学研究中的计算实验方法[J].管理科学学报,2011,14(5):1-10.
[6] 周炜星.金融物理学导论[M].上海:上海财经大学出版社,2007.
[7] BUNDE A,EICHNER J F,HAVLIN S,et al.Return intervals of rare events in records with long-term persistence[J].Physica A,2004,342(1/2):308-314.
[8] BUNDE A,EICHNERJ F,KANTELHARDT JW,et al. Long-term memory:A natural mechanism for the clustering of extreme events and anomalous residual times in climate records[J].Physical Review Letters,2005, 94(4):048701.
[9] LIVINA V N,HAVLIN S,BUNDE A.Memory in the occurrence of earthquakes[J].Physical Review Letters,2005,95(20):208501.
[10] YAMASAKI K,MUCHNIK L,HAVLIN S,et al.Scaling and memory in volatility recurrence interval in financial markets[J].Proceedings of the National Academy of Sciences of the United States of America,2005,102 (26):9424-9428.
[11] WANG F Z,YAMASAKI K,HAVLIN S,et al.Scaling and memory of intraday volatility recurrence intervals in stock markets[J].Physical Review E,2006,73 (2):026117.
[12] OLLA P.Return times for stochastic processes with power-law scaling[J].Physical Review E,2007,76 (1):011122.
[13] SANTHANAM M S,KANTZ H,Return interval distribution of extreme events and long term memory[J]. Physical Review E,2008,78(5):051113.
[14] EICHNER J F,KANTELHARDT JW,BUNDEA,et al. Extreme value statistics in records with long-term persistence[J].Physical Review E,2006,73(1): 016130.
[15] EICHNER J F,KANTELHARDT JW,BUNDEA,et al. Statistics of recurrence intervals in long-term correlated records[J].Physical Review E,2007,75(1): 011128.
[16] JUNG W S,WANG F Z,HAVLIN S,et al.Volatility recurrence intervals analysis of the Japanese market[J]. European Physical Journal B,2008,62(1):113-119.
[17] WANG F Z,YAMASAKI K,HAVLINS,et al.Indication of multiscaling in the volatility recurrence intervals of stock markets[J].Physical Review E,2008,77 (1):016109.
[18] LEE J W,LEE K E,RIKVOLD P A.Waiting-time distribution for Korean stock-market index KOSPI[J]. Journal of the Korean Physical Society,2006,48(92): 123-126.
[19] BOGACHEV M I,BUNDE A.Memory effects in the statistics of interoccurrence times between large returns in financial records[J].Physical Review E, 2008,78(3):036114.
[20] ALYMANN E G,KANTZ H.Recurrence time analysis, long-term correlations,and extreme events[J].Physical Review E,2005,71(5):056106.
[21] BOGACHEV M I,EICHNER J F,BUNDE A.Effect of nonlinear correlations on the statistics of return intervals in multifractal data sets[J].Physical Review Letters,2007,99(24):240601.
[22] QIU T,GUO L,CHEN G.Scaling and memory effect in volatility recurrence interval of the Chinese stock market[J].Physica A,2008,387(27):6812-6818.
[23] REN F,ZHOU W X.Multiscaling behavior in the volatility recurrence intervals of Chinese indices[J].Europhysics Letters,2008,84(6):68001.
[24] REN F,ZHOU W X.Recurrence interval analysis of high-frequency financial returns and its application to risk estimation[J].New Journal of Physics,2010,12 (7):075030.
[25] REN F,ZHOU W X.Recurrence interval analysis of trading volumes[J].Physical Review E,2010,81 (6):066107.
[26] LI W,WANGFZ,HAVLINS,et al.Financial factor influence on scaling and memory of trading volume in stock market[J].Physical Review E,2011.(in press)[27] CLAUSET A,SHALIZI C R,NEWMAN M E J.Powerlaw distributions in empirical data[J].SIAM Review, 2009,51(4):661-703.
[28] 周炜星.上证指数高频数据的多重分形错觉[J].管理科学学报,2010,13(3):81-86.
[29] MANDELBROT B B.Long-run interdependence in price records and other economic time series[J]. Econometrica,1970,38(4):122-123.
[30] HU K,IVANOV PC,CHEN Z,et al.Effect of trends on detrended fluctuation analysis[J].Physical Review E, 2001,64(1):011114.
[31] REN F,GUO L,ZHOU W X.Statistical properties of volatility return intervals of Chinese stocks[J].Physica A,2009,388(6):881-890.
[31] ANDERSEN T G,BOLLERSLEV T,DIEBOLD F X,et al.The distribution of realized stock return volatility [J].Journal of Financial Economics,2001,61(1):43-76.
[33] REN F,GU G F,ZHOU W X.Scaling and memory in the return intervals of realized volatility[J].Physica A,2009,388(22):4787-4796.
[34] PODOBNIK B,HORVATIC D,PETERSEN A M,et al. Cross-correlations between volume change and price change[J].Proceeding of the National Academy of Sciences of the United States of America,2009,106(52): 22079-22084.
[35] GU G F,ZHOU W X.Emergence of long memory in stock volatilities from a modified Mike-Farmer model [J].Europhysics Letters,2009,86(4):48002-48007.
Recurrence interval analysis of complex financial systems
RENΝei, GUGao-feng, JIANGZhi-qiang, ZHOUWei-xing
(School of Busimess,East Chima Umiversity of Sciemce amd Techmology,Shamghai 200237,Chima)
This paper uses the methods of complex science,and studies the statistical properties of probability distribution and memory effect of the recurrence intervals,defined as the intervals between extreme events in financial markets.Relatively accurate analysis is performed by using various goodness-of-fit tests and memory effect detecting methods.The application of the recurrence interval analysis in financial complex systems is systematically introduced,including the empirical studies of recurrence intervals of volatilities,realized volatilities,returns and trading volumes. Based upon this study,we perform a primarily risk estimation for the stock market.Furthermore, an order driven model is introduced.The dynamics of the recurrence intervals between extreme events is studied by mimicking the order submission process of the investors in stock markets.This work may provide a theoretical foundation for the risk estimation and avoiding of extreme events in the Chinese stock market.
ecomophysics;extreme evemts;recurremce imterval amalysis;fimamcial risk
F 830.91文献标示码:A
1007-6735(2011)05-0433-11
2011-09-16
任 飞(1980-),女,副教授.研究方向:金融复杂系统、金融工程、金融风险控制与监管. E-mail:fren@ecust.edu.cn
