平面绳索牵引并联机器人静态刚度

王克义，孟浩，张立勋，郭培培

(1.哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨 150001;2.哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001)

绳索牵引并联机器人作为一种柔性冗余驱动并联机构，相对传统刚性并联机构而言，具有惯性小、运动空间大和运动速度快等优点，但绳索只能承受拉力是该类机构的特点，由于绳索本身具有一定的弹性［1-2］，所以动平台的静态刚度相对刚性并联机构有所降低，影响系统的定位精度［3］.分析影响绳索牵引并联机器人动平台静态刚度因素以及寻找提高静态刚度的有效措施具有重要的理论意义和现实意义.利用非线性方程表征绳索牵引并联机器人的绳索刚度，分析绳索拉力对刚度的影响情况并进行了仿真，研究了绳索弹性对动态响应的影响［4］.通过分析单根绳索的等效弹簧模型，推导了冗余驱动绳牵引并联机器人的刚度表达，进行了刚度控制分析［5］;也有通过建立系统的静力学平衡方程，根据刚度定义概念，得出动平台静态刚度主要由绳索刚度决定和绳索几何布置，绳索的预紧力对静态刚度影响可以忽略不计［6-7］.基于所建立的系统运动学方程和力平衡方程，通过微分变换方法，得出绳索牵引并联机器人动平台静态刚度的影响由绳索刚度和绳索拉力决定，且两者之间影响处于独立关系［8］.根据增大绳索拉力可以增强系统刚度，建立了基于刚度的运动控制模型，并进行了仿真分析［9-11］.上述仿真研究均通过所建立的数学模型进行的数值仿真，本文以平面1R2T完全约束定位机构的绳索牵引并联机器人为对象，分析影响动平台静态刚度的因素，并用ANSYS软件建立机器人系统的有限元模型，仿真施加外力后的动平台变形.该研究对绳索牵引系统的定位精度和运动控制研究具有指导性意义.

1 机器人机构

平面绳索牵引并联机器人系统如图1所示，绳索的一端(Pi，i=1，2，3，4)通过铰链与动平台相连，另一端绕过框架上分布的过轮(Bi)与电动机驱动的绞盘相连，电动机带动绞盘实现绳索的控制，以此动态地调节动平台的位姿，约束机构用于限制动平台的运动输出形式，位置检测用于对动平台的直接测量，其与电动机编码器测得的数值相对比，可以知道绳索刚度对位姿控制精度的影响，串联在绳索回路中的力传感器用于绳索拉力的监控.

图1 平面绳索牵引机器人Fig.1 Plane wire-driven parallel robot

建立世界坐标系oxy和局部坐标系pxpyp，局部坐标系固联在动平台中心，如图2所示，其中 Bi(i=1，2，3，4)为绳索与过轮的连接点，Pi为绳索与动平台的连接点，该点与局部坐标系中心的矢量为ri=PPi，绳 索 矢 量 为 Li=PiBi，绳 索 长 度 为li=‖Li‖，绳索单位矢量为 ui=Li/li，ti为第 i根绳所受的拉力.

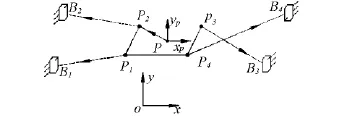
图2 平面绳索牵引机器人模型Fig.2 Model of plane wire-driven parallel robot

2 静态刚度分析

已知动平台控制所处位姿，由逆运动学可求解绳索长度.令动平台中心位姿为X= [Px，Py，θ]T，可以求得Pi的位置:

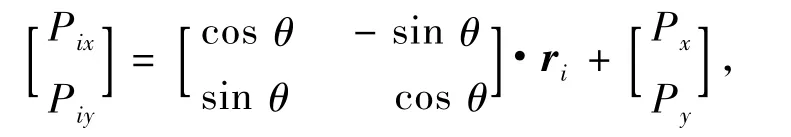
从而计算出绳索的长度:

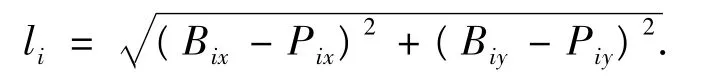
当已知3根绳索长度时，考虑动平台所处工作空间是由Bi构成的凸集所确定，便可确定动平台所处位姿.由于绳索不能承受压力，为保证系统力的可控性［12］，需4根绳索牵引，这使得机器人在运动学上体现出不相容性，故4根牵引绳索之间需满足位置协调方程，同时在位置协调方程的影响下也避免了机器人正运动学的多解.

根据平衡条件，建立系统力螺旋平衡方程:

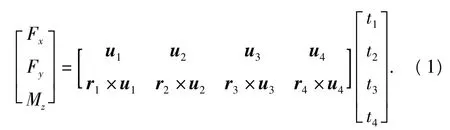
简化为

式中:J为力映射矩阵.

考虑到力映射矩阵与速度映射矩阵是互为转置，故:

式中:L为绳索长度矩阵，L= [llll]T.1234

根据刚度定义，并依据微分变换原理可得绳索牵引机器人的静态刚度为［10］

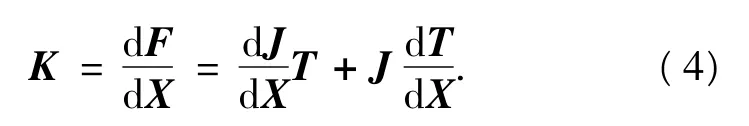
式中:K= [KxKyKθ]T代表动平台3自由度的运动刚度.考虑到dT=d[ t1t2t3t4]T，又由于绳索拉力的微分dti与绳索刚度ki和绳索长度的微分dli之间的关系为将式(5)代入式(4)的中，并考虑式(3)，则有

这说明绳索刚度和绳索布置方式影响特定位姿处动平台的静态刚度.而绳索刚度本身还取决于绳索未受拉力时的长度li0，即动平台处于固定位姿时，绳索变形后的长度li是一定的，则绳索拉力将影响绳索长度li0，从而影响了绳索轴向刚度［12］.由变形条件可列方程:

式中:E为绳索弹性模量，A为绳索横截面积，Δi为绳索变形量.从式(7)可以看出，增大绳索拉力，绳索表现出的刚度将增大，该增大值与绳索的弹性模量、横截面积和长度有关，可见绳索拉力增大在部分中起到间接地增大动平台静态刚度的作用.有关式(4)中是代表绳索拉力对动平台静态刚度的直接影响，文献［8］利用虚功原理对该部分进行了分析.本文将针对不同绳索拉力条件下动平台受外力作用前后的运动量进行有限元分析，寻找绳索拉力对牵引系统动平台静态刚度的影响规律.通过对式(2)求解可得绳索拉力:

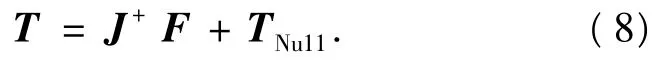
式中:J+=JT(JJT)-1为J的广义逆，J+F为方程最小范数解，TNu11=λNu11(J)为绳索拉力零空间解向量，λ为正常数，Nu11(J)为J的零空间基向量，通过选取不同λ的可以确定不同的绳索拉力.

3 有限元仿真

参考图 2，设计过轮中心 Bi(i=1，2，3，4)在世界坐标系中的坐标为(单位均为m)

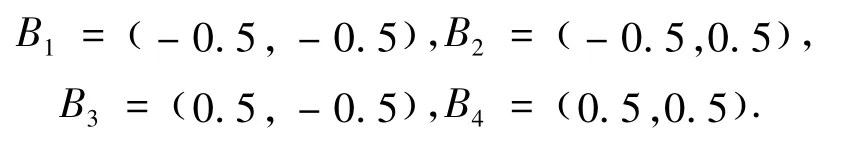
动平台的结构尺寸为0.3×0.2，对应的连接点Pi(i=1，2，3，4)在局部坐标系中的坐标为

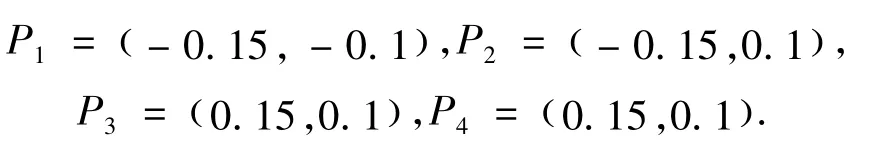
通过ANSYS软件建立平面绳索牵引并联机器人模型，考虑到牵引绳索的受力特性，即仅能承受拉力不能承受压力，故选择有限元单元LINK10作为绳索划分单元，它独特的双线性刚度矩阵特性使其成为一个轴向仅受拉或仅受压的杆单元(该仿真设置为受拉选项，仅受拉)，使用仅受拉选项时，如果单元受压，刚度就消失，以此来模拟绳索的松弛;此外在该单元的实常数中可以设置绳索的初始应变，以此实现仿真中要针对不同的绳索初始拉力条件，所以每根绳索的初始应变根据不同的条件分别进行设置.绳索牵引系统中牵引绳索的连接点处可以实现绕任意方向转动，即可等效为球铰，而在平面绳索牵引机器人中绳索在过轮和动平台的连接点，可以认为是绕垂直轴的铰链.在ANSYS软件中，选择有限单元COMBIN7模拟铰链，该单元是一个三维6自由度铰链连接单元，具有转动控制功能.

定义机器人在某一运动方向上的等效静态刚度为

式中:ΔF为作用在某一运动方向上的外力;ΔX为在该运动方向上的位移量.该等效静态刚度强调的是一个运动方向上的静态刚度，并未考虑ΔF所引起其他运动方向上的耦合运动量.本文利用等效刚度概念，针对不同机器人绳索牵引方案，分析绳索拉力对动平台静态刚度影响情况.典型完全约束定位机构的绳索布置方案如图3所示.

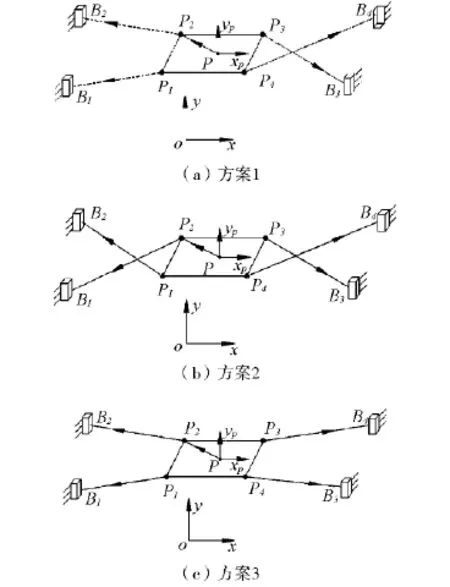
图3 机器人绳索布置方案Fig.3 The scheme of wire-driven parallel robot

对动平台处于中心位置时进行静态刚度仿真，即机器人局部坐标系与世界坐标系重合.分别设置稳态时绳索拉力最小值为 tmin=10，50，100，500，1 000，通过式(8)可以求出该姿态下每根绳索的拉力.研究动平台两平动的等效静态刚度，令ΔFx=500 N，ΔFy=500 N，分别进行仿真.当绳索拉力最小值设置较小时，从仿真云图中可以看出部分绳索已经退出牵引状态，此时绳索牵引机器人属于不完全约束定位机构.图3(a)方案仿真运动量结果如表1所示，取3位有效数字.

表1 图3(a)方案仿真结果Table 1 The simulation results of Fig.3(a)scheme

表(1)通过线性插值得到等效刚度曲线，如图4所示.从该图中可以看出，在绳索最小拉力较小(如tmin＜500 N)时，随着绳索最小拉力的增大，动平台的等效静态刚度增大，绳索拉力对系统静态刚度影响作用表现明显;而绳索最小拉力增大到一定程度(如tmin＞500 N)时，其几乎无影响作用.综上得出:绳索拉力对系统静态刚度影响是非线性.同时可以看出x轴和y轴等效刚度的变化规律并不一致，x轴数值变化范围小，最小值为254 N/mm，最大值为360 N/mm;y轴数值变化范围大，最小值为138 N/mm，最大值为505 N/mm，这与绳索牵引布置方案所关，说明该方案的y轴刚度比x轴受绳索拉力影响敏感.

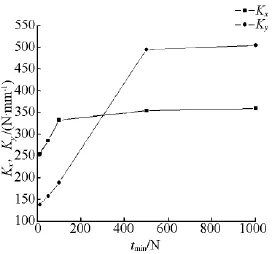
图4 方案1等效刚度曲线Fig.4 The equivalent stiffness of scheme 1

对图3(b)方案2进行等效刚度仿真，其曲线如图5所示.其绳索拉力对动平台静态刚度影响规律与图3(a)方案一致.x轴等效刚度数值变化范围小，最小值为112 N/mm，最大值为221 N/mm;y轴等效刚度数值变化范围大，最小值为331 N/mm，最大值为641 N/mm，在该方案中，y轴刚度始终比x轴大，与图3(a)方案1对比，从侧面反映出绳索牵引结构对动平台静态刚度的影响.

对图3(c)方案3进行等效刚度仿真，其曲线如图6所示.其绳索拉力对动平台静态刚度影响规律与图3(a)、(b)方案1、2一致.x轴和y轴等效刚度数值变化范围基本相同，其中 x轴的最小值为248N/mm，最大值为500N/mm;y轴的最小值为329N/mm，最大值为640N/mm，在该方案中，y轴刚度与x轴的差相对图3(b)方案2有所减小，表现出的各向刚度相对均匀，这是绳索非交叉布置的优点，但同时该布置也将降低绕z轴的运动范围.

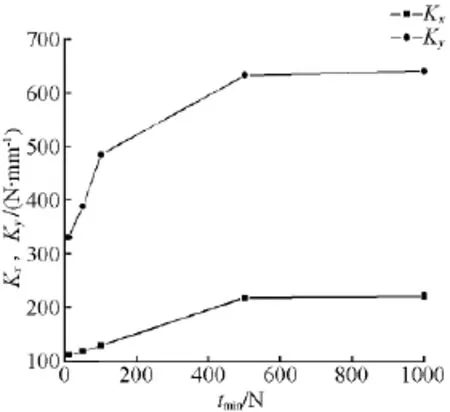
图5 方案2等效刚度曲线Fig.5 The equivalent stiffness of scheme 2

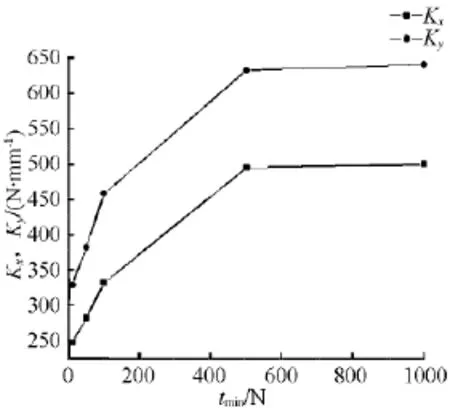
图6 方案3等效刚度曲线Fig.6 The equivalent stiffness of scheme 3

综上3种平面绳索牵引机器人静态刚度的仿真，结果说明绳索拉力对系统静态刚度影响是非线性;同时也证明了绳索布置方案同样影响动平台的静态刚度.

4 结论

1)依据所建立的平面绳索牵引机器人模型，通过对静态力螺旋平衡方程的微分变换，推导出动平台静态刚度的解析表达式，得出该刚度与绳索拉力、绳索拉伸刚度、绳索布置方案和动平台所处位姿有关.

2)根据绳索牵引特性，选择了有限单元，利用有限元软件ANSYS建立了平面绳索牵引机器人模型，定义了等效静态刚度，并进行了有限元仿真，得出在绳索最小拉力较小(如tmin＜500 N)时，随着绳索最小拉力的增大，动平台的等效静态刚度增大，绳索拉力对系统静态刚度影响作用表现明显;而绳索最小拉力增大到一定程度(如tmin＞500 N)时，其几乎无影响作用.同时证明了绳索布置方案对动平台静态刚度的影响作用.

3)该研究内容为绳索牵引系统的定位精度和运动控制研究提供指导性意义.

［1］HUANG J，HILLER M，FANG S Q.Simulation modeling of the motion control of a two degree of freedom，tendon based，parallel manipulator in operational space using MATLAB［J］.Journal of China University of Mining and Technology，2007，17(2):179-183.

［2］VARZIRI M S，NOTASH L.Kinematic calibration of a wire-actuated parallel robot［J］.Mechanism and Machine Theory，2007，42(8):960-976.

［3］王克义，郭钽，张立勋，等.绳索牵引康复机器人运动误差及仿真分析［J］.哈尔滨工程大学学报，2008，29(11):1210-1215.WANG Keyi，GUO Tan，ZHANG Lixun，et al.The simulation and movement errors analysis of wire-driven rehabilitative robots［J］.Journal of Harbin Engineering University，2008，29(11):1210-1215.

［4］KAWAMURA S，CHOE W，TANAKA S，et al.Development of an ultrahigh speed robot FALCON using wire drive system［C］//Proceedings of the 1995 IEEE International Conference on Robotics and Automation.NJ:IEEE Press，1995:215-220.

［5］SAEED B，AMIR K.Stiffness of cable-based parallel manipulators with application to stability analysis［J］.Journal of Mechanical Design，2006，128(1):303-310.

［6］BRUCKMANN T，MIKELSONS L，BRANDT T，et al.Design approaches for wire robots［C］ //Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference 2009.New York:American Society of Mechanical Engineers，2010:25-34.

［7］郑亚青.绳牵引并联机构若干关健理论问题及其在风洞支撑系统中的应用研究［D］.福建:华侨大学，2004:128-139.ZHENG Yaqing.Key theoretical issues of wire-driven parallel kinematic manipulator and applied research on wind tunnel support system［D］.Fujian:Huaqiao University，2004:128-139.

［8］隋春平，赵明扬.3自由度并联柔索驱动变刚度操作臂的刚度控制［J］.机械工程学报，2006，42(6):205-210.SUI Chunping，ZHAO Mingyang.Statics and stiffness study on a 3-DOF parallel wire driven flexible manipulator［J］.Chinese Journal of Mechanical Engineering，2006，42(6):205-210.

［9］ALALEH V，MOHAMMAD M A，HAMID D T.Integrated controller for an over-constrained cable driven parallel manipulator:KNTU CDRPM［C］//2010 IEEE International Conference on Robotics and Automation Anchorage Convention District.NJ:Institute of Electrical and Electronics Engineers Inc，2010:650-655.

［10］刘欣，仇原鹰，盛英.风洞试验绳牵引冗余并联机器人的刚度增强与运动控制［J］.航空学报，2009，30(6):1156-1164.LIU Xin，QIU Yuanying，SHENG Ying.Stiffness enhancement and motion control of a 6-DOF wire-driven parallel manipulator with redundant actuations for wind tunnels［J］.Acta Aeronautica et Astronautica Sinica，2009，30(6):1156-1164.

［11］刘攀，张立勋，王克义，等.绳索牵引康复机器人的动力学建模与控制［J］.哈尔滨工程大学学报，2009，30(7):811-815.LIU Pan，ZHANG Lixun，WANG Keyi，et al.Dynamic modeling and control of a wire-driven rehabilitation robot［J］.Journal of Harbin Engineering University，2009，30(7):811-815.

［12］余意，易建强，李成栋，等.绳索牵引自动水平调节机器人综合控制策略［J］.电机与控制学报，2009，13(9):891-896.YU Yi，YI Jianqiang，LI Chengdong，et al .Synthetic control strategy for a cable-driven auto-leveling robot［J］.Electric Machines and Control，2009，13(9):891-896.

［13］王克义，张立勋，孟浩.1R2T绳索牵引并联康复机器人的绳索弹性研究［J］.南京理工大学学报:自然科学版，2010，34(5):602-607.WANG Keyi，ZHANG Lixun，MENG Hao.Study on elasticity of 1R2T wire-driven parallel rehabilitation robots［J］.Journal of Nanjing University of Science and Technology:Natural Science，2010，34(5):602-607.