Comparative Analysis of Vortex Induced Nonlinear Vibration of Casing Pipe under Three Different Boundary Conditions
2011-06-22
(School of Naval Architecture and Ocean Engineering,Jiangsu University of Science and Technology,Jiangsu Zhenjiang 212003,China)
Comparative Analysis of Vortex Induced Nonlinear Vibration of Casing Pipe under Three Different Boundary Conditions
GUAN Yi-feng,GU Jia-yang
(School of Naval Architecture and Ocean Engineering,Jiangsu University of Science and Technology,Jiangsu Zhenjiang 212003,China)
The casing pipes are widely used for drilling wells in the ocean.But less investigation on VIV excited by wave-current combination was done for casing pipes in the deep water.In this paper,the vortex-induced nonlinear vibration of casing pipes in deep water was studied considering the loads of current and combined wave-current.The vortex-induced vibration equation of casing pipes was set up with considering the beam mode and Morison’s nonlinear fluid damp as well as the vortex-excited loads under three different boundary conditions.The vortex-excited nonlinear vibration was calculated by using Galerkin’s method.The response including primary resonance induced by current and the composite resonance under combined wave-current for the marine drilling risers of the Donghai 3 were studied.The numerical results show that the dynamic response of marine risers induced by the current is basic and the influence of wave may be neglected.The vortex-induced nonlinear vibration of casing pipes under three different boundary conditions is studied and the complicated response behaviors of casing pipes are described under combined wave-current based on the numerical simulations.
vortex induced vibration(VIV);casing pipes;nonlinear fluid damping;lock on
Biography:GUAN Yi-feng(1966-),male,associate professor of Jiangsu University of Science and Technology,E-mail:gyf001@tom.com;GU Jia-yang(1979-),male,lecturer.
1 Introduction
The casing pipes are widely used for drilling wells in the ocean.With water depth over and above 100m,the relative stiffness of a casing pipe is reduced and the natural frequency of a casing pipe may be close to shedding frequency of vortex,so the resonance induced by vortex will occur.The vortex induced vibration of casing pipes in the deep water is the important component parts of fatigue cracks and the reliability assessment.
Because the diameter of casing pipe is much less than the length,so a casing pipe can be simplified into a beam model.The boundary conditions are determined by the physical model.
The interaction between the currents was discussed when the fluid flows through the cylinder,and the wake oscillator-model,correlation-model,and statistical-model were pre-sented for the prediction of dynamics response of cylinder in the uniform flow[2].Also the wake oscillation-model was employed to predict the vibration of cylinders in the non-uniform flow[2].The fluid dynamics force expressed in the square of velocity in Morison formula will lead to difficulties for solving the dynamic response,so Lyons[3]simplified the nonlinear term into linear term and the response in time domain for riser of TLP was calculated through simplifying the riser into a beam model.Considering the locking-in condition of vortex excited vibration,Bokaian[4]calculated the responses of vortex excited vibration in time domain.The riser of TLP was simplified into the simple support model,Dong[5-6]investigated the vibration of riser induced by vortex and stability of vibration due to nonlinear fluid damping force.However,it is worth studying whether the model of the simple support beam can represent the practical restrains at the top and the bottom.Therefore,Ma and Dong[7]suggested the beam model with the upper moveable support and fixed support at the bottom in order to investigate the dynamic response of a riser of TLP.However less investigation on VIV excited by the wave-current combination has been done for casing pipes in the deep water up to date.The bottom of the casing pipes is considered to the fixed support,because the casing pipes are penetrated deeply into the seabed.The upper support of the casing pipes model is usually supposed to simple support or fixed.The mechanical model of the upper support lies between the simple support and fixed based on the practical loading characteristic.The author uses the model of TLP tension legs proposed by Dong as reference.The upper of the beam is simplified into a moveable support due to the influence of the platform movement.The model does not restrict the horizontal and vertical motion of the upper part and only restricts the rotational movement of casing pipes.The proposed model in the paper is more in agreement with the practical mechanical model.The vortex-induced nonlinear vibration of casing pipes under three different boundary conditions is studied and compared based on the numerical simulations of Donghai 3.
2 Vibration equation and natural modes
2.1 Vibration equation of casing pipes
It is assumed that wave and current flow in the same direction x,and the cross-section of casing pipes is uniform.The coordinate original point is at the bottom of sea.The analytical model is illustrated in Figs.1-2,where l denotes the height of casing pipe.According to the model in Figs.1-2,the vibration equation of casing pipe can be given as follows:

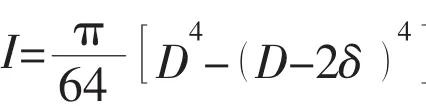
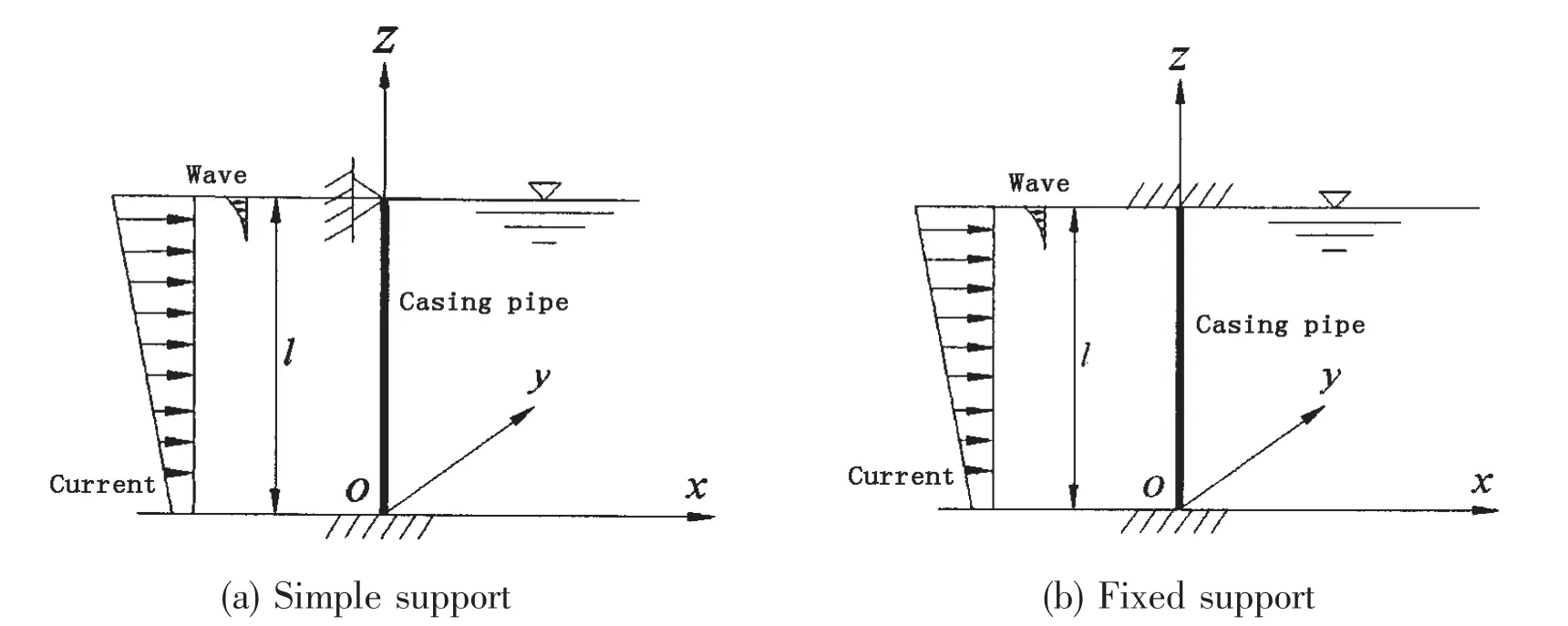
Fig.1 Costumed model of casing pipe
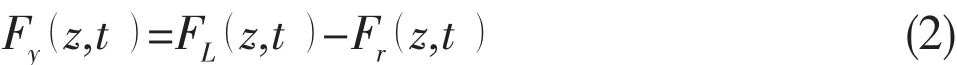
where FL(z,t)and Fr(z,t ) denote the vortex-excited force and the fluid damp force due to the motion of a casing pipe in the direction y,respectively,

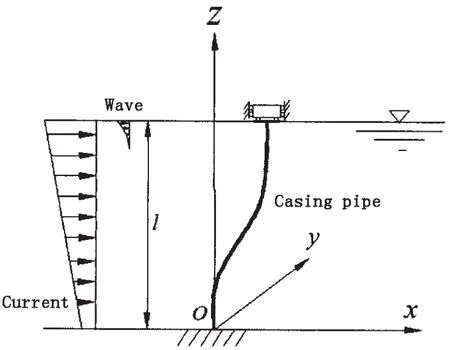
Fig.2 Model of casing pipe proposed in this paper
where ρ is the density of the fluid,CLand ωsare the lift force coefficient and the shedding frequency of vortex;u and Vcare the wave velocity in any depth of water and current velocity,respectively.
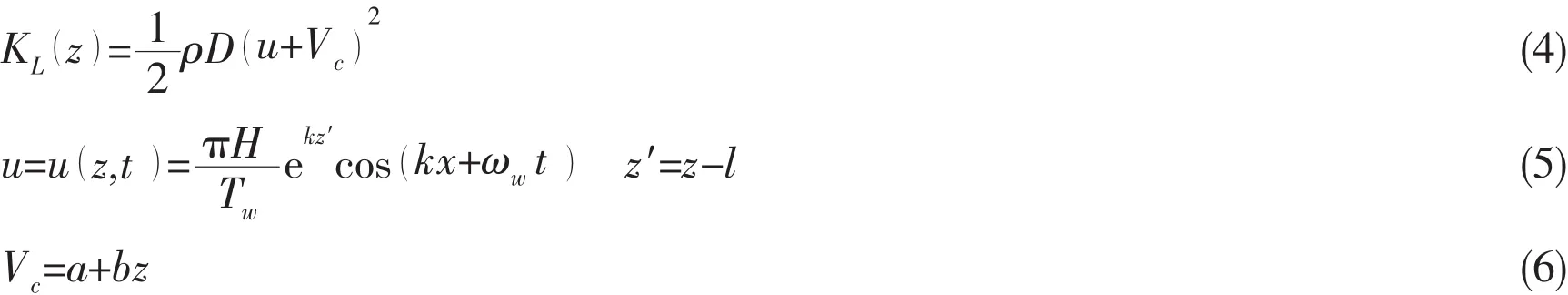
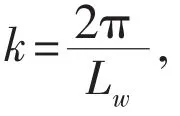
The nonlinear fluid damp force Fr(z,t ) in the direction y can be expressed in the Morison’s formula
蒸汽压与温度及物质分子脱离液体或固体的趋势有关。饱和蒸汽压P*常与温度T呈非线性的关系,可由克劳修斯- 克拉佩龙方程进行推导,经过推导得到金属饱和蒸汽压随温度变化的关系,如式(1)所示。

According to Korolov function the dynamic deflection can be expressed as follows:
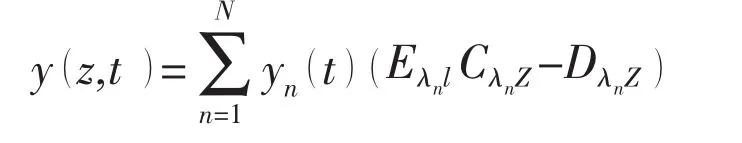
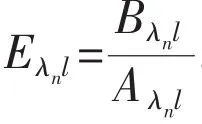
2.2 Boundary condition and natural modes of casing pipes
As for Fig.1(a),the boundary condition of casing pipe can be described as
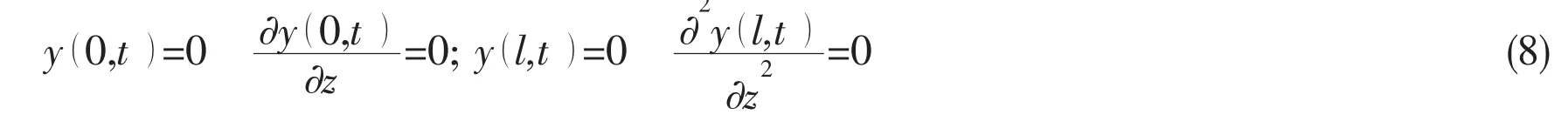
This kind of boundary condition corresponds to the bottom is fixed and the upper of the beam is simply supported.As for Fig.1(b),the boundary condition of casing pipe can be described as the fixed upper and bottom of the beam in Fig.1(b).
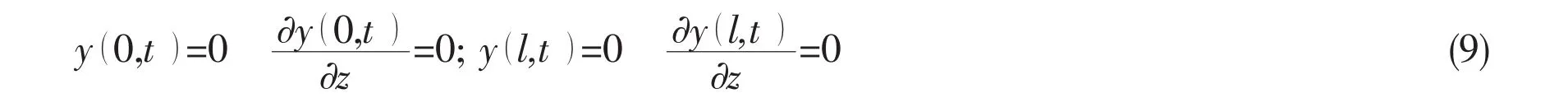
The boundary condition that is proposed in the paper can be deduced as follows:

Firstly the variable-separating method is used to solve longitudinal movement and assuming that y( z,t)=Z(z) T(t),where Z(z)is the vibration mode function,the Z(z)can be expressed as in this paper

where λ is determined by the equation of natural frequencies.Z0,Z0′,M0and Q0are the deflection,angle displacement,bending moment and shearing force,respectively.Aλz,Bλz,Cλzand Dλzare Korolov function.
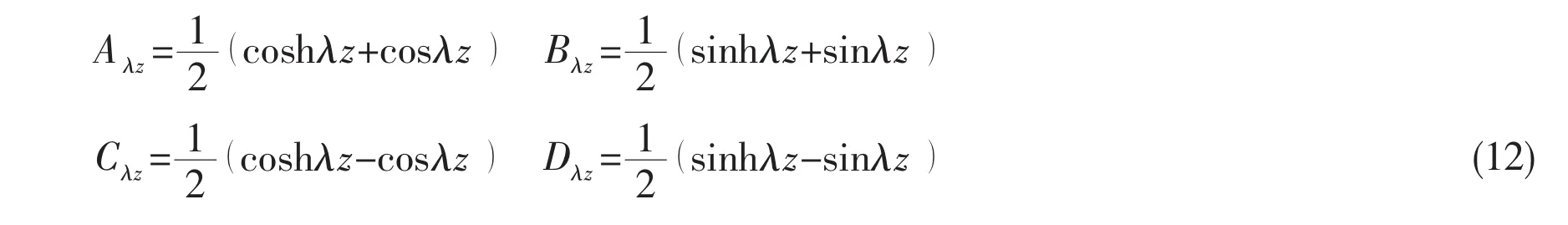
The vibration mode equations under three different boundary conditions are given as follows:
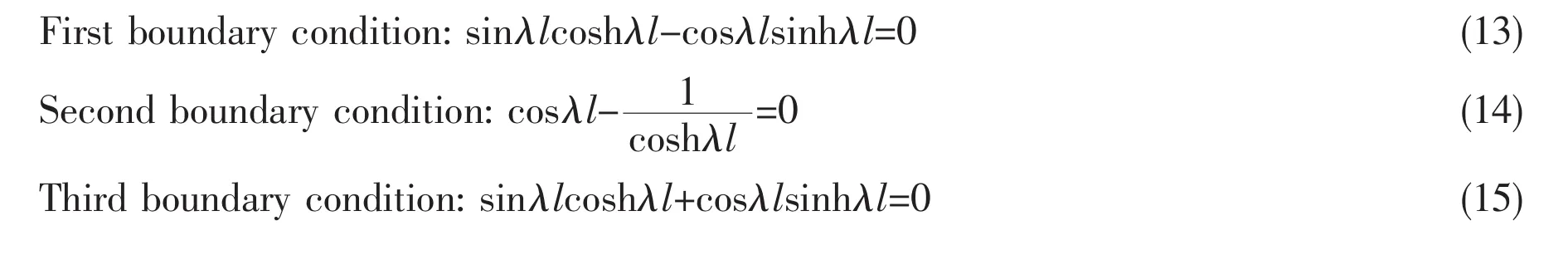
The natural frequencies λ1,λ2,…,λnare obtained using numerical method based on above equations.
Using the modes expressed by using Korolov function,the dynamic displacement is expansioned as[7]:
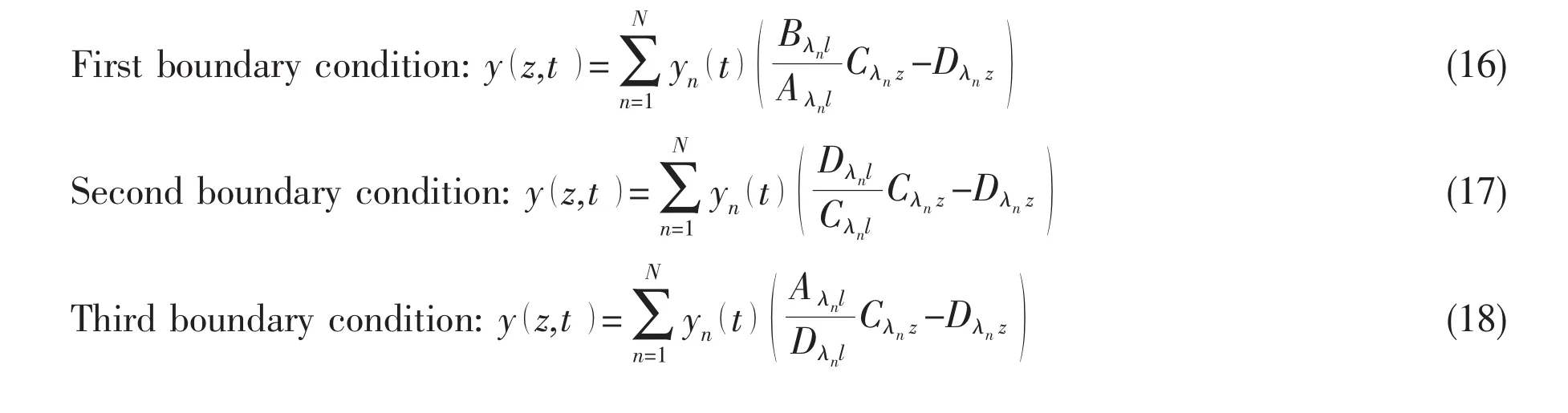
3 Solution to the differential equation of casing pipe
When solving the differential vibration equation of casing pipe,the third boundary condition is chosen as an instance,and the solutions for the other two boundary conditions are the same.
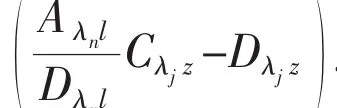
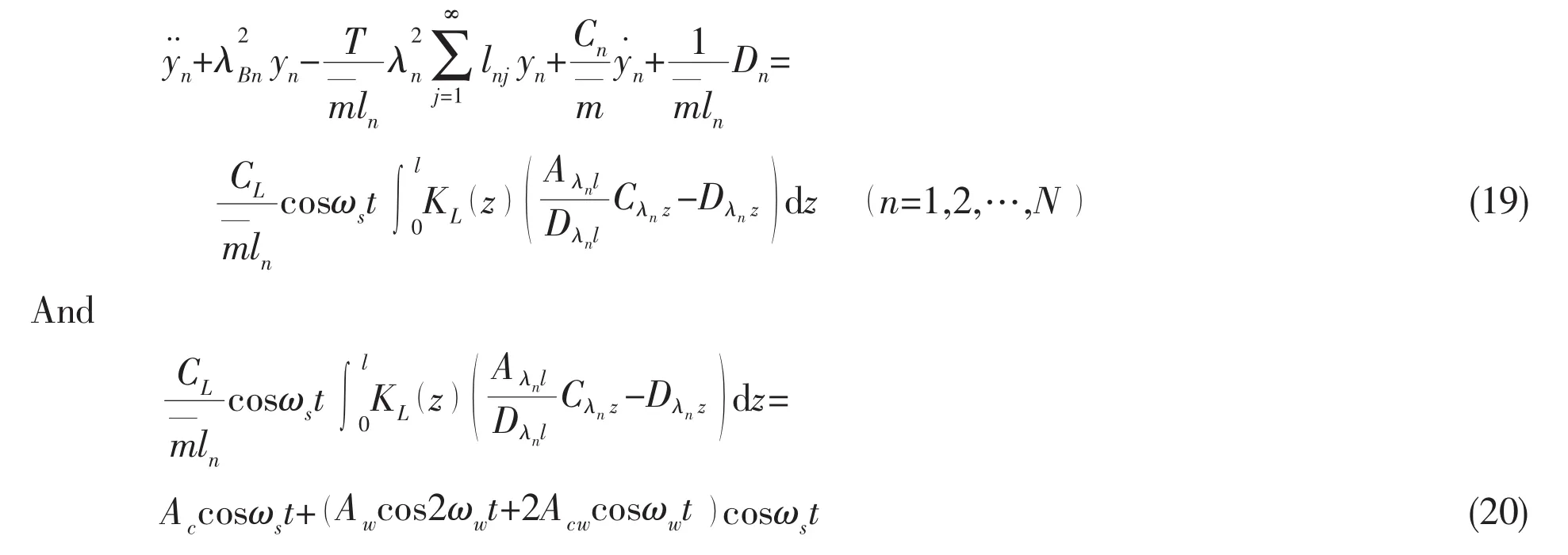
where Acand Awdenote the effects of fluid and wave,respectively,and Acwshows the coupled effects between wave and fluid,ωwis the wave frequency;=m+m′,Cn=2λBnζs,where ζsis the structural damp ratio,and
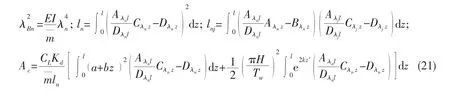

The dynamic response can be obtained by the numerical integration of Eq.(19).The sign of(z,t)will change with time t and position z in Dn,so sgnat(i+1 )step is determined by the(z,t ) at i step,and Dis solved by the numerical integration at different time
nand different height.
The bending moment M( z,t ) and shearing force can be expressed as:

4 Example
The Donghai 3 is taken as an example to simulate the dynamic response of casing pipe(Figs.3-7).
The parameters of the example are as follows:a=0.4m/s;b=0.001 286m/s;wave height Lw=150m;wave frequency ωw=0.437/s;length of the casing pipe is L=200m;diameter D=0.533 4m;thickness of wall δ=0.012 7m;density of steel ρs=7.8×103kg/m3;structural damp ration ξs=1.8×10-3;and mean axial tension of casing pipe T=2.490×105N.The wet natural frequencies of the casing pipe considering added water were calculated,and shown in Tab.1.

Tab.1 Natural frequencies
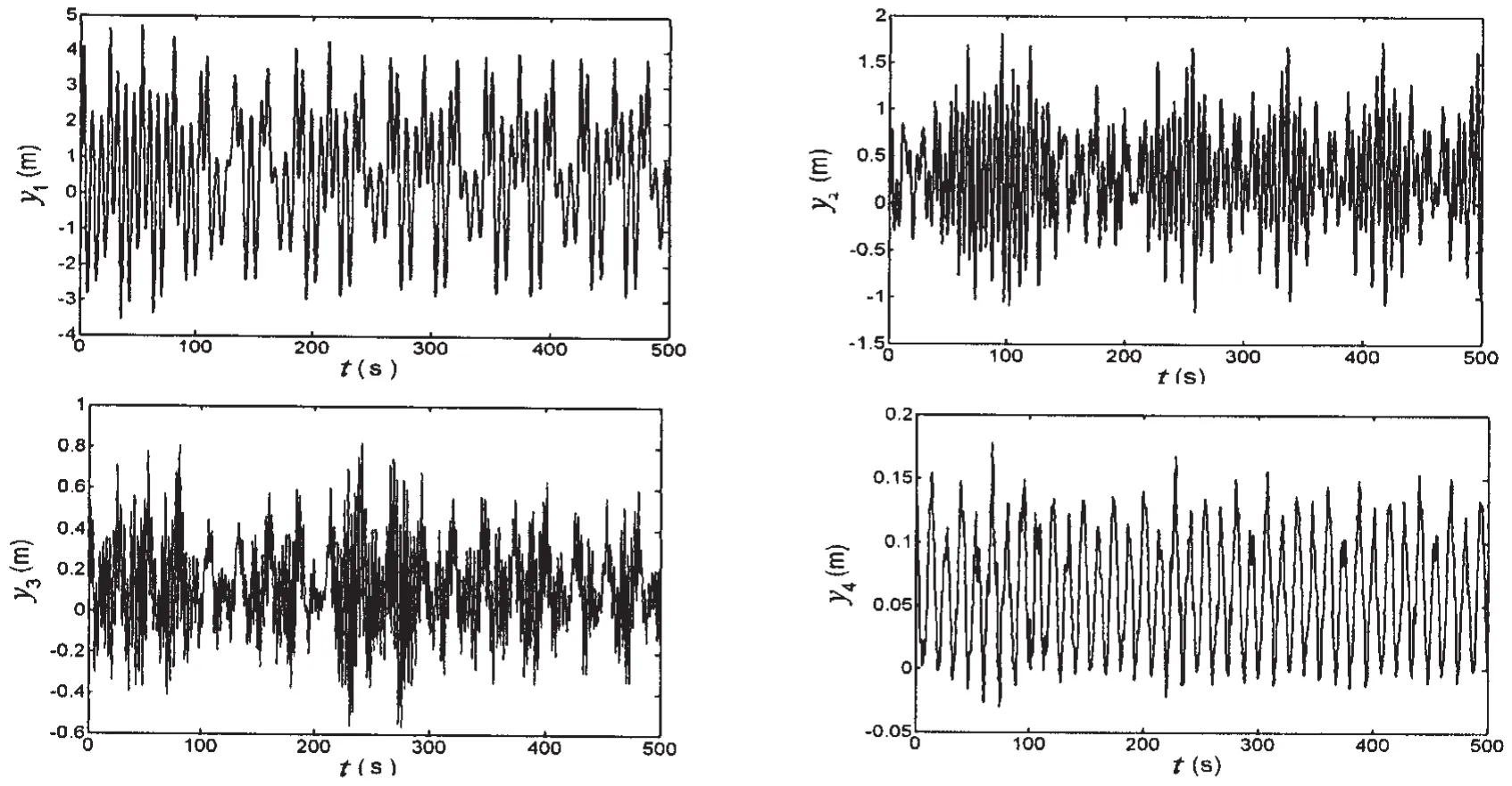
Fig.3 Dynamic response of casing pipe induced by wave-current(the first boundary condition)
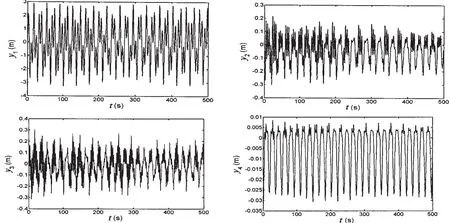
Fig.4 Dynamic response of casing pipe induced by wave-current(the second boundary condition)
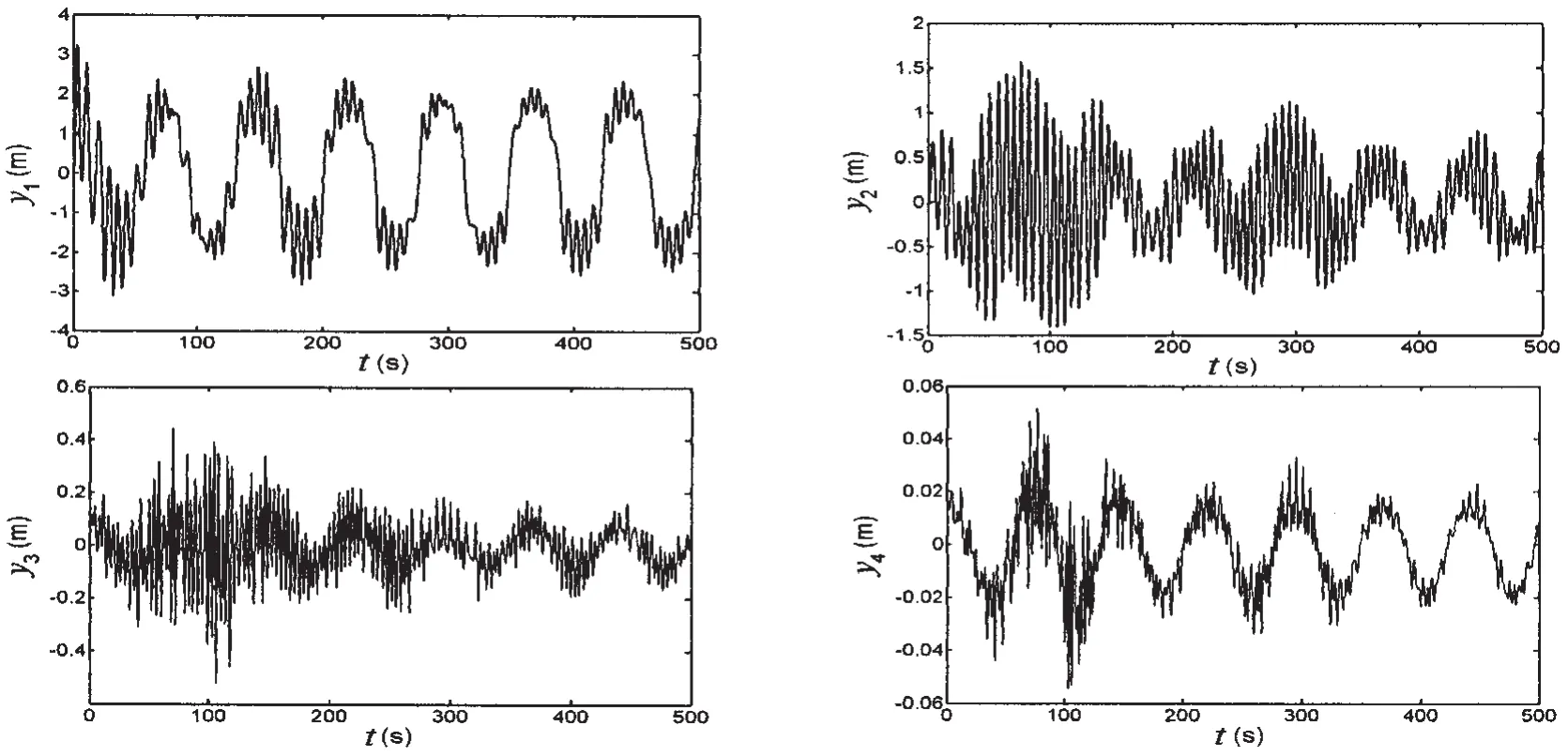
Fig.5 Dynamic response of casing pipe induced by wave-current(the third boundary condition)
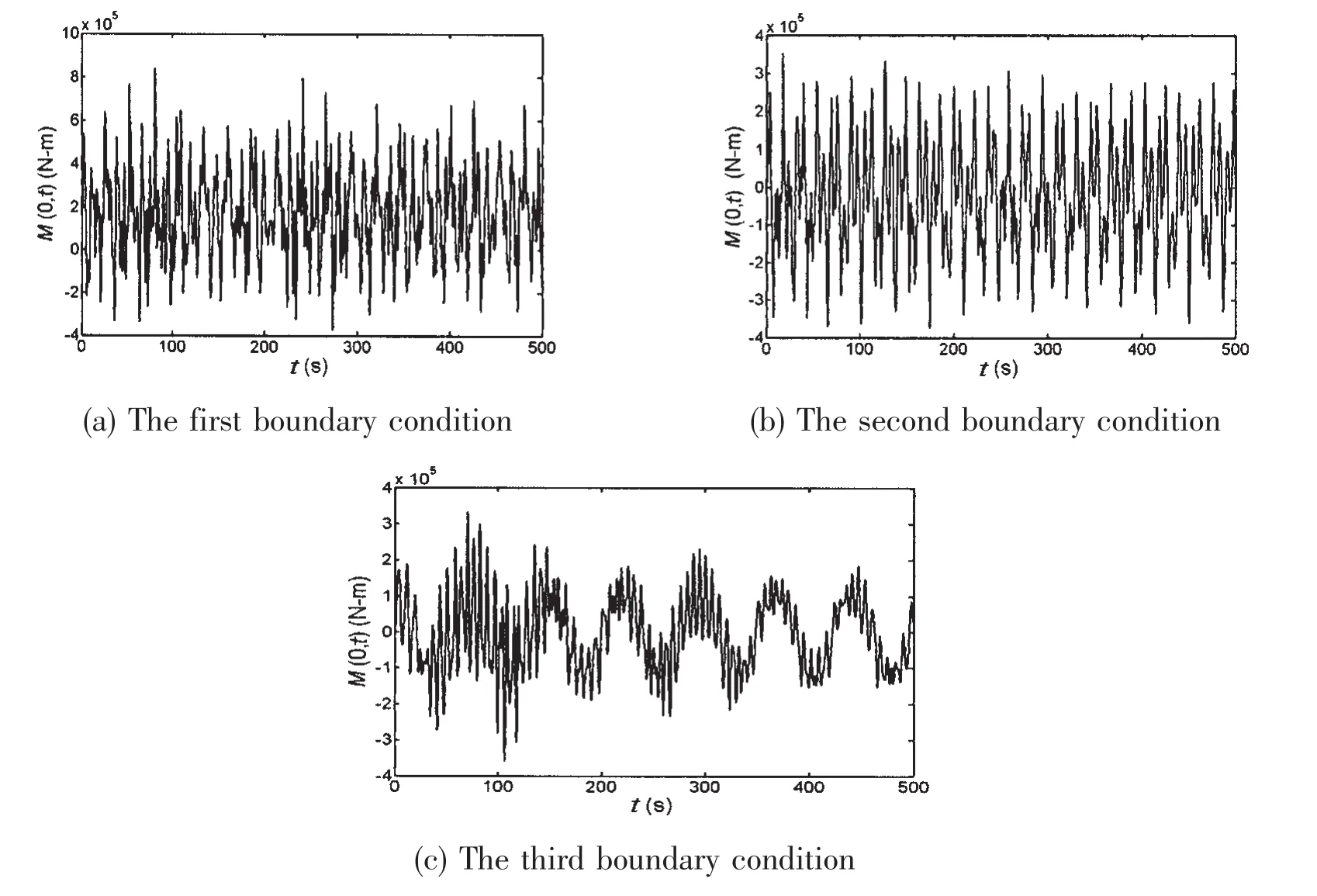
Fig.6 Bending moment response in the seabed
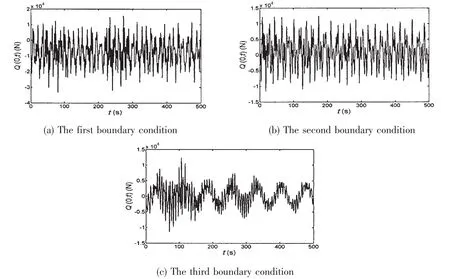
Fig.7 Shearing force response in the seabed
5 Conclusions
The vortex-induced nonlinear vibration differential equation of casing pipes in the deep water was set up by considering the Morison nonlinear fluid loads and vortex-induced loads under three different boundary conditions.The Donghai 3 was taken as an instance to study the dynamic response and inner force response for different boundary conditions.Some conclusions are drawn:
(1)The differential equation is set up by considering the loads of wave and current,but in the numerical simulation we found that the dynamic response induced by wave can be neglected(the Airy wave is used in this paper).The dynamic response is induced mainly by current.
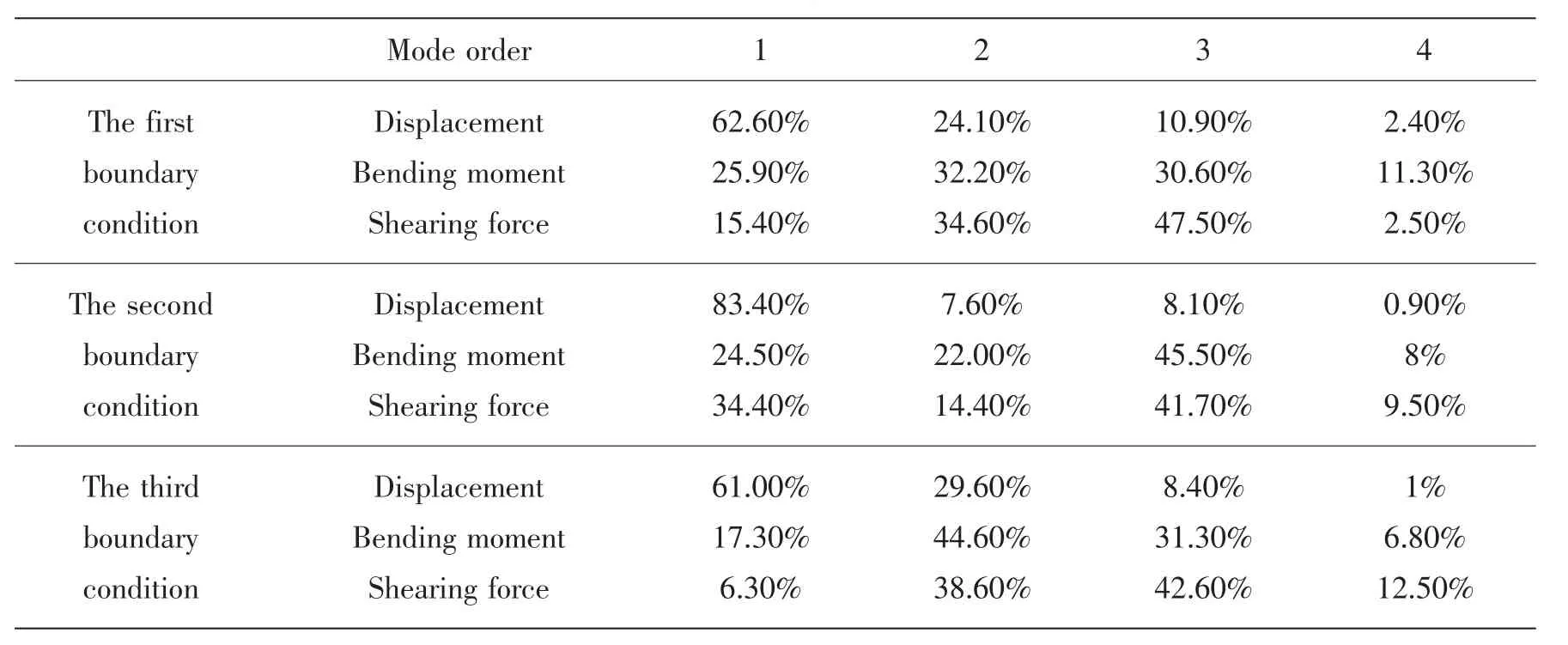
Tab.2 Percent of dynamic response amplitude at the seabed for every mode
(2)From the Tab.2 it can be found that the displacement responses of the first three modes are about 98%of total response,but bending moment and shearing force of the first three modes are about only 90%.The orders of dynamic response for bending moment and shearing force have to be increased if we want to obtain the same precision as displacement response.
[1]Sparpkaya T.Vortex-induced oscillation:A selective review[J].Journal of Applied Mechanics,1979,46(2):241-248.
[2]Iwan W D.The vortex-induced oscillation of non-uniform structural system[J].Journal of Sound and Vibration,1981,79(2):291-301.
[3]Lyons G J,Petal M H.A prediction technique for vortex induced transverse response of marine riser and tethers[J].Journal of Sound and Vibration,1986,111(3):467-487.
[4]Bokaian A.Lock-in prediction of marine riser and tethers[J].Journal of Sound and Vibration,1994,175(5):607-623.
[5]Dong Yanqiu,Xie Geng,Lou J Y K.Stability of vortex-induced oscillation of tension leg platform tethers[J].Ocean Engineering,1992,19(6):551-571.
[6]Dong Yanqiu.Vortex-excited nonlinear vibration of tension leg of ocean platform in wave and current[J].Acta Oceanologica Sinica,1994,16(3):121-129.
[7]Ma Chi,Dong Yanqiu,Hu Zhimin.Vortex-induced nonlinear response of TLP[J].Journal of Tianjin University,2000,33(6):701-706.
[8]Ding Xuecheng.Structural dynamics[M].Beijing:Higher Education Press,1992:135-145.
三类边界条件下隔水套管涡激非线性振动的分析研究
管义锋,谷家扬
(江苏科技大学 船舶与海洋工程学院,江苏 镇江212003)
考虑流及波流联合作用,研究了套管的涡激非线性振动.将套管简化为梁模型,考虑3类不同的边界条件,计及莫里森非线性流体动力和涡激荷载,建立套管的涡激振动方程。应用克雷洛夫函数求解套管的固有频率和模态,采用了计算涡激非线性动力响应的迦辽金方法。以东海勘探3号钻井隔水套管为例,研究了不同边界条件下流引起的主共振和波流联合引起的组合共振。计算结果表明:流对套管的动力响应占主导地位,而波的影响不大。分析了3类不同边界条件下隔水套管的涡激非线性动力响应,揭示了波流联合激励下套管复杂的动力响应特性。
涡激振动;隔水导管;非线性流体阻尼力;谐振
O321
A
管义锋(1966-),男,江苏科技大学副教授;
谷家扬(1979-),男,江苏科技大学讲师。
O321
A
1007-7294(2011)12-1384-10
date:2011-02-01
猜你喜欢
杂志排行
船舶力学的其它文章
- Numerical Research on Ventilated Supercavity Shape and Flow Structure in the Turning Motion
- A Comparative Investigation on Optimization of Propeller Blade Section Design
- Experimental Investigation of Sloshing Loads and Structural Dynamic Responses in Tanks of LNG Carriers
- Study of Damage Characteristics during Fatigue by Acoustic Emission Techniques
- Nonlinear Model for Vibration Analysis of Fluid-conveying Pipes via the Incremental Harmonic Balance Method
- Coupled Vibration of Fluid-filled Functionally Graded Material Cylindrical Shell
