大功率船用齿轮箱传动系统和结构系统耦合特性分析

朱才朝，陆 波，徐向阳，王海霞

（重庆大学机械传动国家重点实验室，重庆 400030）

大功率船用齿轮箱传动系统和结构系统耦合特性分析

朱才朝，陆 波，徐向阳，王海霞

（重庆大学机械传动国家重点实验室，重庆 400030）

船用齿轮箱是船舶轮机系统的重要组成部分，其动态性能的好坏直接影响系统的性能，因而开展船用齿轮箱动态特性研究具有重要的意义。文章对某大型船用齿轮箱的固有特性进行分析，通过轴承支撑把传动子系统和结构子系统两者耦合起来，建立齿轮—转子—轴承—箱体耦合系统动力学模型。采用有限元软件中的Lanczos方法对齿轮箱系统固有特性进行了计算，得到固有频率及其振型，通过分析齿轮系统的激励频率，得出传动级离合器齿轮在工作过程中造成了较大的振动和噪音，与实际相符。

船用齿轮箱；耦合振动；固有特性；模态分析；有限元

1 引 言

大功率船用齿轮箱装置是船舶轮机系统的重要设备之一，其结构复杂，精度要求很高，且处于重载的运行条件下，综合技术指标远远高于其它船用齿轮箱。重载齿轮在传动过程中产生较大的振动、噪声和动载荷，有可能导致系统某些环节的失灵或损坏，甚至会导致齿轮系统本身的破坏和故障等。因此，开展船用大功率齿轮箱动态特性分析，控制齿轮箱系统的振动与噪声，实现船用齿轮系统的动态设计己成为重要的研究课题。

目前关于齿轮箱系统的研究主要集中在齿轮—转子系统动态特性以及齿轮箱体优化减重分析上，而通过轴承连接把齿轮—转子系统和箱体系统作为一个整体进行研究涉及较少[1-5]。论文通过建立大功率船用齿轮箱动力学模型，采用有限元软件中的Lanczos算法对系统固有特性进行计算，确定齿轮箱系统的模态参数,包括模态固有频率和振型，在实际工作中可利用模态参数结果进行故障判别，使其日益成为一种有效的故障诊断和安全检测的方法。

2 大功率船用齿轮箱基本结构及传动原理

大功率船用齿轮箱具有倒顺、离合、减速和承受螺旋桨推力的功能，与主机配套，组成船用动力机组。其工作过程分别沿顺车、倒车两条线路执行，齿轮箱的传动简图如图1。

轴Ⅰ为输入轴，轴Ⅱ、Ⅵ分别为顺车、倒车传动轴，轴Ш、Ⅴ分别为顺车、倒车齿轮轴，轴Ⅳ为输出轴，整个结构为空间啮合传动。实际工作中输入扭矩经输入轴Ⅰ传递到顺车传动轴Ⅱ，顺车时，摩擦离合器2摩擦片贴紧，离合器内齿轮闭合，轴Ⅱ与轴Ш连接，扭矩经顺车齿轮3、输出齿轮4传递给输出轴Ⅳ；倒车时，扭矩经离合器2与6传到传动轴Ⅵ，摩擦离合器6摩擦片贴紧，离合器内齿轮闭合，轴Ⅵ与轴Ⅴ连接，经倒车齿轮5、输出齿轮4传递到输出轴Ⅵ。齿轮箱详细传动参数见表1。

图1 传动系统简图Fig.1 The sketch of transmission system

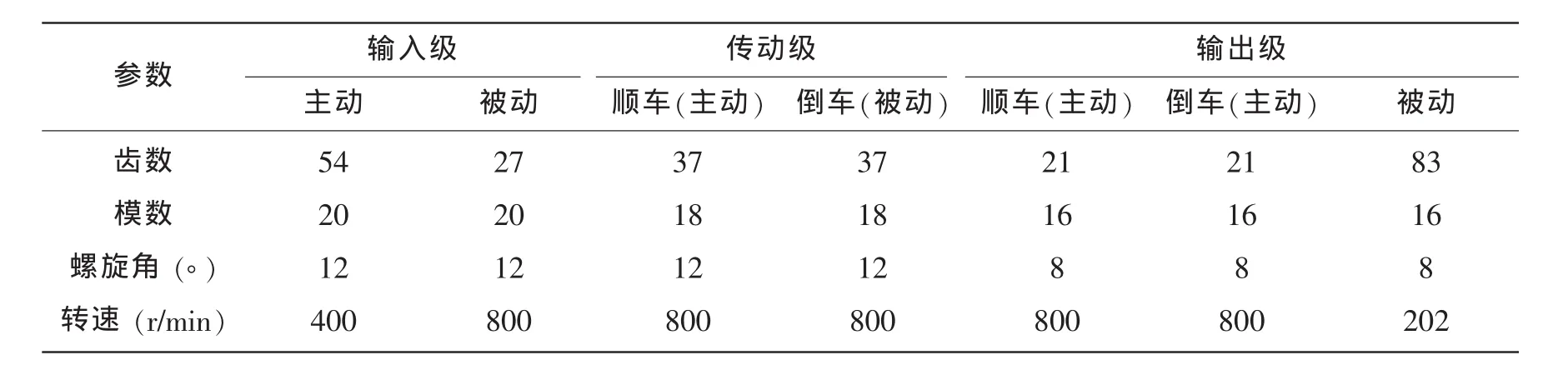
表1 大功率船用齿轮箱传动参数Tab.1 The parameters of large-power marine gearbox transmission

3 大功率船用齿轮箱系统动力学模型

将大型船用齿轮箱分为传动系统和结构系统，分别建立各子结构动力学模型，利用两个子结构之间的支撑轴承，将系统耦合起来，建立整个齿轮箱耦合动力学分析模型。

设下标b表示结构子结构，下标g表示传动子结构，则可得

式中：Fg{}，Fb{}为传动子系统和结构子系统力向量；mg{}，mb{}为传动子系统和结构子系统质量矩阵；cg{}，cb{}为传动子系统和结构子系统阻尼矩阵；kg{}，kb{}为传动子系统和结构子系统刚度矩阵；xb{}，xg{}为传动子系统和结构子系统位移向量。

4 大功率船用齿轮箱三维有限元模型

根据齿轮几何参数，将加工齿轮所用刀具的参数代入端面渐开线方程和端面齿根过度曲线方程中，逐点计算出齿轮的端面渐开线和齿根过渡曲线上各点在总体坐标系O-xy（）z中的准确坐标值。

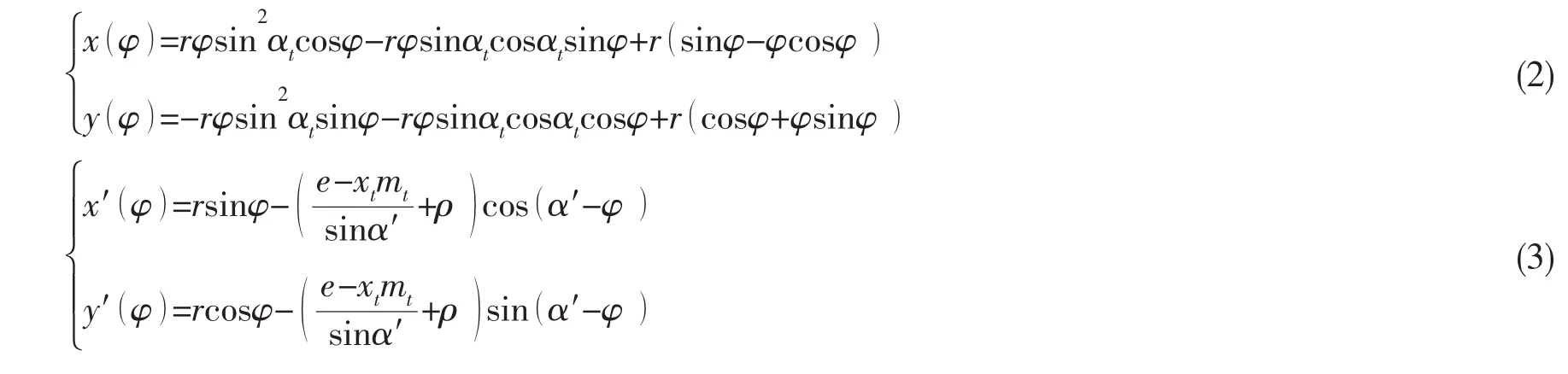
根据上式计算出轮齿端面渐开线和齿根过渡曲线上不同点的坐标，进而构建出齿面轮廓。将齿轮箱传动系统几何参数代入上述方程，得出各齿轮齿面轮廓，构造出轮齿实体几何模型。根据内外齿轮的各参数，采用Pro/engineer软件根据图纸绘制三维几何模型如图2。

图2 齿轮箱实体装配模型Fig.2 Gearbox entity assembly model

齿轮箱体的结构比较复杂，机体上分布有筋板、凸台、轴承孔和各螺栓联接孔等，在建立有限元模型时，采用自由网格划分方法，用八节点四面体实体单元，对齿轮箱体进行了有限元网络划分；齿轮、顺倒车油缸、轴通过拉伸、扫略、镜像等方法采用八节点六面体实体单元。网格划分在专业前处理软件hypermesh中完成,共划分为411 099个单元，526 219个节点，如图3所示。

图3 齿轮箱体网格模型Fig.3 Gearbox mesh model

齿轮箱在实际安装中是用四个螺栓联接到机架的，箱体的边界条件取为箱体底平面的垂直方向约束、螺栓连接处固定约束。传动系统齿轮间定义接触边界条件，法向接触特性为硬接触，切向接触特性为库伦摩擦，摩擦系数为0.05；箱体、轴之间用弹簧模拟轴承，弹簧在圆柱坐标下定义径向和轴向刚度。

船用齿轮箱共10个滚动轴承，2个滑动轴承、2个推力轴承。分析中，滑动轴承和滚动轴承用弹簧单元进行模拟。在圆柱坐标下，采用点面耦合方法，将箱体、轴与轴承实际接触面分别耦合在两节点上，两节点之间添加弹簧单元模拟轴承，避免箱体、轴接触面周向对应单节点之间采用弹簧单元模拟轴承造成局部应力集中。弹簧刚度根据理论计算方法得到，弹簧刚度值见表2所示。

表2 齿轮轴轴承刚度识别结果Tab.2 The results of bearing stiffness identification

5 三维有限元模态分析

模态分析是建立在静态有限元模型基础上的，在进行模态分析时，由于求解的是系统的固有特性（固有频率和固有振型），与所受外力无关，因此可忽略外部载荷的作用；且在求结构的固有特性时，阻尼对其影响不大，阻尼项可以略去，故耦合后齿轮箱系统无阻尼自由振动的运动方程为

其对应的特征方程为

转化成标准特征值问题

式中：[K]为齿轮箱系统总刚度矩阵；[M ]为齿轮箱系统总质量矩阵；w为系统固有频率。

方程（6）是关于λ的n次方程，求解方程可得系统的n个固有频率，对应于每个固有频率可以确定一组各节点的振幅值 {xi}，从而得到结构的各阶振型。

Lanczos法是一种较新的求解模型的固有频率和振型的方法，其求解精度高，求解速度快，特别适合对大型模型的求解。Lanczos算法求解矩阵方程（6）其主要步骤如下：

（b） 迭代：迭代公式为 rj+1=Aqj-αjqj-βjqj，其中 αj=qTjAqj，qj+1=rj+1/βj+1；

（c）从理论上讲，上述迭代在没有截断误差的情况下进行下去，则q1，q2，q3…为一组正交的单位向量，Qj=（q1，q2，…，qn）即为Lanczos转换矩阵，引入右边的矩阵Tj：

Lanczos算法的前j步可表示为

其中ej为第j个单位向量，设θ和s为三对角阵Tj的一个特征对，即

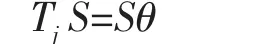
则θ和Y（ Y = Qjs）为原求解问题的一个特征对，方程变为

从而使对A的特征值求解转化为对Tj的求解。Lanczos算法的最大优点是其所得的三对角阵Tj的特征解直接近似于原矩阵A中j个特征根。因此对于求解大型结构模态问题，Lanczos法可以非常快速有效地求解。

采用ABAQUS软件中的Lanszos求解方法对齿轮箱进行约束模态求解。得到船用齿轮—转子—轴承—支承耦合系统前十阶固有频率和振型，表3给出了前20阶固有频率和振型情况，图4给出了前5阶固有振型以及关心的第22阶固有振型图（为看清内部，部分箱体单元不显示）。

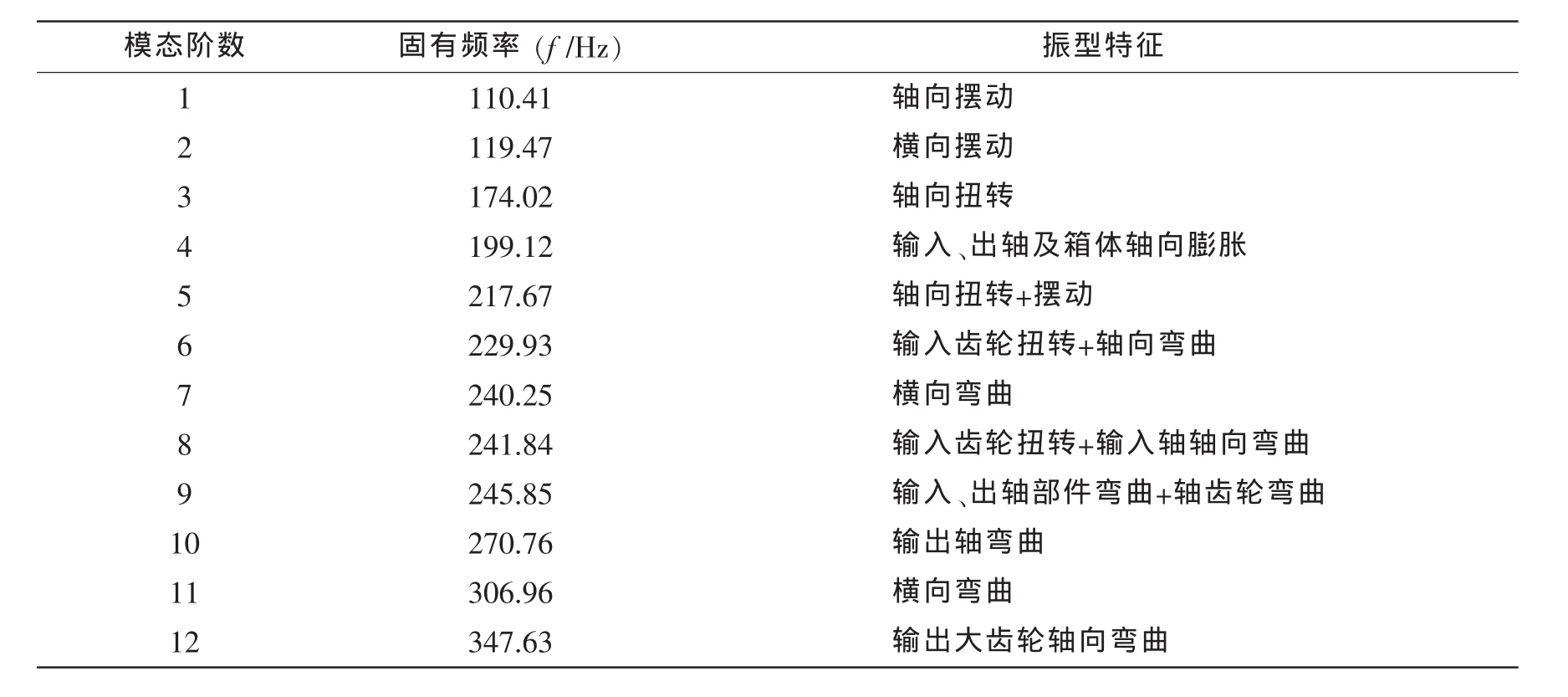
表3 齿轮箱体前20阶固有频率及振型Tab.3 The first 20-stage natural frequencies and vibration modes of the gearbox

续表3

图4 船用齿轮箱前六阶振型Fig.4 The first 6-stage vibration modes of the gearbox

该船用齿轮箱输入转速为400 r/min，其各工况下的转速和啮合频率分别为：400 r/min，360 Hz；800 r/min，493.33 Hz；202 r/min，280 Hz。与表3比较，输入级、输出级啮合频率远离系统固有频率，不产生共振现象。传动级离合器齿轮啮合频率493.33 Hz与系统第22阶固有频率499.59 Hz接近，产生共振现象，因高阶振型对结构实际振动贡献量非常小，对齿轮系统结构不产生较大的危害。这与齿轮箱在实际工作中，离合器齿轮处产生较大的振动与噪音相符。

6 结 论

建立大功率船用齿轮箱三维有限元模型，采用有限元软件中的Lanczos算法对某大功率船用齿轮箱固有特性进行了分析，得到了齿轮箱系统的固有频率和振型。结果表明整个齿轮箱系统的振型较为复杂，表现为箱体以及内部齿轮间复杂扭转、平移、摆动、弯曲等，且方向、幅度等均不同；各阶固有频率比较密集,这与其复杂的结构有关；输入级、输出级啮合频率远离系统固有频率，不产生共振现象，传动级离合器齿轮啮合频率与系统某高阶固有频率接近，产生共振现象，造成离合器齿轮处产生较大振动与噪音。论文通过对齿轮箱系统固有特性的研究，直观地分析齿轮系统的动态特性和薄弱环节，为进一步系统研究齿轮系统动态性能打下了基础。

[1]陶泽光.齿轮系统有限元模态分析[J].机械设计与研究,2000,28(3):45-46.

[2]杨成云.中心传动齿轮箱体固有特性研究[J].机械设计与制造工程,2002,31(4):26-28.

[3]王立华.斜齿圆柱齿轮传动系统的耦合振动分析[J].机械设计与研究,2002,18(5):30-32.

[4]王 基.某型船用传动齿轮箱振动模态的试验与分析[J].海军工程大学学报,2007,19(2):55-59.

[5]李 明.DH型压缩机组齿轮联轴器耦合轴承—转子系统的动力学研究[J].机械强度,1999,21(3):166-170.

[6]李润方.齿轮系统动力学[M].北京:科学出版社,1997.

Analysis of coupling characteristic of transmission and structure system of large-power marine gearbox

ZHU Cai-chao,LU Bo,XU Xiang-yang,WANG Hai-xia

(State Key Laboratory of Mechanical Transmission,Chongqing University,Chongqing 400030,China)

The research on dynamic characteristics of the gearbox is of great significance to the marine engine system.In this paper,the natural characteristic of large marine gearbox is investigated.A coupling system(gear-rotor-bearing-box)dynamics model is established by coupling transmission subsystem and structure subsystem with the support of bearing.By using Lanczos method,natural frequencies and vibration models are obtained.By the analysis of caparisoning the gear wheel excitation frequencies with the result,it is proved the fact that transmission stage clutch gear causes large vibration and noise in its operation,which matches practical case.

marine gearbox;coupling vibration;natural characteristic;modal analysis;finite element analysis

TH123

A

1007-7294（2011）11-1315-07

2011-03-24

国家十一五科技支撑计划资助项目（2006BAF01B07-01）；新世纪优秀人才计划（NCET-05-0766）资助项目

朱才朝（1967-），男，博士后，教授，博士生导师。主要从事传动系统动力学及振动噪声

预估与控制的研究，E-mail:zcc92@163.com。