长江下游镇江至吴淞段潮位相关途径预报方法
2011-06-19林刚毅程文辉
朱 琰,水 艳,林刚毅,程文辉
(河海大学水文水资源学院,江苏南京 210098)
长江下游镇江至吴淞段潮位预报问题通常可以采用两种途径来解决:一是通过水动力学方法[1],即取大通断面流量作为长江下游干流的上边界条件,取吴淞口(南支)及三条巷(北支)潮位为下边界条件,并假定大通以下没有大支流汇入,除了与太湖流域有水量交换外,假定与其他地区无水量交换进行计算.该方法由于缺乏大量的长江下游干流实测大断面资料以及不考虑区间的水量交换,使得计算断面的水位精度较低[2].二是通过相关途径方法预报沿江潮位.为了使相关分析的物理概念比较清晰,将沿江潮位分解为两部分,一部分受上游大通流量影响[3],另一部分受下游吴淞口潮汐影响.本文利用吴淞口天文潮位预报结果[4-10]和大通站日平均流量,通过相关途径方法来预报沿江各站整点潮位过程.
1 日平均水位相关分析
通过分析沿江各潮位站断面日平均水位的影响因素,建立日平均水位的相关方程.
1.1 日平均水位与大通流量的相关关系
计算镇江至吴淞口沿江各潮位站断面的日平均水位,该水位基本上滤掉了吴淞口潮汐影响.1999年6月1日至8月31日镇江、江阴、浒浦、七浦和吴淞口沿江5个站的日平均水位及大通流量过程如图1所示.
由图1可见,越是上游潮位站受长江上游来水影响越大.采用多元线性回归分析建立各断面日平均水位与大通流量的相关关系,则多元线性回归方程为
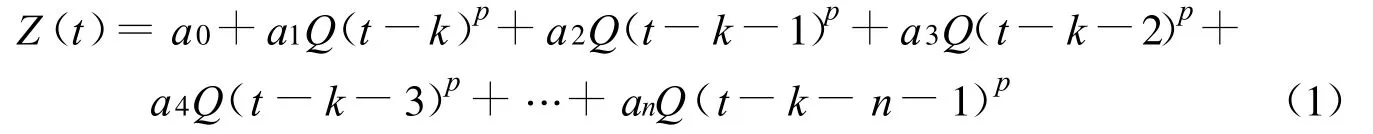
式中:Z(t)——某站日平均水位,m;Q——大通站流量,m3/s;t——时间,d;ai(i=1,2,…,n)——系数;k——滞后时间(因为大通站流量需要一定的传播时间才能影响本断面水位),d;n——采用的相关天数,d;p——指数,因为流量与水位之间不是线性关系.
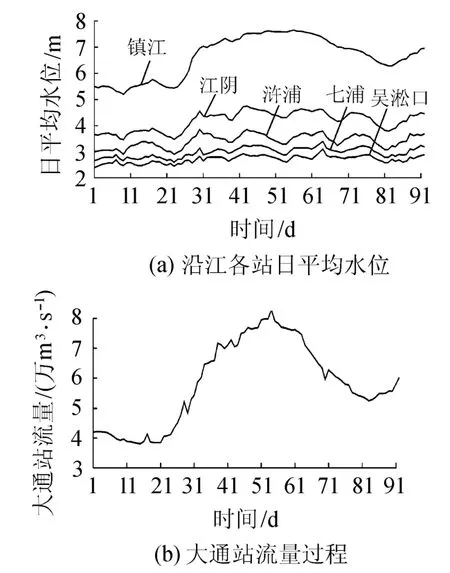
图1 5个站的日平均水位与大通站流量过程Fig.1 Daily average water level at five stations and discharge of Datong Station
经初步优化分析决定采用参数为:k=2d;n=4 d;p=0.05.相关方程式(1)中各站的相关系数如表1所示.
1.2 相关方程式(1)的精度
根据上述的参数和相关系数,计算沿江各站的日平均水位,并与实测日平均水位比较,如图2所示.
各站的计算日平均水位与实测水位之间的均方差及相关系数分别为:镇江0.187m和0.970,江阴0.170m和0.874,浒浦0.178m和0.666,七浦0.111m和0.789,吴淞口0.187m和0.762.
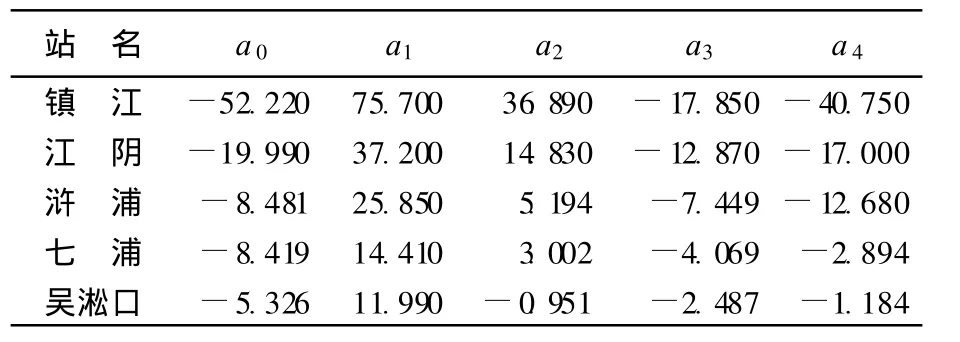
表1 相关方程式(1)中各站的相关系数Tab le 1 Correlation coefficients in Eq.(1)for five stations

图2 沿江各站计算(式(1))与实测日平均水位过程Fig.2 Calculated(through Eq.(1))and measured daily average water levels at five stations
1.3 影响日平均水位的其他因素
从图2和各站的计算日平均水位与实测水位之间的均方差及相关系数可见,沿江各站日平均水位与大通流量的关系以镇江最为明显,相关系数亦最高,向下游相关系数逐渐减小,但浒浦站例外.特别值得注意的是吴淞口日平均水位与长江来水有一定的相关关系,吴淞口的水位不完全受天文潮[10-12]的影响.从七浦、浒浦、江阴日平均水位过程线可以发现有明显的周期约为14 d的波动,与大、小潮有关.为此,将上述3站潮位过程与日平均水位绘在同一图上,如图3所示.
由图3可见,大潮期间日平均水位高,小潮期间日平均水位低.这是因为,大潮时潮流量大,落潮时水面比降大,潮位过程的低潮位区抬高而引起日平均水位抬高之故.
吴淞口站主要受天文潮影响,镇江站潮流量已不大,因此大、小潮对日平均水位影响不明显.
显然,沿江各站日平均水位除了与上游大通站流量有关外,还与吴淞口天文潮的大小有关.因此相关方程(1)中需要增加能反映潮差大小的相关因子,变为

图3 各站潮位过程和日平均水位Fig.3 Tidal levels and daily average water levels at five stations

式中,F(t)为能反映t时刻潮差大小的一个因子.由于潮汐自吴淞口传播到浒浦约3h,到江阴约4h,到镇江有8~10h,因此只取当天的潮差因子.
可以取当天的潮差作为F(t),亦可以取其他类似的指标作为F(t),例如:

式中:Zj——吴淞口整点潮位,m;Z0——吴淞口日平均水位,m.
本文取方程(3)作为F(t)指标.相关方程式(2)中各站的相关系数如表2所示.
1.4 相关方程式(2)的精度
根据表2中的相关系数,计算沿江各站日平均水位,并与实测日平均水位比较,如图4所示.

表2 相关方程式(2)中各站的相关系数Table 2 Correlation coefficients in Eq.(2)for five stations

图4 沿江各站计算(式(2))与实测日平均水位过程Fig.4 Calculated(through Eq.(2))and measured daily average water levels at five stations
由图4可见,相关方程中增加反映潮差因子后精度有明显提高.从图4可以发现吴淞口日平均水位与长江干流的径流量及大小潮有关,并非纯粹的天文潮.各站的计算日平均水位与实测日平均水位之间的均方差及相关系数分别为:镇江0.161m和0.978,江阴0.085m和0.971,浒浦0.079m和0.944,七浦0.073m和0.915,吴淞口0.073m和0.834.
2 潮差相关分析
吴淞口潮汐向上游传播时,会产生潮差减小、位相后移、潮汐变形,即涨潮变陡、落潮变平缓等水力现象.上游某站的潮差大小,首先与吴淞口潮差大小有关,其次是长江干流的流量.显然,长江干流流量越大,潮差衰退越快.因此,上游某站的潮差可用以下相关方程表示:
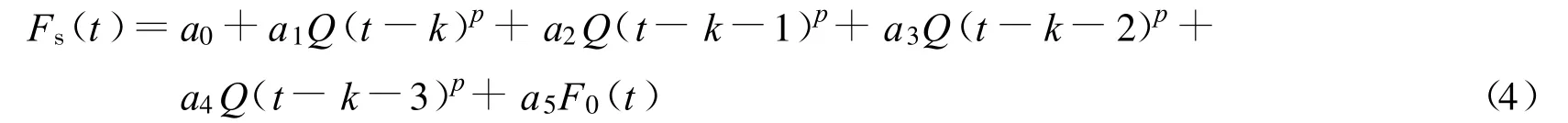
式中:Fs(t)——上游某站潮差,m;F0(t)——吴淞口潮差,m.经初步优化分析,采用参数为:k=2d;n=4d;p=0.25.
相关方程式(4)中各站的相关系数如表3所示.

表3 相关方程(4)中各站的相关系数Tab le 3 Correlation coefficients in Eq.(4)for five stations
根据上述的参数和系数,计算沿江各站潮差,并与实测日潮差比较,如图5所示.各站的计算潮差与实测潮差之间的均方差及相关系数分别为:镇江0.069m和0.964,江阴0.068m和0.996,浒浦0.127m和0.975,七浦0.057m和0.996.

图5 沿江各站计算(式(4))与实测潮差过程Fig.5 Calculated(through Eq.(4))and measured tidal ranges at five stations
3 潮汐传播时间分析
潮汐向上游传播时高潮传播时间略短,低潮传播时间略长,因此引起潮汐变形,潮汐越向上游,涨潮历时越短,落潮历时越长.但对沿江口门引排水而言,重要的是平均水位和潮差.为了简单起见,不考虑潮汐变形,潮汐传播时间亦取整点值,潮汐传播时间分别为:吴淞口至七浦为1h,七浦至浒浦为1h,浒浦至江阴为2h,江阴至镇江为4h.
4 沿江各站潮位过程预报
综上所述,根据吴淞口天文潮调和常数计算出吴淞口整点天文潮位过程线.吴淞口日平均水位受长江来水和潮差影响,因此取反映海平面平均水位的常数项为零,仅计算潮汐过程.根据式(3)计算吴松口潮差指标F(t),根据相关方程式(2)计算沿江各潮位站日平均水位,根据相关方程式(4)计算沿江各潮位站潮差,过程线形状借用吴淞口天文潮位过程,得各潮位站“天文潮位”过程.将各潮位站平均水位与“天文潮位”过程叠加得沿江各潮位站整点潮位过程.根据传播时间将各潮位站的整点潮位过程向后推移,即得沿江各站的预报潮位过程线.
5 结 语
由于长江下游镇江至吴淞段潮位受潮汐和长江上游径流量影响,对于沿江各站潮位预报问题,吴淞口潮位预报是关键的一环,因为黄浦江的泄流与吴淞口潮位密切相关,而且吴淞口上游沿江各断面潮位也由吴淞口潮位推算而得.吴淞口潮位站处于长江口和黄浦江口,除了天文潮外还受长江和黄浦江径流量的影响,但相对于天文潮而言,径流量的影响很微弱.通过计算结果与实测数据比较分析,采用的相关途径方法具有较高的模拟预报精度,可以用于预报沿江各断面潮位过程.该方法已在太湖流域洪水预报调度系统中得到了应用.
[1]严以新,刘均卫,吴德安,等.长江口综合整治工程前后潮汐特征分析[J].河海大学学报:自然科学版,2009,37(1):100-104.(YAN Yi-xin,LIU Jun-wei,WU De-an,et al.Analysis of tidal characteristics before and after construction of regulation projects in Yangtze River estuary[J].Journal of Hohai University:Natural Sciences,2009,37(1):100-104.(in Chinese))
[2]赵人俊.水文预报文集[M].北京:水利电力出版社,1994.
[3]李国芳,谭亚,张秀菊.感潮河段上游流量对潮位预报的影响[J].河海大学学报:自然科学版,2006,34(2):144-147.(LI Guo-fang,TAN Ya,ZHANG Xiu-ju.Influence of upstream discharge in tidal level prediction for tidal reaches[J].Journal of Hohai University:Natural Sciences,2006,34(2):144-147.(in Chinese))
[4]方国洪,郑文振,陈宗镛,等.潮汐和潮流的分析和预报[M].北京:海洋出版社,1986.
[5]方国洪.潮汐分析和预报的准调和分潮方法:Ⅰ.准调和分潮[J].海洋科学集刊,1974,9:1-15.(FANG Guo-hong.Quasiharmonic constituent method for analysis and prediction of tides:Ⅰ.quasi-harmonic constituent[J].Studia Marina Sinica,1974,9:1-15.(in Chinese))
[6]方国洪.潮汐分析和预报的准调和分潮方法:Ⅱ.短期观测的分析[J].海洋科学集刊,1976,11:33-56.(FANG Guo-hong.Quasi-harmonic constituent method for analysis and prediction of tides:Ⅱ.analysis of short-term observationt[J].Studia Marina Sinica,1976,11:33-56.(in Chinese))
[7]方国洪.潮汐分析和预报的准调和分潮方法:Ⅲ.潮流和潮汐分析的一个实际计算过程[J].海洋科学集刊,1981,18:19-39.(FANG Guo-hong.Quasi-harmonic constituent method for analysis and prediction of tides:Ⅲ.a calculational method of tidal current and tide analysis[J].Studia Marina Sinica,1981,18:19-39.(in Chinese))
[8]王骥,方国洪.不完整逐时潮汐观测记录的分析[J].海洋学报:中文版,1981(2):193-210.(WANG Ji,FANG Guo-hong.An analysis of incomplete hourly tidal records[J].Acta Oceanologica Sinica,1981(2):193-210.(in Chinese))
[9]陈宗镛.潮汐学[M].北京:科学出版社,1980.
[10]王莹辉,谭亚.近17年福建沿海台风及风暴增水特性统计分析[J].河海大学学报:自然科学版,2008,36(3):384-389.(WANG Ying-hui,TAN Ya.Characteristic analysis of the typhoons and storm surgesin the Fujian coastal area over the past 17 years[J].Journal of Hohai University:Natural Sciences,2008,36(3):384-389.(in Chinese))
[11]SMITH L H,CHEN R T.Tidal and tidally averged circulation characteristics of Suisun Bay,Califorlia[J].Water Resources Research,1987,23(1):143-155.
[12]AMIN M.The fine resolution of tidal harmonics[J].Geophysical Journal of the Royal Astronomical Society,1976(2):293-310.
