载荷不对称卧式容器的应力计算

李若兰,丁 杰,聂莉莹

(武汉新世界制冷工业有限公司,湖北武汉430023)

1 概述

制冷机组结构紧凑性、制冷剂进出接管布置等需求,常常使得机组中卧式容器的支座不能实现对称设置。此时卧式容器的载荷不对称,不对称载荷作用下容器支座反力不相等;容器上的弯矩分布不对称,容器的跨中截面不再是可能发生失效的危险截面,因此,不能直接运用JB/T4731提供的方法进行卧式容器的设计计算。

本文通过对支座非对称设置的卧式容器进行载荷分析,建立弯矩方程,分析弯矩方程,给出工程适用的计算方法:卧式容器支座反力的计算;弯矩极值位置的计算,以及极值弯矩的计算。计算得到的结果用于计算JB/T4731中相应应力的计算。

确定弯矩的极值位置尤为重要,结构布置时,可以避免在弯矩极值处开孔,降低容器运行使用的风险。

2 载荷分析

2.1 容器的载荷[1]

采用Zick在实验研究基础上提出的近似分析和计算方法,将卧式容器简化成承受均布载荷、支撑在两个铰支点上的简支外伸梁。在载荷的作用下,容器受到的外力为:两端作用一对力偶M;竖直剪力V;容器本身、物料、附件的总重量沿着圆筒长度方向均匀分布的均布载荷q;均布载荷q作用产生的支座反力FⅠ和FⅡ。如图1(a)所示。

其中[2]:

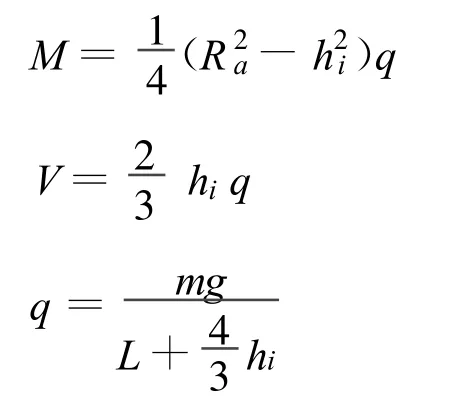
各符号的意义同JB/T4731-2005《钢制卧式容器》。

2.2 载荷作用下容器的支座反力

用截面法求出支座Ⅰ处的支座反力FⅠ:

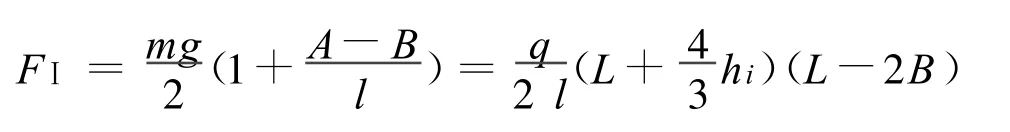
支座Ⅱ处的支座反力FⅡ:

3 剪力与弯矩[3～5]

容器在外部载荷作用下,截面上存在剪力和弯矩,不同截面上的剪力弯矩通常不同,需要了解它们的变化和最大位置,因此,选取如图1(a)所示坐标系 (悬臂长的一侧处于左侧,并以容器的左端为坐标原点),用坐标x表示容器截面的位置,运用材料力学的分析方法将剪力、弯矩表示成坐标x的函数。

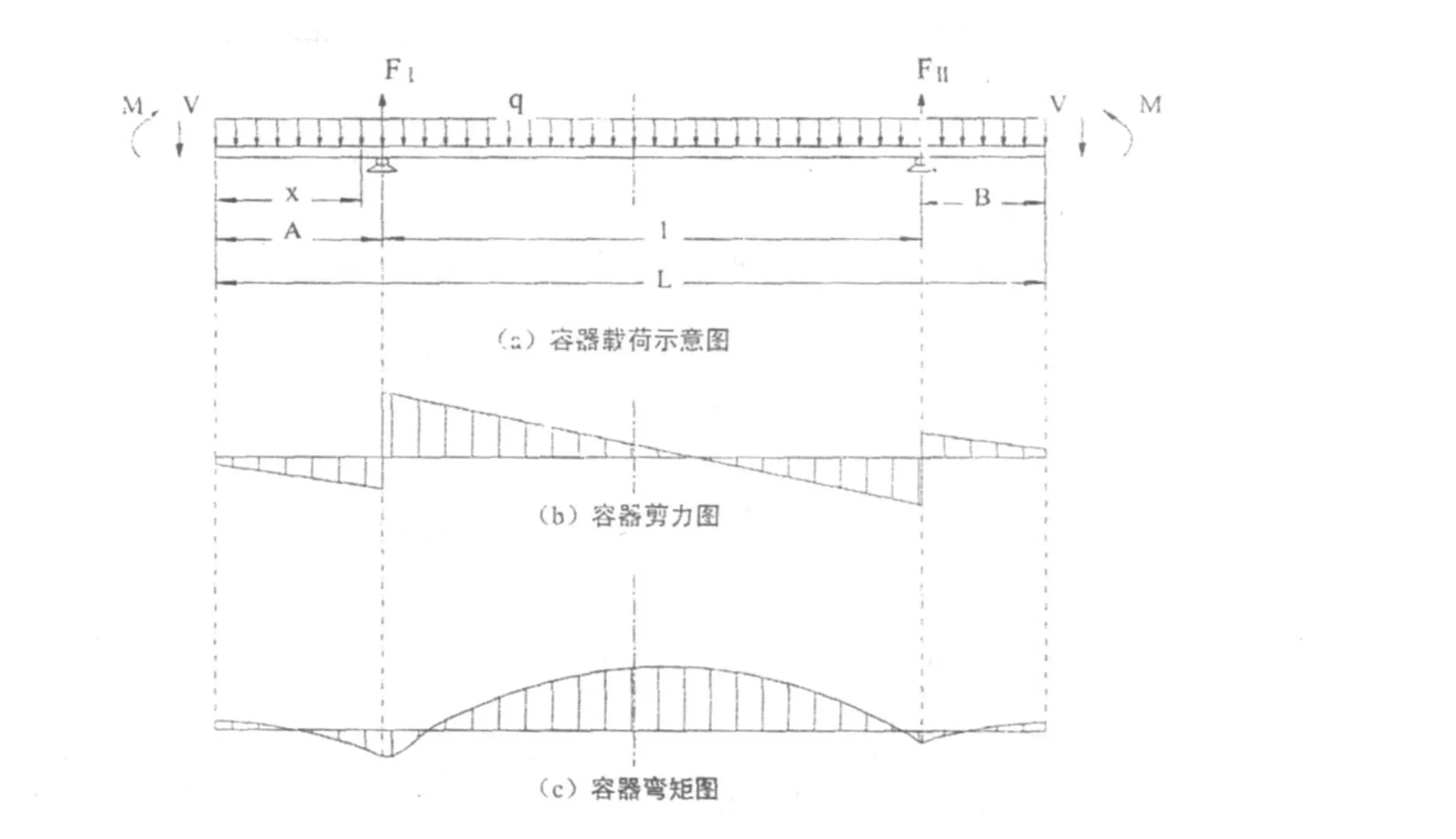
图1 容器的载荷、剪力图、弯矩图

3.1 剪力方程

容器A段、l段、B段上的剪力变化需要用不同的方程来表示(以下各式符号见图1(a))。容器A段剪力方程:

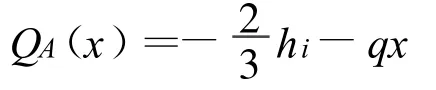
容器l段剪力方程:

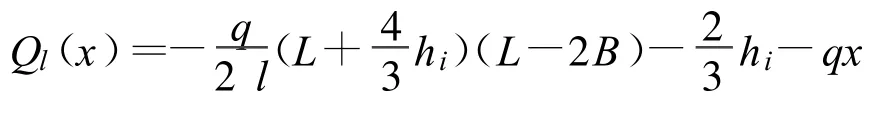
容器B段剪力方程:

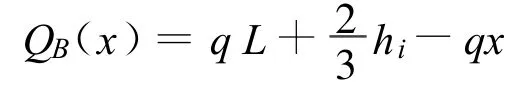
3.2 弯矩方程

容器的A段、l段、B段上的弯矩方程,也应分段考虑。各段上的弯矩方程,可以由力偶M单独作用产生的弯矩方程;竖直剪力V单独作用产生的弯矩方程;均布载荷单独作用产生的弯矩方程;支座反力单独作用产生的弯矩方程叠加。

容器A段上的弯矩方程:

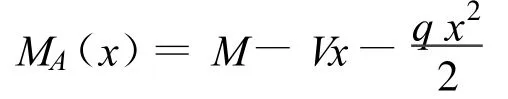
容器l段上的弯矩方程:

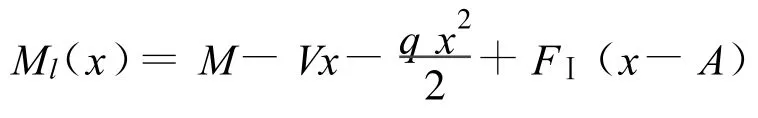
容器B段上的弯矩方程:

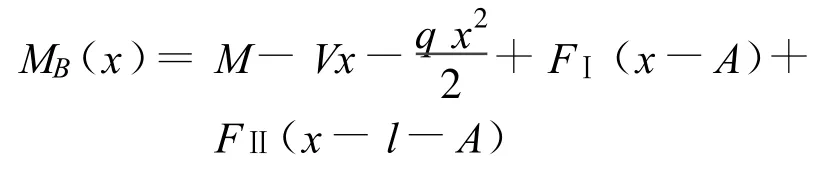
4 方程分析

根据剪力、弯矩方程做出剪力图、弯矩图可以更形象表示剪力、弯矩沿容器轴线方向的变化,各载荷作用下容器的剪力见图1(b),各载荷作用下容器的弯矩见图1(c)。

4.1 剪力方程分析

剪力方程表明各段的剪力图是一条斜直线,最大剪力出现在方程的端点处。经过分析计算可以得到最大剪力出现在容器支座处的筒体截面上。实际应用时,将容器各段的端点坐标代入相关方程计算可得到该方程所表示容器段的最大剪力。

4.2 弯矩方程分析

4.2.1 对A段弯矩方程求导得:

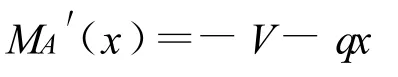
在 [0,A] 上,MA′(x)＜0。因此,MA(x)由MA(x)=M开始单调下降,当X=A时 (支座 Ⅰ所处的截面上),弯矩达到最大值,其值为:

4.2.2 对l段弯矩方程求导得:

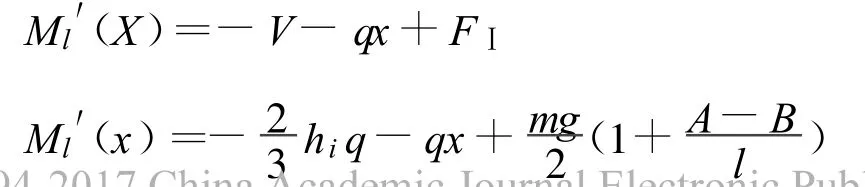
其驻点 (导数等于0的点)为:

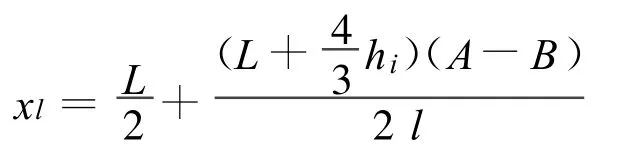
支座不对称设置时,驻点不在容器的跨中截面上,即容器的弯矩极值位置不在容器的中间截面上,当A＞B时,极值位置远离A(悬臂长侧),靠近B(悬臂短侧),反之,当A＜B时,极值位置远离B,靠近A。极值位置靠近悬臂短的一侧。

在驻点处弯矩有极值,此极值为:

4.2.3 对B段弯矩方程求导得:

在 [l+A,l+A+B] 上,MB′(x)＞0。因此,MB单调增加,由X=l+A处 (支座 Ⅱ所处的截面上)的MB(L+A)单调增加到MB(L)=M。弯矩最大值出现在支座 Ⅱ所处的截面上,其值为:

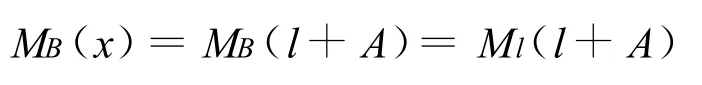
5 结果分析

卧式容器的支座设置不对称时,两个支座的反力不同,支座 Ⅰ处的反力大于支座 Ⅱ处;弯矩分布不对称,支座 Ⅰ处的弯矩大于支座 Ⅱ处的弯矩,弯矩的极值不在容器的跨中截面上;出现的规律在弯矩方程分析中已描述。容器的最大弯矩可能出现在极值处,也可能出现在支座 Ⅰ截面上。按图1所示坐标系,相关的计算式如下:

5.1 支座反力计算

支座 Ⅰ处的反力:

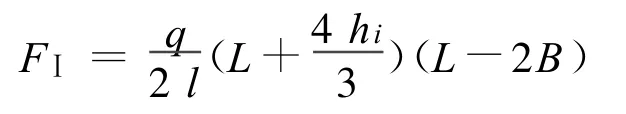
支座 Ⅱ处的反力:

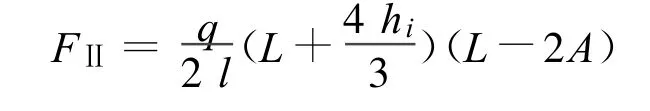
FⅠ＞FⅡ。实际运用时,计算FⅠ即可。

5.2 最大剪力计算

一般情况下,支座 Ⅰ处最大剪力在支座的右侧筒体截面上:

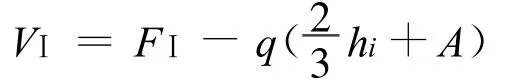
支座 Ⅱ处最大剪力在支座的左侧筒体截面上:

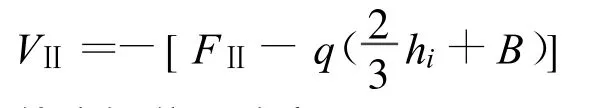
5.3 极值弯矩位置确定

容器l段上弯矩方程的驻点处是最大轴向弯矩产生的位置,因此,只要对容器两支座之间的驻点进行计算,就能确定最大轴向弯矩产生的位置。驻点位置的计算按下式:

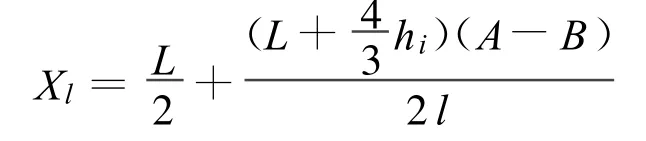
5.4 极值弯矩计算

极值处的弯矩根据下式计算:

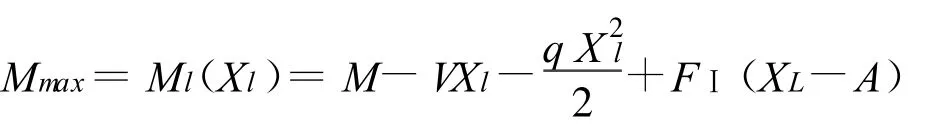
5.5 支座 Ⅰ平面上的轴向弯矩

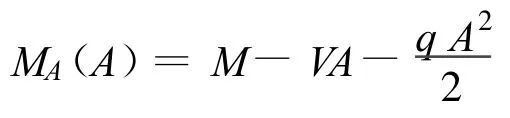
6 结果运用

以上各式的结果,可以用于计算JB/T4731《钢制卧式容器》中相应的应力。

6.1 支座的反力FⅠ

代替JB/T4731中的F,用于计算圆筒切向剪应力r、封头切向剪应力rh;圆筒周向应力 σ5、σ6、σ6′、σ7、σ8;鞍座腹板水平分力Fs;鞍座压缩应力σsa。

6.2 极值弯矩Mmax

用于计算JB/T4731中极值截面上圆筒最高点处的应力σ1和圆筒最低点处的应力 σ2。

6.3 支座 Ⅰ平面上的轴向弯矩MA(A)

用于计算JB/T4731中支座截面上圆筒的轴向应力σ3,支座截面最低点处的轴向应力 σ4。

压力试验工况下的计算过程和上述过程一致,只需要将以上计算式中的均布载荷q用试验工况下的均布载荷q′代替。

[1] 李世玉.压力容器设计工程师培训教程[M].北京:新华出版社,2005:398-410

[2] JB/T4731-2005,钢制卧式容器[S].

[3] 机械设计手册[M].北京:化学工业出版社,1985:96-98

[4] 许本安等.材料力学[M].上海:上海交通大学出版社,1988:140-161

[5] 工程力学课件梁的弯曲 [EB/OL].http://www.hetaodaxue.com:8080/.../.