不确定度分析方法在暖通空调实验中的应用

2011-06-19李书明

制冷 2011年1期

李书明

(广州大学,广州510006)

1 引言

随着能源形势日益紧张,人民日益关注建筑和暖通空调节能,而其中的工作如政府决策的数据数据确定、建筑和设备效能测评标识、相关技术研发领域、室内环境测评、用户冷热计量、能源测评审计与计量等都离不开实验分析来选择测量方法以及分析测量值的可靠性。而不确定度分析作为实验分析和实验结果处理的重要手段,也受到重视。

国际上早在1980[1]就已开始研究用不确定度(uncertainty)来表示实验结果,更自1993年[2,3]大力推广采用测量不确定度的概念。我国的测量行业标准JJF1059-1999[4,5]即是对GUM1995[3]的等同采用,对科学研究、工程技术及商贸中大量存在的数据的处理和表示均具有适用性。测量不确定度的定义[3～5]是:与测量结果相关联的一个参数,用以表征合理地赋予被测量之值的分散性。不确定度指导致测量结果偏离的程度,用分散性尺度来评价测量结果质量,综合了全部误差因素对实验结果的影响。

而我国当前虽然也逐步的重视不确定度分析,如建筑节能检测标准JGJ/T132-2009和JGJ/T177-2009均有涉及,但却一直用误差理论而非不确定度分析来指导暖通空调实验[6]。

而误差为测量值偏离真值的程度,以标准差来评价测量结果的质量,反应的是测量误差对实验结果的影响。若用误差理论来表示被测量的值,即使对完全已知或猜测的误差因素进行补偿、修正后,所得结果依然只能是被测量的一个估计值。另外,误差理论通常只考虑实验数据处理阶段的误差或不确定度,而对实验规划及设计阶段的误差及不确定度分析没有考虑或不够重视。然而正是实验规划及设计阶段的不确定分析才能从根本上控制实验的方案精确度和减少系统不确定度,因此需要推广不确定度分析。

不确定度分析是优化实验的强大工具,可应用于实验分析的所有阶段 (见表1),尤其是实验的规划和设计阶段。根据待测对象确定实验方案和测量方法,选择适当的测量仪器,搭建试验台,实施实验,经过 “实验—修改—再实验”,正确得出并报告实验结果。

表1 实验不确定度分析

2 不确定度分析方法

根据要求不同,不确定度按有标准不确定度、合成不确定度、扩展不确定度三种表述方式。根据估计方法不同,其分为按统计分布估计的A类不确定度和按非统计分布估计的B类不确定度两类。

2.1 A类标准不确定度

1)在相同测量条件下,对同一被测量进行连续多次测量的复制性条件下,采用贝塞尔公式计算得到:样本均值即测量结果,样本标准差即测量结果的标准不确定度。

2)如果被测量随时间随机变化,即为随机过程,则应采用较差法 (阿伦方差法)求标准不确定度。

例如测定f实验,且f=y(τ)。对被测量进行m+1次测量,每次测量取样时间为τ,共有m个较差 [yi+1(τ)-yi(τ)];阿仑方差:则f的A 类标准不确定度:

3)当被测量X的估计值是由实验数据用最小二乘法拟合的一条曲线上得到,则标准不确定度可由拟合函数和不确定度传递率确定。

如对Y=mX+c来说:

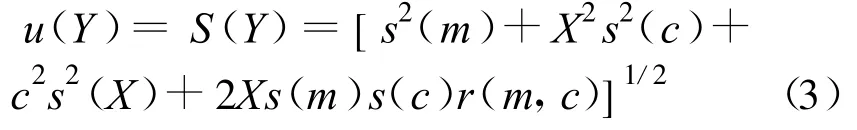
式中,s(m),s(c),s(X)分别为m,c,X的估计标准差;r(m,c)为m和c的相关系数。

2.2 B类标准不确定度

标准不确定度u(f)可用X的有关信息或资料来评定。信息来源可以是:以前测量的数据;经验和对有关仪器性能或材料的资料;厂家技术说明书;鉴定证书、校准证书、测试报告或其他提供数据的文件等。

评定方法为:一般根据经验或有关信息和资料,分析判断被测量的可能值的区间(-α,α),并假设测量误差的概率分布,则不确定度为:u(x)=α/k,式中 α为区间的半宽度,k为包含因子,由要求的置信水平估计。

2.3 合成不确定度

当测量结果为其他被测量求得时,按各被测量的方差和协方差来计算合成不确定度uc(y)。在实际工作中,当被测量接近高斯正态分布时,可采用测量结果y及其合成不确定度uc(y)表示,即Y=y±uc(y)

此式是基于y=f(x1,x2,…,xn)的泰勒级数的一阶近似,称为 “不确定度传播率”。偏导数Ci=∂f/∂xi是在Xi=xi时评定的,称为灵敏系数。式中:x,x是X,X的估计值,且u(x,x)=u(x,xi)是xi,xj的协方差的估计值。u(xi)可以由A类或B类得到;

协方差与相关系数r(xi,xj)的关系是:r的绝对值大于0.7时,一般称为强相关,否则为弱相关。当在估计输入量之值xi时,如果使用了同一个测量标准、测量仪器、参考数据或甚至具有相当大不确定度的测量方法即会产生明显相关,就必须考虑其相关性。

2.4 扩展不确定度

扩展不确定度用U表示,指确定结果区间的量,被测量可望大部含于此区间。U由合成不确定度uc(y)乘包含因子k得到。

由于用合成不确定度表示测量结果仅有P=68%的置信概率,所以一般采用扩展不确定度来表示测量结果,即Y=y±U。

求扩展不确定度方法:

1)取扩展不确定度U=kuc,一般取置信概率为95%的包含因子k95=2,有时取置信概率为99%的k99=2.6(大样本近似计算值,JJF1059取3);在多数的检定/校准结果中,其合成标准不确定度均可用第一种简单的方法进行计算。

2)如果uc(y)的自由度较小,并要求区间具有规定的置信水平时,取U=kPuc。式中k与P由各影响分量自由度Vi及合成标准不确定度的有效自由度Veff来确定。A类评定时,通常对每个Xi测量ni次,自由度为vi=ni-1;如果有n个数据点用最小二乘法拟合成曲线来估计m个参数,则每个参数的标准不确定度自由度为n-m。B类评定时,由相对标准不确定度 (由经验定)带入式确定。而当Veff足够大时,两法相同。

3 实验用不确定度分析

3.1 总体不确定度分析

通过不确定度分析,实验人员可以从规划及设计阶段综合考虑系统精度、经济性或简便性等实验的各个方面,即在达到实验结果要求的精度下减少资源消耗;通常有不同的实验方法或多种实验方案,对于每一种方法,有不同的不确定度传递特性,需确定哪一种方法的测量结果最接近真值,并分析所用方法中哪个量的测量是最重要的。如对同一物理量的测量,应根据研究对象,列出各种可能的实验方法,分析各种方法的适用条件,比较各种方法的局限性与可能达到的实验精确度 (或不确定度)等因素,并考虑方案实施的可能性,最后选出最佳的实验方法。

若不确定度传递方程如:

则实验结果的不确定度表述为:

式中UMFi为不确定度放大系数 (正态敏感系数),表征变量对结果不确定度的影响;UPCi为不确定度贡献百分比,包含有UMFi和变量i的不确定度量级的效果,因此在实验设备和方法选择完成后,便可估计出测量不确定度。

3.2 详细不确定度分析

在进行详细不确定度分析时,根据误差源分别评定每个测量量的系统和随机不确定度,然后再合成为整体不确定度。若测量方程为式(5),则系统不确定度和随机不确定可以按下式(TSM方法)计算:

式中bX,sX为X变量的系统不确定度和随机不确定度,分别指每两个有相同系统误差源变量的协方差和每两个有相同随机误差源变量的协方差。而随机不确定度相关项的协方差一般为0。

在稳态测试中,如果式 (5)中为单变量测量且有足够多的样本数,可采用贝塞尔公式计算随机不确定度:

显然,直接法考虑了各被测量之间的相关性,有着可能更精确的结果。但直接法需要通过多次测量获得足够的数据信息,测量的时间长度也是很重要的,所以在单次测量中一般不应使用直接法。

在实验的调试阶段,可用不确定度分析来发现实验设备、操作运行、测试方法等方面的问题并加以改进。用1阶复制水平进行运行逐步检查,使用N阶扩展不确定度评估对接受的结果和理论值的结果进行比较,如果在结果中随机不确定度比预期值大得多,则表明某些随机误差源被低估了,需继续调试。

在试验的实施阶段,可用不确定度分析来进行测试点的校正。1)校正测点范围:因为高阶回归方程需要较多的测点,尽量选用适当的坐标系 (如对数坐标系)和尽量低阶的关系式,可减少必要的测点数量。2)设定测试序列:一般情况下,随机地分布测试点得到的测试结果更接近实际情况,因此我们设定测试点是随机的而不是连续的。

3.3 实验结果处理

通过回归分析获得数学表达式的方法大量应用于实验数据处理上。实验数据回归方程Y=mX+c中Y、m、c的回归标准差:

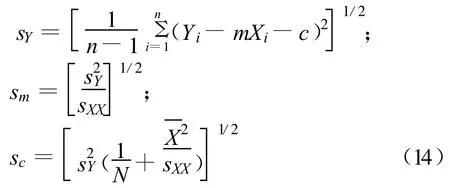
当不考虑X的随机不确定度时,sY可近似为回归随机不确定度,可用来衡量所有随机因素对Y影响的大小,sY愈小,回归精度愈高。但sY仅仅表达了拟合曲线的随机不确定度,并不包含参考标准、数据获取、试验台搭建、概念模型引起的不确定度中的任何一项。

4 应用举例

4.1 整体不确定度分析例子

为了测定某圆管外壁对流换热系数,分析两种实验方案:

1)稳态方法:

根据能量守恒W=h(πDL)(T-Tα)得到:

式中电功率W、圆管外径D、长度L和圆柱外壁温T、来流温度Tα均通过测量获得;

2)非稳态方法:

式中圆柱体的质量M、直径D和长度L,测试时间τ,圆柱比热c通过测量或查资料获得。

(1)试验中,忽略辐射和热传导的影响,h和c为常数,忽略圆柱内部热阻,即温度均匀分布。若温度是单独测量的,应用不确定度传递方程(15)有:

表2 两种方法各式中测量值的不确定度表

(2)用A类或B类方法评定各测量量的不确定度 (表2),并将数值带入 (15～16)式得到 (17～18)式:

图1 稳态测试图 (左);非稳态测试图 (右上);对比图 (右下)

(3)结果分析

稳态测试总体不确定度分析:由相对不确定度传递公式看出,对结果不确定度影响,△T最大,而D相对于△T的来说可以忽略,W的影响在W值大时较小,即对总体不确定度影响较小,相反影响较大;从测试线图可以看出,在h较大时,不同温差条件下的测试均可满足总体不确定度的要求,这是因为h较大时,W=0.2426亦较大,W相对不确定度较小。同样原因,在h较小时,W为影响总体不确定度的关键因素,只有在低于0.5W的情况下才能得到h总体不确定度5%的结果。

非稳态测试总体不确定度分析:由相对不确定度传递公式看出,对结果不确定度影响,c较大,可以通过改善c值来改进实验;由线图可以看出,随着h值的增大,τ逐渐成为总体不确定度的决定性因素。并在大h值的领域,要获得5%的h总体不确定度,需要τ为7ms,8ms或更少时间。

对比分析:从不确定度传递方程线图可以看出,稳态测试h的总体不确定度随着h的增大而减小,非稳态测试h的总体不确定度随着h的增大而增大;在h＜150时,宜采用非稳态测试;在h＞200时,宜采用稳态测试;而在150＜h＜200时,两者基本相当 [h单位为W/(m2℃)]。

4.2 详细不确定度分析例子

对某煤样品的热值测量数据进行处理。其测量数学方程为:

H=式中H为热值 (W/g);(T2-T1)为燃后温升 (℃);C热量计热当量(W/℃);e为燃烧放热量 (W);M为样本质量。此处是一个样本对样本实验。

4.2.1 0阶复制水平分析

表3 0阶水平变量不确定度估计表

系统不确定度:

随机不确定度 (由上公式计算H=18981W/g):

即sH=199 W/g;

合成不确定度:

4.2.2 1阶复制水平分析

对同一样本进行了26次测量,并求出样本均值=18578W/g和用贝塞尔公式计算出标准差SH=364.6W/g,但可以看出该随机不确定度较0阶水平算出的199W/g大,这是应为1阶计算结果考虑了样本对样本实验中测量系统和材料组分的效果。

因样本变化的随机不确定度为:

上式结果说明,因为煤组分的变化而引起的随机不确定度,实际上比测量系统的随机不确定度还要大。在样本对样本试验中,可以利用0阶复制水平随机不确定度和多次测量1阶随机不确定度后,来确定样本变化对结果不确定度的影响。

4.2.3 N阶复制水平分析

在N阶复制水平下,使用0阶水平计算的系统不确定度和1阶直接测量的随机不确定度来计算合成不确定度和扩展不确定度 (95%置信概率)。

得到置信概率为95%的测量结果:18758±180W/g;或18800W/g,1%相对不确定度。

5 结论

在暖通空调实验测量领域,包括建筑能耗检测、建筑设备测评、暖通实验室测量等众多领域的实验规划、实验设计、实验报告等领域应推广应用不确定度分析,以在满足试验要求的情况下节省资源和加大试验的可操作性。

不确定度分析理论是误差理论的进一步发展,主要按不确定度来源分为系统不确定度和随机不确定度,系统不确定度可以根据经验、资料、仪器说明书评定,而随机不确定度可以根据直接测量样本标准差来获得。

在实验规划阶段,可以通过初算不确定度,校核初选实验方案是否满足实验要求的精度,以选定实验方案;另外可以根据TSM法不确定度传递方程进行分析,计算敏感系数等可观值来找到对实验结果起关键影响的因素,改进实验,选择实验设备,优化实验方案。在试验实施阶段,可以通过监测实验不确定度,监测实验设备的运行情况,以达到优良的运行效果。在试验报告阶段,以方便报告不确定度的形式组织线图和回归方程形式,并按标准要求给出测试线图和回顾方程各部分的不确定度。

[1] BIP M.Recommendation INC-1.CIPM 81-11,1981

[2] The 1993 ISO Guide to the Expression of Uncertainty?in Measurement(GUM)

[3] The 1995 ISO Guide to the Expression of Uncertainty?in Measurement(GUM)

[4] 中国国家计量技术规范——通用计量术语和定义JJF1001-1998[S]

[5] 中国国家计量技术规范——测量不确定度评价与表示JJF1059-1999[S]

[6] 李峰,姬长发.建筑环境与设备工程实验及测试技术[M].北京:机械工业出版社,2008,9

[7] The 2005 standard ASME PTC19.1 Test Uncertainty

[8] The 2008 JCGM Supplement 1 to the GUM:Evaluation of Measurement Data—Propagation of Distributions Using a Monte Carlo Method

[9] Coleman H W,Steele W G,Experimentation,Validation,and Uncertainty Analysisfor Engineers.New York:John Wiley&Sons,2009

[10] 刘智敏.不确定度原理[M].北京:中国计量出版社,1993,6

[11] 宋明顺.测量不确定度评定与数据处理[M].北京:中国计量出版社,2000,1

[12] 叶培德.测量不确定度[M].北京:国防工业出版社,1996,5