基于上游渐扩管安装条件的内锥流量计性能预测

李彦梅，徐 英，张朝龙，郭 玉，唐 飞

（1.安庆师范学院物理与电气工程学院，安徽 安庆 246001；2.天津大学电气与自动化工程学院，天津 300072）

基于上游渐扩管安装条件的内锥流量计性能预测

李彦梅1，2，徐 英2，张朝龙1，郭 玉1，唐 飞1

（1.安庆师范学院物理与电气工程学院，安徽 安庆 246001；2.天津大学电气与自动化工程学院，天津 300072）

针对內锥流量计使用灵活性要求，利用计算流体动力学数值仿真和实流实验相结合的方法，研究上游渐扩管安装条件对内锥流量计性能的影响，以获取所需的最短直管段长度。研究对象是100mm口径、β值分别为0.45，0.65，0.85三种结构类型的样机。开展了基线和渐扩管两种类型的实验，仿真和实验的介质均为常温水，雷诺数范围分别为0.2488×105～2.488×105和0.3843×105～2.479×105，仿真结果和实验结论一致。利用附加不确定度和流出系数相对误差作为主要的评价标准，给出了上游渐扩管安装条件内锥流量计所需的直管段长度。

渐扩管；内锥流量计；计算流体动力学；流出系数；雷诺数

0 引 言

内锥流量计在许多方面表现出比传统节流式流量计更为出色的性能［1］，但内锥流量计尚未标准化，对其安装条件的研究成了国内外讨论与关心的热点。Stephen A.Ifft［2］等人利用实验方法先后研究了上游单个90°弯头与不在同一平面的、前后紧接的双90°弯头以及全开和半开阀门对内锥流量计关键参数的影响；此后，S.N.Singh［3］，R.J.W.Peters［4－5］先后对内锥流量计的抗流场扰动性能开展了实验研究；李彦梅［6－7］等人利用数值仿真和实流实验相结合的方法研究了上游单弯头和双弯头安装条件对内锥流量计性能的影响。天津大学的流量实验室先后对内锥量计流出系数、可膨胀系数及湿气测量等方面展开了研究，并取得了宝贵的经验成果［8－10］。

近年来，国内虽然掀起了推广应用内锥流量计的热潮，但对内锥流量计的关键技术指标、安装条件未进行相应的标定，大多直接沿用美国McC.公司的产品说明书。针对100mm口径、β值分别为0.45，0.65，0.85的内锥流量计，开展了在渐扩管安装条件下基线及上游不同直管段长度的仿真研究，并做了一定的实验验证，预测了上游渐扩管安装条件下的内锥流量计所需的最短直管段长度。

1 建模与研究方案设计

1.1 内锥流量计的几何结构

内锥流量计的结构如图1所示。内锥体可以看作是两个底面积相同的圆台拼接而成，通过支架固定并与管道同轴，上游直接在管壁取压，下游采用锥尾取压方式，锥尾的压力通过锥体内导压孔和支架中的测量管传递到管壁取压孔。

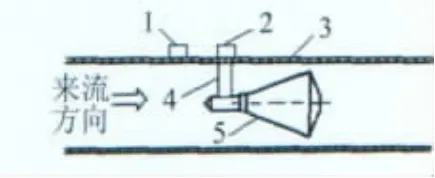
图1 內锥流量计几何结构Fig.1 Structure of V－cone flowmeter

1.2 研究方案设计

对100mm 口径、β值分别对0.45，0.65，0.85的内锥流量计开展在上游渐扩管安装条件下的数值仿真，然后针对β值为0.65的内锥流量计进行实流测试，管内径100mm定义为1D。为保证管内流体流动为充分发展的湍流状态，物理实验样机上游直管段100D，仿真实验样机上游直管段10D。其中，渐扩管安装条件为：DN50的圆型管道经过渐扩管（长200mm）与DN100的圆型管道相连。设计方案如表1。

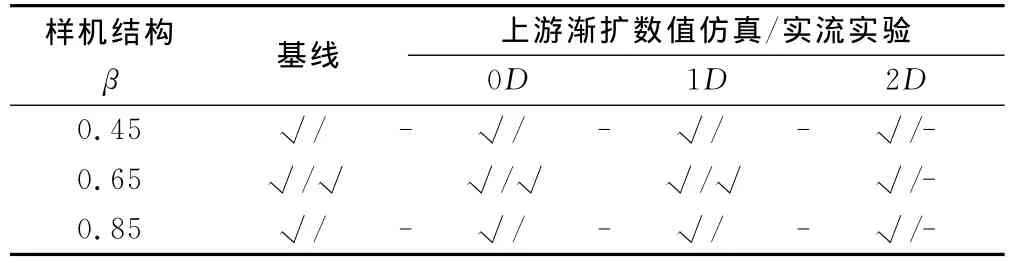
表1 研究方案设计（研究介质：常温水）Table 1 Research project design（medium：water with ambient temperature）

2 数值仿真

2.1 几何模型与网格剖分

仿真几何模型利用Gambit2.2.30软件建立，采用三维方式建模以保证数值仿真几何模型与物理实验样机完全一样。流量计主体管段长400mm，在渐扩管的前端设有10D直管段，流量计后方直管段长10D。为更准确地获得锥体附近压力的变化情况，在网格剖分时，采用size函数，对锥体附近的网格进行细密的划分，而远离锥体的上、下游直管段区域网格逐渐变得稀疏，网格类型为四面体，网格单元数量约60万。三维几何模型与网格剖分如图2所示。

将网格文件导入FLUENT 6.3.26软件后，为优化网格结构，减少网格数量，提高计算效率，首先将网格类型转换成六面体，然后利用分离式求解器进行求解，仿真介质为常温水。入口条件为速度入口和流出出口；流速为0.5～5m／s；并采用标准壁面函数法对近壁区进行处理，壁面为无滑移条件。

图2 内锥流量计三维模型及网格剖分（局部）Fig.2 Three－dimensional model and grid cutting of V－cone flowmeter（partial）

2.2 湍流模型与边界条件

对比目前常见的湍流模型，标准k－ε模型在科学研究及工程领域获得了最广泛的检验与成功应用［11］，但当应用于强旋流、弯曲壁面流动或弯曲流线流动时，会产生一定的失真。杨胜等［12］在对汽车外部流场仿真研究中，比较了Spalart－Allmaras一方程模型、标准k－ε模型、RNG k－ε模型、Realizable k－ε模型和RSM模型的预测结果后，认为RNG k－ε模型的预测性能要强于其余的4种模型。因此研究中采用RNG k－ε模型计算流场，利用有限体积法实现控制方程的离散化，采用SIMPLE算法进行求解。根据GAN等的研究［13］，在仿真时，除压力项采用二阶迎风格式外，其余都利用了Quick格式进行离散。亚松弛因子采用FLUENT软件的默认值，实践证明其收敛效果比较好，残差收敛精度设为10－5。计算时选取5个流速点，方向取入口面的法线方向。其中100mm口径内锥流量计仿真湍流参数如表2所示。

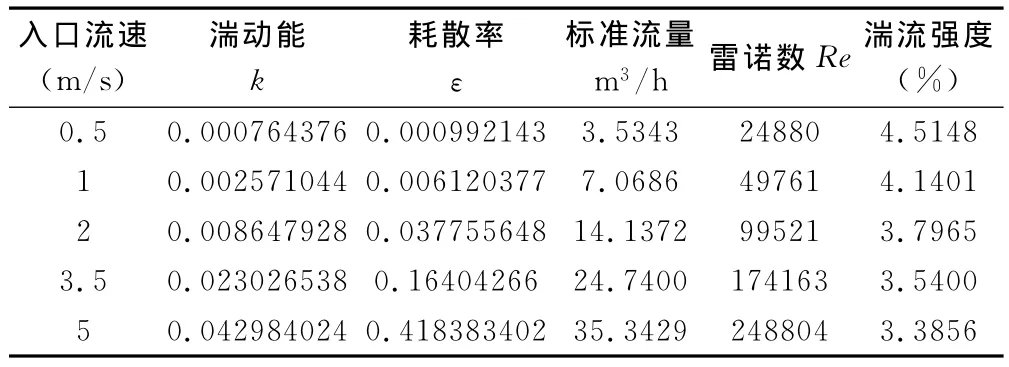
表2 100mm口径内锥流量计仿真湍流参数Table 2 Turbulence parameters of simulation with 100mm diameter V－Cone flowmeter

湍流参数计算如下：

（1）湍动能k求解

式中，uavg为平均速度；I为湍流强度。

湍流强度依据经验公式进行计算

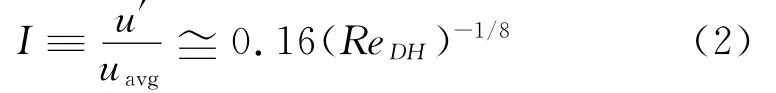
式中，uavg为脉动速度的均方根；ReDH为以管径为特征尺度计算的雷诺数。

（2）湍流耗散率ε的求解

式中，Cμ为湍流模型中指定的经验常数，一般取0.09；而l为湍流长度尺度，与管道内径L的关系为l＝0.07L。

2.3 计算结果

流出系数C是内锥流量计的关键参数之一，对于不可压缩流体，流出系数C定义为內锥流量计中实际流量与理论流量的比值。根据能量守恒定律和质量守恒定律，可以推导出C的计算公式为

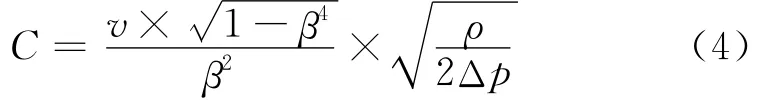
式中v是流动稳定的情况下内锥流量计上游管段（即100mm口径管道）中流体的流速（m／s）；Δp 为上下游取压点测得的压差值（Pa）。该公式使用伯努利方程进行推导，由于流动中会有能量损失，压力的测量结果也并非为一个平面上的平均压力，并且在实际内锥流量计中，存在低压取压L形立柱的影响，因此，流出系统C往往小于1。

通过点表面积分法，对数值仿真计算结果进行后处理，计算锥体上下游的压力差，并根据公式（4）计算出流出系数。图3即为3种β值在上游渐扩管安装条件下流出系数与雷诺数的关系曲线。

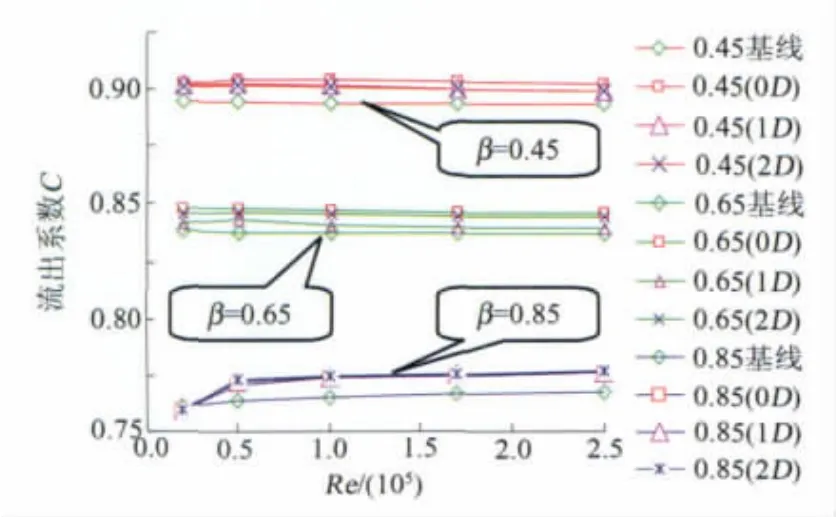
图3 C－Re曲线Fig.3 C－Re curve

从图3可见：（1）流出系数与β值有关，且β值越大，流出系数越小；（2）在渐扩管安装条件下，对于相同的流速，随着前直管段长度的增加，其C－Re曲线越接近基线数据；（3）渐扩管对流出系数的影响程度与β值有关，其中β值为0.85时影响最强，而β值为0.65时，流出系数变化最小，说明β＝0.65的流出系数较稳定，受扩管影响程度较弱。

2.4 压力场分析

以β＝0.45，入口流速v＝0.2m／s为例，提取锥体上游和下游局部压力场云图，分析上游不同直管段长度对上、下游压差的影响。压力场云图如图4～6所示。

图4 上游渐扩0D压力场云图（β＝0.45）Fig.4 Pressure field nephogram of upstream 0Dexpander（β＝0.45）

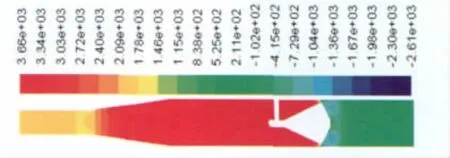
图5 上游渐扩1 D压力场云图（β＝0.45）Fig.5 Pressure field nephogram of upstream 1Dexpander（β＝0.45）

图6 上游渐扩2 D压力场云图（β＝0.45）Fig.6 Pressure field nephogram of upstream 2Dexpander（β＝0.45）

由压力场云图可见：（1）流体流经锥体时，其上、下游的压力发生了变化，上游压力大于下游压力；（2）在渐扩管的作用下，渐扩管段的压力变化最为明显，上游压力降低，经渐扩管压力又逐渐升高；（3）随着锥体上游直管段长度的增加，渐扩管上游低压区的长度逐渐减小。

2.5 数值仿真与实流实验的比较

根据仿真预测结果，针对β＝0.65的内锥流量计，展开了在渐扩管安装条件下的实流实验研究。实验在天津大学流量实验室完成，实验时根据实验装置的现有能力尽可能拓展了雷诺数范围。图7为＝0.65数值仿真与实流实验的C－Re曲线。

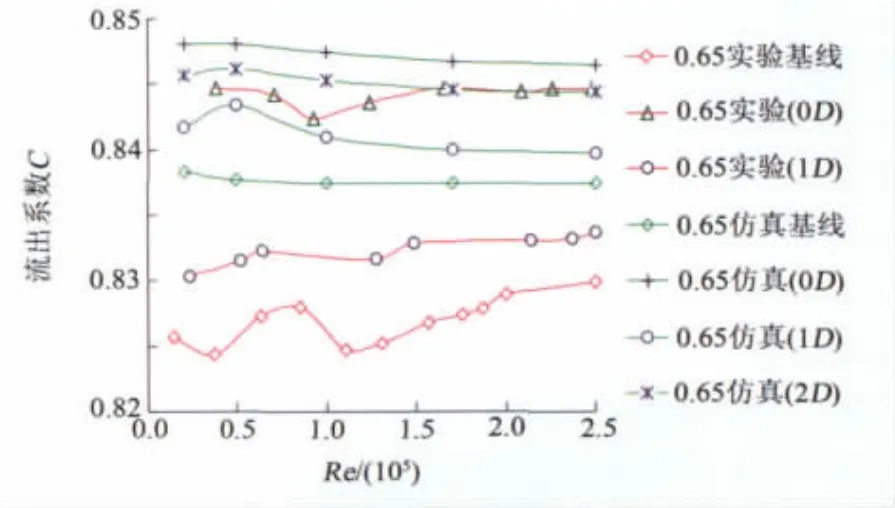
图7 仿真／实验C－Re曲线（β＝0.65）Fig.7 C－Re graph of simulation／experiment（β＝0.65）

由图中可见：（1）在渐扩管安装条件下，流出系数与雷诺数的变化规律与基线一致；（2）在内锥流量计前加0D、1D和2D直管段，其数值仿真结果中，流出系数相对于基线测试流出系数的偏差在±0.6%～±0.9% （＜±1%）；而实流试验中，在0D直管段长度下，流出系数相对与基线测试流出系数的偏差大于1%，在1D 直管段长度下，其偏差为0.7%（＜±1%）。

2.6 误差来源分析

（1）湍流模型输运各向异性导致预测精度存在差异，另外，在锥体尾部流动出现分离，产生一个较大的旋涡区，而锥体尾部的取压口恰好位于旋涡区中。因此，对旋涡区的计算精度，会直接影响差压值计算的准确度，而差压值与流出系数值直接相关。

（2）本实验中采用RNG k－ε模型，该模型虽修正了湍动黏度，并在ε方程中增加了一项，从而反映了主流的时均应变率，但RNG k－ε模型仍是针对充分发展的湍流是有效的，即是高Re数的湍流计算模型，而在渐扩安装条件下，雷诺数较小，从而限制了预测精度。

3 评价方法与建议的直管段长度

通常将附加不确定度Δσ和平均流出系数相对误差δ-c作为安装条件的主要评价标准。当Δσ与δ-c均小于0.5%时，认为渐扩管安装条件对内锥流量计的影响可忽略，直管段长度适当；当δ-c≥1%或Δσ和δ-c均大于0.5%时，直管段长度不适当；当Δσ、δ-c两者之一远小于0.5%，另一值在0.5%～1%之间，此时直管段长度需谨慎使用。

根据以上评价方法，仿真预测结果表明：β值为0.45，0.65时的上游渐扩管直管段长度为1D；对于0.85的内锥上游渐扩管直管段长度最少为2D。

本研究中，通过仿真预测并对β值为0.65的内锥流量计进行了实验验证，实验根据天津大学流量实验室水流量实验装置的现有能力，尽可能拓展了雷诺数的范围。本研究结果与美国McC.公司给出的结果进行了对比，如表3。

对比分析如下：（1）实验介质不同。McC.为气体和液体两种；本实验为一种介质，即常温水。（2）雷诺数范围不同。McC.液相的范围上限2×105，无下限；本实验雷诺数在0.3843×105～2.479×105之间，仿真雷诺数范围在0.2488×105～2.488×105之间。（3）下游直管段不同。McC.给出了两种情况，即1D／2D；本研究仅限于对上游渐扩管影响研究，将下游直管段长度固定为3D。（4）上游直管段长度不同。McC.认为如果雷诺数范围相同，对于同一范围内的节流比，上游直管段完全相同，分别为1D／2D；在仿真／实验研究的雷诺数范围内，节流比为0.45，0.65时，所需直管段长度为1D，当节流比为0.85时，所需直管段长度最小为2D。

表3 仿真／实验研究结果与美国McC.公司数据的比较Table 3 Data comparison with simulation／experimention and American McC.

4 结 论

开展了基线实验和上游渐扩实验两类研究，涉及3种节流比，仿真和实验一共进行了15组。将平均流出系数相对误差与附加不确定度作为上游渐扩管对内锥流量计性能影响的主要评价指标。仿真预测结果和实验结果吻合，并与国外相关实验数据进行了对比，给出了不同的研究结论。在本研究雷诺数范围内，研究得出了β值为0.45，0.65所需直管段长度为1D，而β值为0.85所需直管段长度最小为2D的结论。

［1］孙延祚.“V”型内锥式流量计［J］.天然气工业，2004，24（3）：105－110.

［2］IFFT S A，MIKKELSEN E D.Pipe elbow effects on the V－cone flowmeter［C］.ASME Fluids Engineering Conference，Washington D.C.，1993.

［3］SINGH S N，SESHADRI V，SINGH R K，et al.Effect of upstream flow disturbances on the performance characteristics of a V－cone flowmeter［J］.Flow Measurement and Instrumentation，2006，17：291－297.

［4］PETERS R J W，STEVEN R，CALDWELL S，et al.Testing the wafer V－cone flowmeters in accordance with API 5.7“Testing Protocol for Differential Pressure Flow Measurement Devices”in the CEESI Colorado test facility［J］.Flow Measurement and Instrumentation，2006，17：247－254.

［5］PETERS R J W.Testing the wafer v－cone flowmeters in accordance with api 22.2“testing protocol for differential pressure flow measurement devices”［R］.2006.

［6］李彦梅等.上游单弯头对内锥流量计性能影响的仿真与实验研究［J］.仪器仪表 学报，2009，30（6）：1195－1201.

［7］李彦梅等.上游弯头对内锥流量计性能的影响的仿真与实验研究 ［J］.实验流体力学，2010，24（1）：84－88.

［8］于中伟.内锥流量计的仿真与实验研究［D］.天津：天津大学，2005.

［9］吴经纬.内锥流量计可膨胀系数与湿气测量特性的数值研究［D］.天津：天津大学，2007.

［10］杨会峰.内锥流量计可膨胀系数与湿气测量特性的实验研究［D］.天津：天津大学，2007.

［11］王福军.计算流体动力学分析——CFD软件原理与应用［M］.北京：清华大学出版社，2004.

［12］杨 胜等.汽车外部复杂流场计算的湍流模型比较［J］.汽车工程，2003，25（4）：322－325.

［13］GAN G，RIFFAT S B.K－factors for HVAC ducts－numerical and experimental determination［J］.Building Services Engineering Research and Technology，1995，16（3）：133－139.

李彦梅（1973－），女，河南省南阳市人，副教授，硕士。主要研究方向为流体流动参数检测、智能化仪表。通信地址：安徽省安庆市菱湖南路128号（246011）。联系电 话：15155484331；E－mail：lym7301＠163.com。

Prediction of the performance of cone flowmeters installed with an upstream expander

LI Yan－mei1，2，XU Ying2，ZHANG Chao－long1，GUO Yu1，TANG Fei1
（1.School of Physical ＆Electrical Engineering，Anqing Teachers College，Anqing Anhui 246001；2.School of Electrical ＆Automatic Engineering，Tianjin University，Tianjin 300072，China）

Based on numerical simulation and actual－flow experiment，the influence of the installation of upstream expander on cone flowmeter is investigated to obtain the minimum length of straight pipe within flexibility requirements.The objects of study are three types of prototype with 100mm diameter andβvalues of 0.45，0.65，0.85.The medium of simulation and experiment is water with ambient temperature，and the Reynolds are 0.2488×105～2.488×105and 0.3843×105～2.479×105respectively.Two types of experiments are carried out，namely，the baseline and expander experiments.Evaluated in terms of additional uncertainty and the relative error of discharge coefficient，the required length of straight pipe of cone flowmeter is given after the installation of an upstream expander.

expander；V－cone flowmeter；computational flow dynamics；discharge coefficient；Reynolds number

TP212.1

A

1672－9897（2011）04－0055－05

2010－12－01；

2011－02－10

国家“863”计划资助项目 （2007AA04Z180）；安徽省高校省级自然科学重点项目（KJ2010A235）；2009年度安庆市重点科技项目（20091002）