含双馈风电机组的配电网潮流分析
2011-06-13孙银锋李国庆顾黎明
孙银锋,李国庆,顾黎明,韩 悦
(1.东北电力大学 电气工程学院,吉林 吉林132012;2.浙江省台州电业局,浙江台州317000)
靠近负荷中心的分布式发电系统对配电网有着多方面影响。鉴于分布式电源在电力系统中所占比例的不断扩大,研究分布式发电对系统稳态运行的影响势在必行。近年来,作为一种清洁的可再生能源,风力发电日益受到重视。上世纪80年代以来,风力发电机制造水平不断提高,单机容量不断增大,风力发电机控制系统日趋完善,对风力发电并网技术的研究也逐渐深入。本文将通过潮流计算,针对靠近负荷中心的风力发电系统对放射状链式配电网络影响进行探讨。
含风机的配电网潮流计算可以用来评估风机并网后对系统的影响,配电网的规划以及配电网的网络重构、故障处理、无功优化和状态估计等都需要用到配电网潮流数据。同时,它也是分析分布式发电对电网稳定性的影响等其他理论研究工作的基础[1]。
在风力发电中,由于风速变幻莫测,所以对风能的利用存在一定的困难。因此改善风力发电技术,提高风力发电机组的效率,最充分地利用风能资源,有着十分重要的意义。本文将采用双馈电机,来解决风力机转速不可调、机组效率低等问题。另外,由于双馈电机对无功功率、有功功率均可调,对电网可起到稳压、稳频的作用,提高发电质量[2]。
本文将双馈风电机组按一定方式接入典型配电系统,通过改进牛顿法进行潮流计算,进而分析风机的不同接入点对系统的影响。
1 风速模型及双馈风电机组
1.1 风速概率分布曲线
风速分布曲线是风能资源计算的基础。风具有随机性很大的性质,能够反映风的统计特点的重要形式是风速的概率分布曲线。在判断一个地方的风况时,需要通过足够多和足够长时间的气象资料,以获取各种风速出现的频率。风速分布一般为正偏态分布,用于拟合风速分布特性的线型很多,如:瑞利分布、威布尔分布、对数正态和耿贝分布等,而其中威布尔(Weibull)单峰双参数分布曲线,被普遍认为是适用于风速统计特性的概率密度函数。
风速的威布尔概率密度函数可表示为:
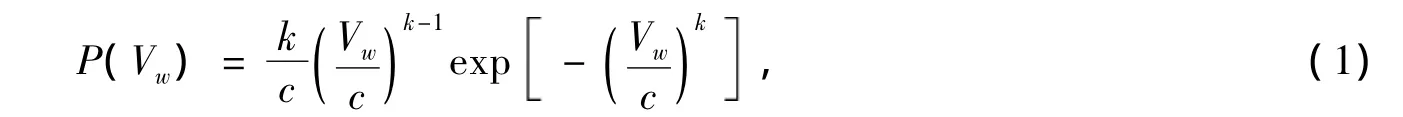
式中,Vw是风速,c和k为威布尔分布的尺度参数和形状参数。c反映的是平均风速的大小;k对应着威布尔分布的形状,取值范围一般为1.8-2.3之间,k=2时,又称为瑞利(Rayleigh)分布,很多地区的风速分布可以采用瑞利分布,k=3.5时,威布尔分布已很接近正态分布。
风力机感受到的风速是轮毅高度H处的风速,在风速数据处理和分析过程中要对测风高度H0处的风速Vwo进行修正,修正公式为:

式中α为高度修正系数,通常在0.1-0.4范围内。
用于计算风速分布参数的方法有多种,如最小误差逼近法、均值与方差估算法、极大似然法等。通过这些方法计算威布尔分布的尺度参数c和形状参数k,这样,风速的分布形式便确定了,还可以计算出能直接体现风能资源状况的风能特征指标,进而就可以通过风力机组的输出功率与风速之间近似关系得到输出功率的随机分布。
1.2 风电机组输出功率模型
风电机组的输出功率与风速的关系曲线称为风电机组功率特性曲线,风力发电机输出功率主要取决于风轮机轮毂高度处的风速,可以用分段函数表示:

图1 风电机组输出功率特性曲线

风电机组功率特性曲线,见图1。
若将图中a,b改为直线,则分段函数变为如下形式
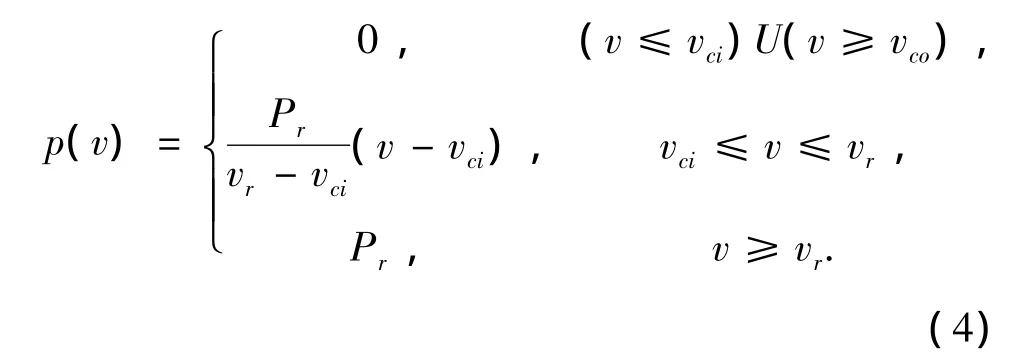
1.3 双馈感应式风力发电机组
双馈感应式风力发电机组以其变流器容量小,有功和无功功率可独立解耦控制的特点,随着技术的成熟,现已成为目前变速恒频风力发电机组的主流机型。变桨距双馈风力发电机组是一种采用脉宽调制技术的风力发电机组,是目前风力发电分析与控制的研究重点之一,其结构如图2。

图2 双馈感应式风力发电机
这种发电机除定子绕组与电网有电气连接外,其转子绕组也通过变频器与电网相联。通过在转子绕组中施加变频电流,在定子绕组中感应出恒频电势,从而实现了风力发电机组的变速恒频运行。变频器的容量取决于发电机变速运行时的最大滑差功率,一般仅为发电机额定容量的1/4~1/3。变速恒频双馈风电机组能控制发电机的滑差在恰当的数值范围内变动,因此可优化风力机叶片的桨距调节,减少风力机叶片桨距的调节次数。由于风力机变速运行,其运行速度能够在一个较宽的范围内调节,使风力机达到最优功率系数,从而提高发电机组的效率。
2 配电网潮流计算
2.1 配网潮流特点及算法
配电网络具有许多不同于高压输电网的特征,例如:环网设计,开环运行,正常运行时是辐射型树状;支路参数r/x的比值较大;三相支路参数不对称和三相负荷不平衡问题比较突出等。因而也就对配电网的潮流计算方法提出了特殊的要求。回路阻抗潮流算法以及其改进算法的特点是较好的收敛性,处理网孔能力较强,通过适当的编号技术,可减少存储需求和提高计算速度。但该方法占用较多的内存,处理时间较长。相应的改进算法则解决了存储和运算时间问题。前推回推法(Backward/forward Sweep Algorithm)在配电网络的潮流计算中应用也较广泛。当用来进行辐射状配电网的潮流计算时,该算法的效率是所有算法中最高的,占用内存也很少,但当应用于环状网络时则需要进行特殊的处理,当网络中含有PV节点时也需要进行特殊的处理,这在一定程度上限制了此方法的应用。
本文将采用改进牛顿法进行配网潮流计算。传统牛顿法潮流算法的实质是逐次线性化,求解过程的核心是反复形成并求解修正方程。此方法对于辐射型配电网从理论上来讲是收敛的,但在具有运算量大的缺点。而改进牛顿算法可化简原雅可比矩阵,从而有效降低计算量。
2.2 改进牛顿法原理
在传统的牛顿法中,潮流问题可以化成如下形式:

改进牛顿法生成一个UDUT形式的近似雅可比阵,在此基础上线性化潮流方程,进行前推回推可求得系统状态变量的增量。该法对传统牛顿法的雅可比阵进行了简化,简化之前要针对配电网的特点做一些假设
(1)首先,配电网中的线路长度都不长,并且线路上的功率都不高,因此可以假设相邻两条母线的电压近似相等。(2)配电网是放射形网络,网络中没有环路,则

其中,DB和DG均为对角矩阵,DB=ViVjBijcosθij,DG=ViVjGijcosθij。DB中对角线位置上的第k个元素DBk对应于第k条支路,该支路的源母线为母线i,目标母线为母线j,是个p×p矩阵,p是线路k的相数(1≤p≤3)。DG与DB相似。An-1为母线对支路的关联矩阵。可以将修正方程写为:

将上式写成复数矩阵的形式如下:
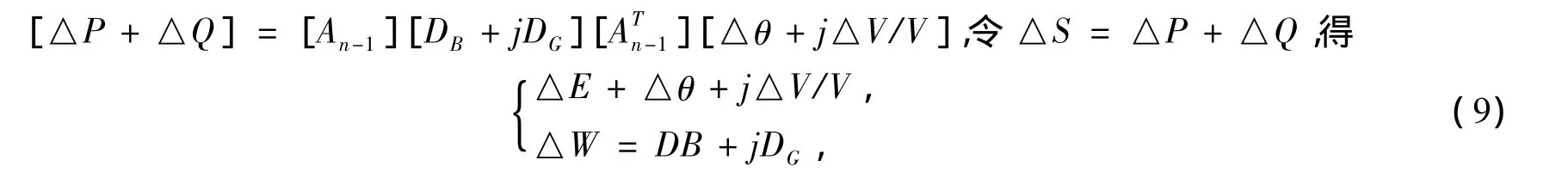
可将上式改写为如下迭代形式:

式(12)为前代过程,式(11)为回代过程。
3 仿 真
本文采用图3所示的IEEE33节点配电系统进行分析。本文将双馈风力发电机组节点设为PV节点;33节点默认与电网相连,仿真计算中视为平衡节点;基准功率取为100 MVA,电压等级为12.66 kV,计算精度为0.00001。下面将对风机的不同接入地点进行潮流仿真,进而分析风机的接入对此配电系统运行的影响。
首先,根据前面介绍的风速模型模拟出风速曲线,见图4,进而得到风力发电机的有功功率曲线,见图5。
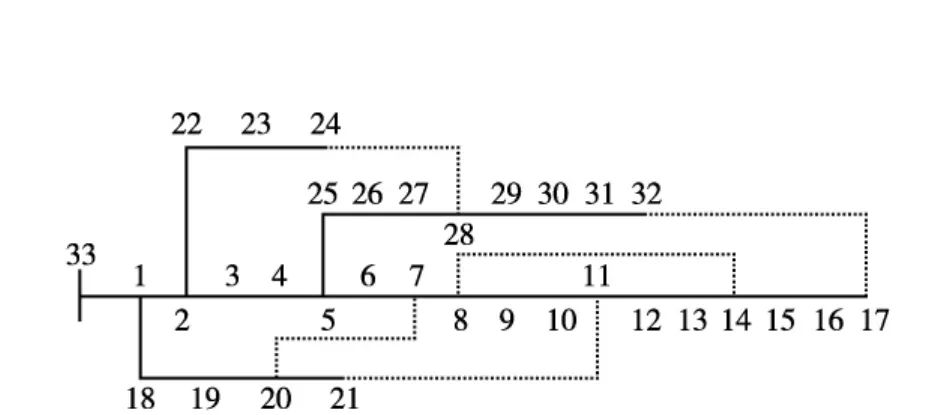
图3 IEEE 33节点配电系统

潮流计算结果表明,不同的风电机组接入位置对潮流的收敛情况影响不大,如图6所示,潮流基本在四次迭代后收敛,得出潮流仿真数据。
3.1 风机接入位置对系统网损的影响
下面来看双馈风力发电机组的不同接入位置对系统网损的影响。从表1中可以看出,在同一条配电馈线上,风电机组的接入越靠近电网则网损越大,如节点1,节点18,有时往往带来比未加风机时大很多的网络损耗。相反,越是远离电网侧的接入点,越能控制网损在理想的范围内,如接入点分别为节点21,32,17时,有时甚至会比未加入风机时网损更小,如从节点11或节点7接入。当然,这只是定性的分析,而不能单纯根据距离远近来定量的分析网损情况,因为系统的馈线连接方式不同,负荷变化和分布都将会对结果产生影响。

图6 潮流收敛曲线

表1 风机接入点对网损的影响
3.2 风电机组接入对负荷节点电压的影响
表2为未计及风力发电机时,在恒定负荷下的部分母线电压情况,而图7和图8分别模拟常规异步风力发电机和本文引入的双馈感应风力发电机接入节点24后,各个节点电压情况。显然,风力发电机的接入,使得配电网中母线电压受到一定影响,即当风速较高或者风速波动剧烈时,会使母线电压降低,这是由于,随着风速的提高风电机组会从系统吸收更多的无功功率,使部分母线电压,尤其是距离风电场电气距离较近的电压水平有所下降。
另一方面,观察图7和图8可以发现。双馈风力发电机与常规异步风力发电机相比,并不会改善电压的水平,然而却可以显著的改善由于风力发电的随机性,间歇性所导致节点电压波动,提高电能质量。

表2 风机接入前各母线电压

4 结 论
本文首先分析了风速模型以及风电机组功率输出模型,并介绍了变桨距双馈风力发电机组的特点以及其控制方式。在仿真计算中,将双溃风电机组按一定方式接入典型配电系统,并在潮流结算中将其视为PV节点。通过对仿真结果的分析可知,不同的接入位置对潮流的收敛情况影响不大,却对网损有一定影响,大体上随接入点距离电网侧的距离增大而有减小趋势,理论的推广尚需深入研究。双馈风机电源接入配电网,相对于常规异步风力发电机对馈线的电压分布的改善作用明显,即可有效平复风力发电的随机性,间歇性所导致节点电压波动,以满足用户对电能质量的要求。
[1]王守相,江兴月,王成山.含风力发电机组的配电网潮流计算[J].电网技术,2006,30(21):42-45.
[2]雷亚洲.与风电并网相关的研究课题[J].电力系统自动化,2003,27(8):84-89.
[3]刘威,赵渊,周家启,等.计及风电场的发输配电系统可靠性评估[J].电网技术,2008,32(13):69-74.
[4]丁明,吴义纯,张立军.风电场风速概率分布参数计算方法的研究[J].中国电机工程学报,2005,25(10):107-110.
[5]Y Zhu,K.Tomsovic.Adaptive Power Flow Method for Distribution Systems with Dispersed Generation[J].IEEE Transactions on Power Delivery,2002,17(3):822 -827.
[6]Fang Zhang,Carol S.Cheng.A Modified Newton Method for Radial Distribution System Fower Flow Analysis[J].IEEE Transactions on Power Systems,1997,12(1):389 -397.
[7]代江,王韶,祝金锋.含分布式电源的弱环配电网络潮流计算[J].电力系统保护与控制,2011,39(10):28-31.
[8]张国新.风力发电并网技术及电能质量控制策略[J].电力自动化设备,2009,29(6):29-33.
[9]李新,彭怡,赵晶晶,等.分布式电源并网的潮流计算[J].电力系统保护与控制,2009,37(17):78-81.
