基于ANSYS的小型重力坝坝形优化分析

王开拓，辛全才，纪新帅

（西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100）

0 引言

重力坝设计满足规范要求最主要、最普遍的核算是沿坝基面抗滑稳定安全系数和上游坝踵拉应力，而这两项受上游坝面线形的影响较大[1]。目前，重力坝断面形式大都采用理论三角形，这可以使断面优选工作充分简化，但它仅能使建基面上的控制条件得到满足，而在位置较高的截面上常有所富余，并且坝体上下游存在折点，容易产生应力集中，所以，三角形断面并非理论上的最优断面。通常设计重力坝时均不考虑地基对坝体的影响，即把地基作为刚性来处理，但实际工程中地基不可能是刚性的，弹性地基及地基变形都对坝体有影响。

基于以上考虑，本文将重力坝上下游坝面做成曲面形状，利用ANSYS平台并采用APDL参数化语言，实现建模、加载求解和优化分析。

1 重力坝优化模型

重力坝基本断面的优化过程应满足3个原则：①坝体的抗滑稳定必须满足规范规定的安全系数；②坝体的应力必须满足规范的要求；③在给定设计参数和施工条件下，大坝基本断面的面积最小或接近最小[2]。

首先把工程实际问题抽象为一个数学规划问题，然后确定结构优化数学模型，最终建立重力坝断面优化数学模型。选取的设计变量为x=[a1、b1、a2]T，a1、b1、a2为坝体断面上下游曲线方程的系数，其中，a1、a2均大于零，b1不小于零。建立的数学模型为

目标函数 minA（x）

约束条件

式中，A（x）为坝体断面面积，m2；H为坝高，m；L3为坝底宽度，m；KS为按抗剪强度计算的抗滑稳定安全系数；∑W为计算截面以上坝体全部荷载的垂直分力总和，向下为正，kN；∑P为作用于坝体上全部荷载沿滑动面方向的分力，kN；U为作用在接触面上的扬压力，kN；f为接触面间的摩擦系数，混凝土与基岩间的f常取0.5～0.8；MW、MPZ、MU分别表示重力、竖直方向上的分力、扬压力对于计算截面形心的力矩，∑M为荷载对该截面形心的力矩总和，逆时针方向为正，kN·m；T为计算截面沿上下游方向的宽度，m；σyu为坝趾垂直应力，MPa；σu为坝踵垂直应力，MPa，且 σu≥0。

2 基于ANSY S重力坝参数化建模

2.1 问题描述

拟定上下游坝面曲线为二次抛物线y=ax2+bx+c的形式，并将系数 a1、b1、a2作为设计变量。初始a1、b1、a2分别为1、0.9、0.5。取坝体参数：弹性模量（E） 为 2.8×107kN/m2，泊松比（μ） 为 0.167，容重（γ）为24 kN/m3；地基参数：E为2.0×107kN/m2，μ为 0.3，γ为26 kN/m3； 水的容重为 9.8 kN/m3，扬压力折减系数（α）为0.2，折减点在坝踵处；坝体与地基面的抗滑摩擦系数（f）为0.6。有限元分析采用平面应力模型，计算基础的选取范围为：坝基上游取1.5倍坝高，下游取2倍坝高，坝基深度取2倍坝高。

2.2 优化分析过程

设上游水位与坝顶齐平，下游无水。拟定的设计变量a1、b1、a2，坝体和坝基的材料参数E、μ、γ均为已知量。进行断面优化设计时，取坝体在上游满库、下游无水情况下的稳定和应力状态为控制条件，并在坝踵处设有防渗帷幕。坝体荷载：坝体自重W（垂直向下）、上游静水压力 Px（水平向右）、Py（垂直向下）和扬压力 U（垂直向上）。计算过程中将这4项荷载同时作用在重力坝模型上（见图1）。以模拟坝体实际受力状况，获得较好地反映实际情况的优化结果，而不是几项荷载作用结果的简单线性叠加[3]。

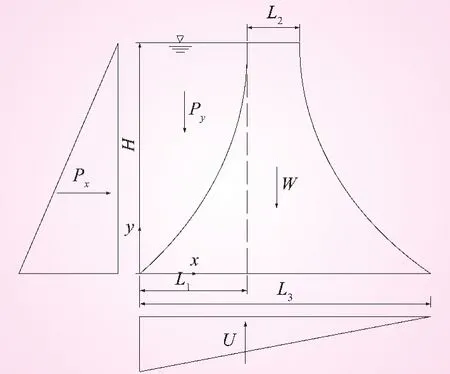
图1 曲线形重力坝荷载示意

对模型依次进行网格划分、施加荷载及位移约束，求解并进行优化分析，进一步确定优化变量。本文以曲线形重力坝参数化模型为基础，假定H为30 m，坝顶宽度（L2）为3 m，f为0.6。首先采用ANSYS自带的零阶方法进行计算，然后将所得数据作为初值，再用一阶优化的方法进行二次计算。

3 优化结果分析

3.1 不同坝形

为了详细地了解曲线坝形的优化程度，本文对传统断面也进行了优化。确定在相同的工况、坝高及摩擦系数的情况下对两种坝形进行比较。结果见图2、3（均为笛卡尔坐标系）和表1。

图2 传统断面Y方向应力云图（当量应力值，单位：MPa）

图3 曲线断面Y方向应力云图（当量应力值，单位：MPa）

从图2、3对比可以看出：①两种坝形坝基面均不存在拉应力，越靠近下游压应力越大，且满足规范要求，符合重力坝的应力状态特点，并且曲线形坝体断面坝踵应力略小于传统形坝体断面的坝踵应力；②比较曲线形坝体与传统形坝体的计算结果。在稳定和应力均满足的基础上，底宽加大反而断面面积减少，说明坝体在位置较高的截面上面积存在富余[4]。

从表1可以看出：①传统断面最优的断面形式是上下游坡比分别为0.000 2和0.6的三角形断面，KS为1.08，L3为21.01 m，坝体断面面积为360.09 m2；②曲线断面最优的断面形式的上下游曲线方程分别为y1=1.33x2+1.608x，y2=0.1x2-4.9x+60.025，KS为 1.13，L3为 24.5 m，坝体断面面积为312.4 m2；③两种坝形坝基面都不存在拉应力，且曲线形断面的KS有所提高，面积有所减小，优化结果较为理想。

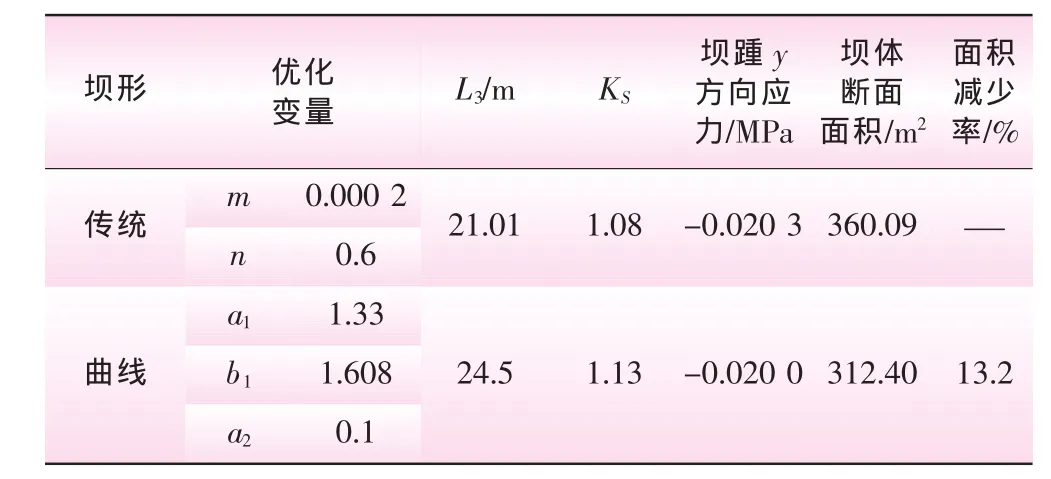
表1 两种坝形优化成果比较

3.2 不同坝高

为了解曲线坝形的适用情况，按照低、中、高坝的划分标准，依次取了30、70、100 m三种坝高进行对比分析。同时对相应的传统断面也进行了分析。优化结果见表2。

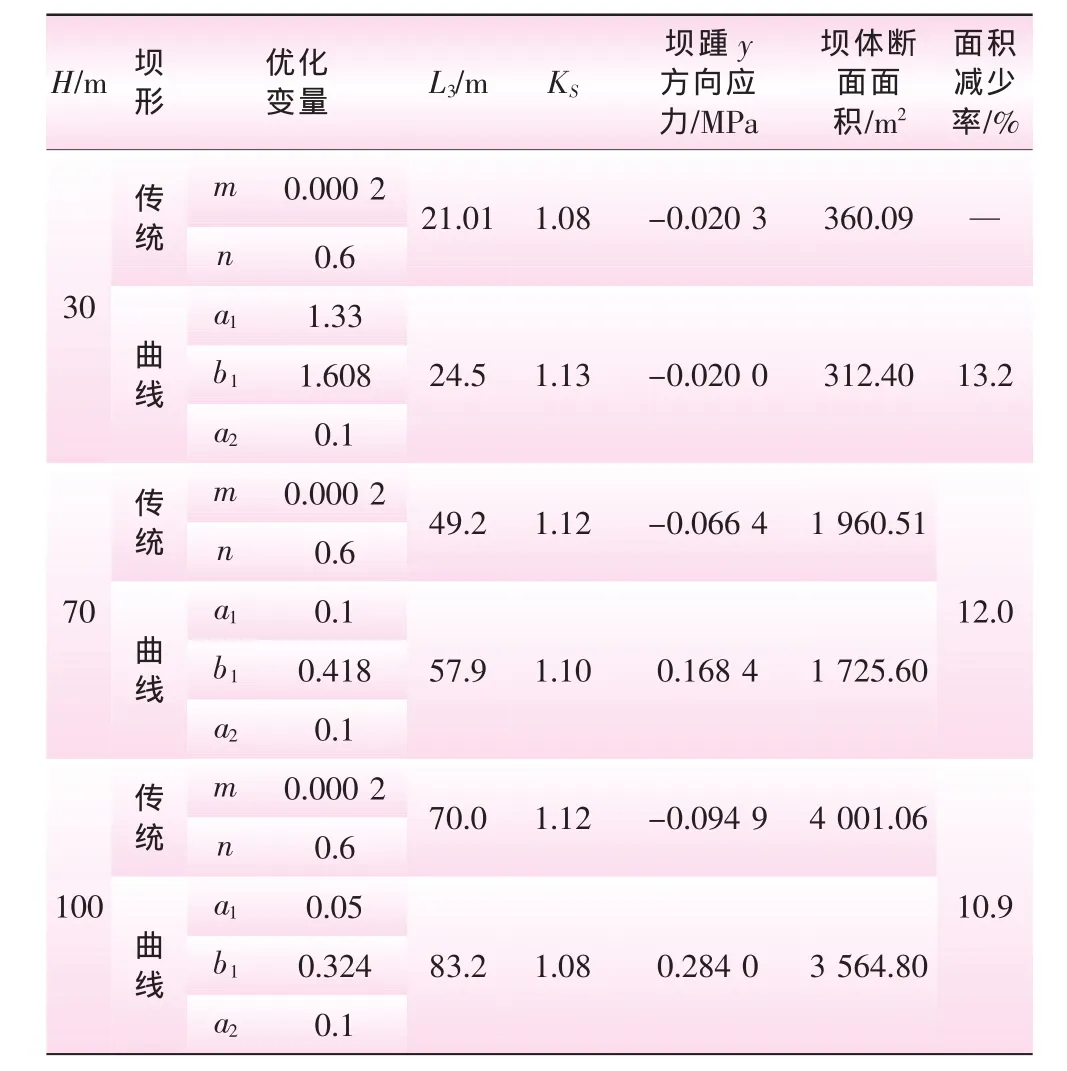
表2 不同坝高优化成果比较

从表2可以看出：①传统断面的优化结果与坝高关系不大，说明传统断面优化不决定于坝高，而决定于外界条件，如地基、筑坝材料、边界条件、荷载等。②从优化结果可以看出参数a1的变化率大于b1、a2，a1对坝形起控制作用。③对于高坝而言，坝基应力对断面形状起控制作用，故随坝高增加，在坝踵开始出现拉应力的同时KS也随之减小。70、100 m曲线形重力坝坝踵y方向拉应力分别为0.168 4、0.284 0 MPa，均不满足规范要求[1]。④重力坝坝踵区是影响大坝安全的关键部位，混凝土重力坝的受力特性接近悬臂梁，坝踵是拉应力区，并存在拉应力集中现象，而混凝土的材料特性是抗压不抗拉，抗拉强度大致只有抗压强度的1/10。因而坝踵区很容易产生裂缝。因而重力坝设计规范不允许坝踵出现拉应力（材料力学法）[1]，但用有限元方法分析，重力坝坝踵出现拉应力是不可避免的[5]。如果出现拉应力则应采取相应的措施，例如设置坝踵块，使拉应力区缩小，拉应力峰值也有所降低。⑤通过对比不同坝高优化结果，曲线重力坝明显优于传统重力坝，面积都有不同程度的减少；但是随着坝高的增加，面积的减少率越来越小，KS也相应有所降低，而且坝基应力不满足规范SL 319—2005要求。

综上所述，可以得出曲线重力坝这种坝形更适合于低坝。

4 结论

（1）将重力坝上下游的坝面改为曲线形式进行尝试，取得了比较理想的结果，说明这种断面形式具有一定的实用价值，值得深入研究。

（2）取30 m坝高的断面作为研究对象，分别采用三角形和曲线形两种不同的断面形式进行优化比较，所得结论为曲线断面面积比传统断面节省13.2%，且KS增大，说明了坝体在位置较高的截面上面积确实存在富余。

（3）通过采取不同坝高进行体形优化设计，比较了不同坝高情况下传统断面与曲线断面的控制条件、坝底宽度、应力分布等。结果发现随着坝高的增加，曲线形重力坝面积减少率越来越小，且在坝踵出现拉应力不符合规范要求的情况。因此可以说曲线重力坝更适合于低坝。

［1］SL 319—2005 混凝土重力坝设计规范［S］.

［2］麦家煊.重力坝基本断面的快速优化设计［J］.水利学报，2000，31（8）:24-26.

［3］祁庆和.水工建筑物（第三版）［M］.北京：中国水利水电出版社，1997.

［4］刘波，李静，翟步凯.曲线重力坝形体的优化设计［J］.水利与建筑工程学报，2006，7（2）:86-87.

［5］厉易生，杨波，张国新.消除混凝土坝坝踵拉应力集中的一种结构措施——设置坝踵块［J］.水力发电，2008，34（6）:59-61.