基于直方图调整的抗几何攻击图像水印
2011-06-12吴康吕灵娟杨胜利孙锐
吴康 吕灵娟 杨胜利 孙锐
合肥工业大学计算机与信息学院 安徽 230009
0 引言
数字水印的鲁棒性是数字水印技术的一个重要指标,其中抗几何攻击的鲁棒性是近年来数字水印领域研究的热点,它要求对图像进行常见的几何变换(如、平移、缩放、旋转等)攻击后,仍能可靠地提取出水印。目前数字水印技术已经得到了很快的发展,出现了一些能够抵抗一定程度几何攻击的水印算法,这些算法可以分为三类:第一类算法是采用具有RST(Rotation, scaling, translation)不变性的变换,如Fourier-Mellin变换,来实现水印的嵌入,这类算法能够较有效地抵抗RST攻击,但却无法抵抗裁剪、纵横比改变等其他攻击;第二类算法是寻找对几何攻击不敏感的特征,把水印嵌入到该特征空间,这类算法抗几何攻击的能力较弱;第三类算法是对受几何攻击后的含水印图像根据一定的方法估计出其所受的几何变形类型和参数,然后进行其逆变换再提取水印。总的来说,现有抗几何攻击的水印算法都能不同程度地抵抗一些几何攻击,但是其中大多数水印算法抗几何攻击的能力比较有限,只能抵抗一定程度内的几何攻击,并且其所能嵌入的水印信息量一般都比较小。
本文提出的基于直方图调整的抗几何攻击数字水印算法是将水印信息通过调整参数后,再将水印信息嵌入在图像的灰度值中,从而使水印的嵌入和提取过程简单、快速、有效,而且其所能嵌入的水印信息量大,抗几何攻击的鲁棒性较强。
1 算法思想
图像灰度直方图是图像的一个重要的全局统计特征。图像像素的统计特征与图像各灰度级的像素个数有关,而与像素在图像中的空间位置无关。首先,当图像遭受几何变换时,其尺寸大小和像素在图像中的空间位置可能会发生很大变化,但由于图像视觉约束机制的存在,图像各灰度级像素的统计特征将保持一定的稳定性,灰度直方图的形状将变换不大。其次,图像颜色直方图相对于幅度不大的平移和缩放以及以观察轴为轴心的旋转等几何变换是不敏感的,对于图像质量的变化也不甚敏感。鉴于以上两点,我们运用图像灰度直方图设计算法以应对水印图像可能遭受的几何攻击,这也正是本文的创新点所在。图1分别给出了Lena图像在RST攻击下图像直方图形状的稳定性。

图1 RST攻击下图像直方图的稳定性
2 算法实现
2.1 嵌入算法
(1)将原始灰度图像记作I= {I(x,y) | 0 ≤I(x,y) ≤ 28- 1,1 ≤x≤M,1 ≤y≤N},将 长 度 为L的二值水 印 序 列 记 作W= {W(i)|W(i) ∈ { 0 ,1},1 ≤i≤L}。为提高水印的安全性,消除水印比特的空间相关性,将水印W进行混沌置乱处理,置乱后的水印记作Ws={Ws(i)|Ws(i) ∈ { 0 ,1},1 ≤i≤L},并将置乱密钥Key妥善保管。
(2)我们根据图像的均值A来确定一个灰度区间,然后仅对灰度属于该区间内的像素统计直方图。该灰度区间为:

其中L为水印序列的长度。然后从整幅图像中找出灰度值属于范围B的所有像素,将灰度范围B平均划分成L个灰度级(即L个“收集箱”)来统计这些像素的直方图H,则每个灰度级包含两个灰度标量,也即一个“收集箱”的宽度为λ=2,每个“收集箱”可以嵌入1bit的水印信息。从而可知直方图H共有L个灰度级,且第i个灰度级所包含的灰度值范围为:

对于图像中任意一像素I(x,y),其位于的灰度级i可以通过下式获得:

(3)下面以嵌入1bit水印信息详细说明水印嵌入策略:
针对其中任意一个“收集箱”,将bin_1和bin_2分别记作该“收集箱”中前后两个灰度值,并将其中的像素个数分别记为a和b,执行嵌入规则如下:

其中,T是设置参数,用来控制需要调整的像素的数量,其取值应该合理折中水印鲁棒性与不可感知性之间的矛盾。通过调整像素值来嵌入水印信息,调整方法如图2所示。
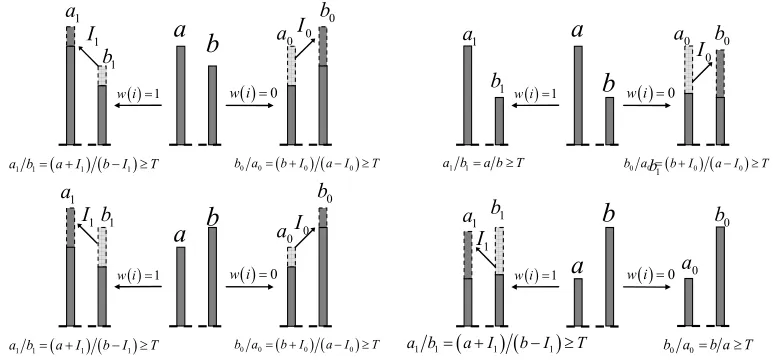
图2 水印嵌入策略
当要嵌入的水印信息为1时,若ab≥T,则不需要调整任何像素。否则,要从灰度值属于bin_2的像素中随机选择I1个像素进行调整,使得调整后的这I1个像素落入bin_1内,从而使调整后的a1=a+I1,b1=b-I1,且满足:a1b1≥T。
当要嵌入的水印信息为0时,若ba≥T,则不需要调整任何像素。否则,要从灰度值属于bin_1的像素中随机选择I0个像素进行调整,使得调整后的这I0个像素落入bin_2内,从而使调整后的a0=a-I0,b0=b+I0,且满足:b0a0≥T。
对像素的调整可按如下规则进行:

f1(i)是从bin_1中随机选取的第i个像素,f2(i)是从bin_2中随机选取的第j个像素,(i)和(i)分别是调整后的像素,且分别落入bin_2和bin_1中。需要调整的像素个数I0和I1可按下式进行计算:
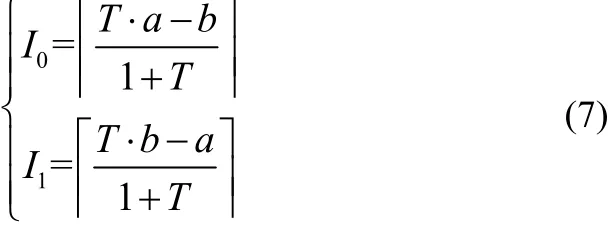
(4)重复步骤(3),通过调整像素值将Lbits水印信息全部嵌入到L个直方图“收集箱”中。
2.2 提取算法
(1)统计待检测图像I’像素值属于灰度范围B'= [N-L,N+L]的灰度直方图H’。其中N的取值如下:
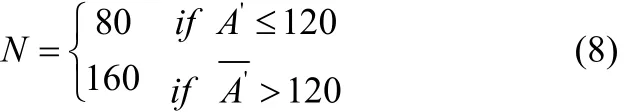
(2)同样将灰度直方图H’的2L个灰度值进行两两分组,共得到L组,即L个“收集箱”。
(3)提取第i组中的水印信息:假设a'(i)和b'(i)分别是第i个“收集箱”中前后两个灰度值的像素个数,则第i位水印信息为:
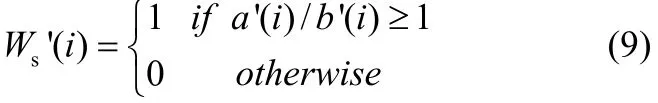
(4)重复步骤(3),提取出嵌入的所有水印信息。然后利用置乱密钥Key将进行恢复置乱得到最终水印信息W'。
3 实验结果与分析
本文取长度为 4 0bit的二值伪随机序列作为水印,用标准灰度Lena图像(256×256)作为原始载体,以Matlab7.0为仿真平台。我们采用峰值信噪比(PSNR)作为水印不可感知性的客观度量指标,采用归一化相关(NC)来度量提取出的水印与原始水印之间的相似性。
3.1 水印隐蔽性测试
图3给出了Lena图像在水印嵌入前后的灰度直方图变换情况。不难发现,水印化图像的直方图对原始直方图进行了局部调整,水印信息正是隐含在了直方图的局部调整之中。图4分别给出了原始Lena图像、嵌入水印后的图像和两者之间的差异图像。水印化图像的PSNR值为55.3685dB。由实验结果可知人类视觉无法感知水印嵌入前后图像之间的失真。因此,本算法具有良好的水印透明性。

图3 Lena原始图像与嵌入水印后的Lena图像直方图

图4 Lena原始图片与嵌入水印后的Lena图片以及嵌入前后的差异图像
3.2 水印鲁棒性测试
我们设计这样一个相关检测器来测试水印的鲁棒性:随机产生1000组相互独立的二值序列(0或1),每组序列的长度等于原始水印序列长度,即40bit。在这1000组随机序列中,任意抽取一组(本文选取第 500组),将其换为原始水印序列。然后分别计算从遭受攻击的水印化图像中提取的水印序列与该 1000组随机序列之间的归一化相关值,来判断是否有水印嵌入。
对嵌入水印后的图像进行了各种几何攻击以考察本算法的鲁棒性。表1给出了本文算法对各种几何攻击的鲁棒性测试结果。可以发现,本算法对RST、改变纵横比和Shearing等仿射变换均具有很强的鲁棒性,原因在于:仿射变换是全局线性变换。它仅仅改变了图像像素的空间位置,但对像素灰度值的调整却并不明显。另外,当图像遭受随机局部剪切攻击后,随机剪切部分和剩余部分的像素值在概率上具有相同或相似的数据分布。从而直方图的形状并不会发生较大幅度的变化。所以本算法对随机剪切攻击也表现出很高的稳健性。图5列出了各种几何攻击下提取的水印序列在相关检测器中的响应情况,其中,(a)~(f)分别是(A)~(F)攻击下提取的水印序列的检测响应。

表1 各种几何攻击下的NC值

图5 各种几何攻击下提取的水印序列在相关检测器中的响应情况
同时,也对含水印的图像进行了椒盐噪声、中值滤波、JPEG有损压缩和直方图均衡化等常规的图像攻击,以测试其鲁棒性。表2列出了相应的测试结果。可以发现,本文算法对椒盐噪声、中值滤波均具有较高的稳健性,原因在于它们并没有过多地改变图像像素值的数据分布。遗憾的是,直方图均衡化攻击下提取的水印的NC只有0.6250。这是由于直方图均衡化使图像像素灰度的概率密度变为了均匀分布,从而大幅改变了图像灰度直方图的形状,势必导致水印提取失败。图6列出了几种常规图像攻击下提取的水印序列在相关检测器中的响应情况,其中,(a)~(c)分别是(A)~(C)攻击下提取的水印序列的检测响应。此外,图7显示了JPEG有损压缩攻击下的测试结果,因为JPEG有损压缩对图像灰度值影响比较大,也构成了本算法的一个严重威胁。因此,本算法对图像整体灰度值改变方面的攻击和操作存在一定的局限性,这也正是我们下一步研究工作的重点。

表2 各种图像处理攻击下的NC值

图6 几种常规图像攻击下提取的水印序列在相关检测器中的响应情况
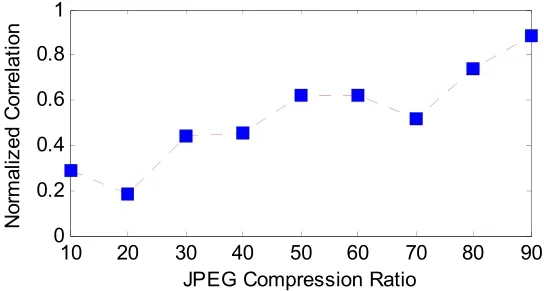
图7 JPEG有损压缩不同比率下的NC值
4 结束语
本文提出了一种基于直方图调整的抗几何攻击数字水印算法。灰度直方图作为灰度图像的一种非常重要的全局统计特征,充分体现了图像像素灰度值与其出现频率的统计关系,而统计特征独立于像素的空间位置,因此它不受由几何攻击引起的像素位置改变以及差值误差的影响。在水印嵌入时可以通过调整参数来合理折中水印鲁棒性与不可见性之间的矛盾。在水印提取时不需要原始图像参与,即实现了盲检测。实验结果表明本算法能有效抗击旋转、尺度变换、平移、裁剪、仿射变换等几何攻击及其组合攻击,而且对常规的图像处理操作也具有较强的鲁棒性。
[1]Sun Gang, Xie Jun-Yuan. Research on a watermark based onthe Fourier-Mellin transform. Computer Engineering.2004.
[2]Shi Lei, Zhong Ming, Hong Fan. Quantization based watermarking robust to geometric transformations. Journal of Computer-aided Design and ComputerGraphics.2004.
[3]Kang X G, Huang J W, Shi Y Q, Lin Y. A DWT-DFT composite watermarking scheme robust to both affine transform and JPEG compression. IEEE Transactions on Circuits and Systems for Video Technology, 2003.
[4]Coltuc D, Bolon P. Watermarking by Histogram Specification[C]//Proceeding of SPIE. Bellingham: Society of Photo- Optical Instrumentation Engineers.1999.
[5]李妍,张佑生,张挺.一种基于直方图的可逆数字水印算法[J].计算机技术与发展.2006.
