关于一类具有垂直传染与治疗SIR模型产生后向分支的研究

段西超,杨艳华（.空军第一航空学院基础部,河南信阳464000；.信阳农业高等专科学校计算机科学系,河南信阳464000）

关于一类具有垂直传染与治疗SIR模型产生后向分支的研究

段西超1,杨艳华2
（1.空军第一航空学院基础部,河南信阳464000；2.信阳农业高等专科学校计算机科学系,河南信阳464000）

考虑了有限治疗资源和垂直传染的一类传染病模型,当染病个体数量小于某确定值时,治疗康复人数与染病个体数成比例；当染病个体数量大于某确定值时,治疗康复人数是确定常数值.确定了模型的基本再生数R0.在一定条件下,当R0＞1时,地方病平衡点E*是渐进稳定的；当R0＜1时,后向分支就产生了.

传染病；后向分支；治疗；垂直传染

许多疾病的传染除了接触传染外还有母婴垂直传染[1],例如：单纯疱疹、乙肝、南美洲锥虫病等疾病[2-3].在昆虫和植物中,垂直传染经常来自虫卵和种子.Busenberg和Cooke研究了一类具有垂直传染和水平传染的传染病模型[4],我们希望通过研究发现,在具有垂直传染和水平传染的传染病模型中产生后向分支.

1 模型的建立

在文献[4]我们看到了标准SIR模型中产生了后向分支,并且都研究了由不同原因导致后向分支的产生[5-6].由此可见,基本再生数不再是描述疾病是否消失的唯一尺度.所以,通过研究后向分支确定控制疾病的阈值显得十分重要.这里有限治疗对产生后向分支起到了至关重要的作用.

将人口分为易感者、染病者和康复者,分别表示为：S,I和R.假定人口出生率和自然死亡率相等都记为d,并假设没有因病死亡人口,所以总人口应该保持常数不变[2]；.有如下模型：

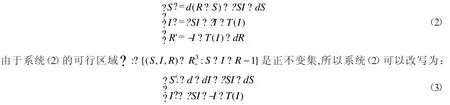
接下来的部分研究系统（2）的后向分支情况和无病平衡点的全局稳定性.

2 平衡点及其稳定性

这部分研究系统（3）的平衡点及其稳定性.E0=（1,0）是无病平衡点.正平衡点应该满足：当0≤I≤I0时,式（4）成立,当I0≤I时,式（5）成立：

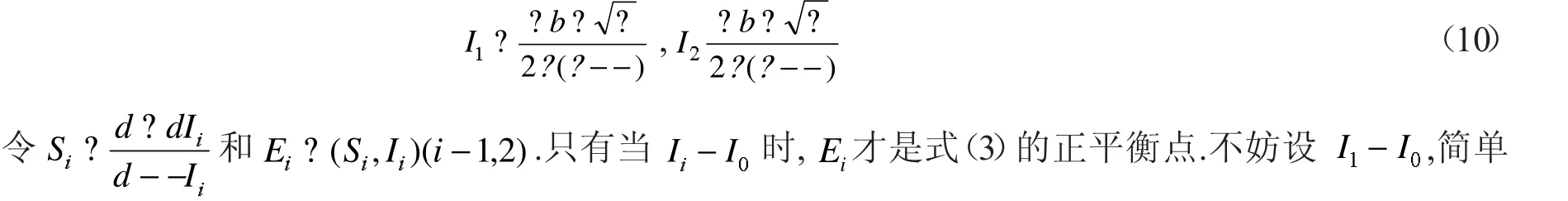
计算可知它等价于

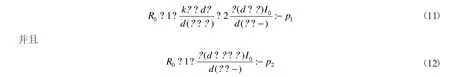
因此,I1＞I0当且仅当p1＜R0＜p2.当p2＜R0或R0＜p1时I1≤I0.类似的讨论可以得到I2＞I0,当R0＞p1时,或者当p2＜R0≤p1时.此外,若R0≤min则有I2≤I0.

综上所述,可得如下定理：

易见,p1＜p2等价于d???(d −−)I0,由此可得到如下定理：

定理2当R0＜p0时,正平衡点E1和E2都不存在.但是当R0≥p0时,有：

对于当R0＜1时,系统产生正平衡点即后向分支有很好的实际意义.下面的推论将给出系统产生后向分支的条件.

推论当R0＜1时,如果d???(d −−)I和P0＜1成立,那么系统（3）将产生后向分支.

这个推论只是定理2中（1）部分的另一种表述方式.下面讨论平衡点的稳定性,有如下定理.

定理3若R0＜1,E0=（1,0）是渐进稳定的；若R0＞1,E0=（1,0）是不稳定的.若I*＜I0,E*=（S*,I*）是渐进稳定的.若E1存在,则它是一个鞍点,对于E2,有

证明：参见文献[4]和定理1.

通过构造Dulac函数,参见文献[4]可以证明无病平衡点E0的全局稳定性,有如下定理：

定理4如果下列条件满足,E0=（1,0）是全局稳定的.

（1）R0＜1且p0＞1；（2）R0＜1,p0＜1,且p1＞1.

3 讨论

本文我们研究了一类传染病模型.对这类模型,假定没有因病死亡,且假设出生率与自然死亡率相等,这就保证了总人口处于恒定不变的状态.进而,使得医疗水平保持不变这一条件变得更贴近现实.推论明确揭示了后向分支的产生源自有限的治疗水平,同时也说明了当基本再生数小于1时,不一定保证疾病的消失.这就预示着染病个体必须控制在一定阈值条件以下.否则,在一定条件下疾病就会处于弱持续生存状态.

[1]Michael Y L,Smith H L.Global dynamic of an SEIR epidemic modelwith vertical transmission[J].SIAM J.Appl.Math,2001,62（1）：58-69.

[2]Bellenir K,Dresser P.Contagious and Non-Contagious Infectious Diseases Sourcebook[M].Detroit.：Health Science Series. Omnigraphics Inc.,1996.

[3]Busenberg S,Cooke K.Vertically Transmitted Diseases[M].Berlin,New York：Springer-Verlag,1993.

[4]WangW.Backword bifurcation ofan epidimicmodelwith treatment[J].Math.Biosci,2006,201：58-71.

[5]Arino J,McCluskey CC,den Driessche P.Global results foran epidemicmodelwith vaccination thatexhibitsbackward bifurcation [J].SIAMJ.Appl.Math.,2003,64：260-275.

[6]Dushoff J,HuangW,Castillo CC.Backward bifurcationsand catastrophe in simplemodelsof fataldisease[J].J.Math.Biol,1998,36：227-242.

（责任编辑：卢奇）

Backward bifurcation of an SIR epidem icmodelw ith treatment and vertical transm ission

Duan Xichao1,Yang Yanhua2
（1.The FirstAeronauticalCollegeof Air Force,Xinyang464000,China；2.Xinyang Agricultural College,Xinyang 464000,China）

An epidemicmodel that incorporates a limited resource for treatment and vertical transmission have been considered.The total host population is assumed to have constant density.It is assumed that treatment rate is proportional to the number of infectivities below the capacity and is a constantwhen the number of infectivities is greater than the capacity.The basic reproduction number of the disease R0is found.If R0＞1 the endemic equilibrium E*is asymptotically stable under some conditions.If R0＜1 a backward bifurcation occurs.

epidemic,bifurcation,treatment,vertical transmission.

Q332

A

1008-7516（2011）05-0047-04

10.3969/j.issn.1008-7516.2011.05.012

2011-07-08

段西超（1982-）,男,河南许昌人,硕士,讲师.主要从事生物数学研究.