人造机械瓣心音的分析研究

张 地 姚尖平 杜明辉 杨 嵩

1(韶关大学计算机科学学院，韶关 512002)

2(中山大学附属第一医院心脏外科，广州 510080)

3(华南理工大学电子与信息学院，广州 510641)

引言

听诊是利用听诊器听取心脏所发出的声音来帮助诊断各种心脏疾病的一种有效手段。在一些致命性心脏病的诊断中，心音听诊是最有效、最便宜也是应用得最成功的手段之一。一些研究表明，听诊的敏感度比使用超声心音检查法和荧光摄影检查法要高出92%。但是，心音所包含的全部信息并不能轻易被人耳所听取和辨析。例如，人耳对频率改变的敏感度要比对强度改变的敏感度要高，因而导致声波实际上的频率改变往往被误辨为强度的改变。因而，仅凭借传统上的听诊手段，要做出正确的判断并不是一件容易的事情，往往在很大程度上取决于医生的经验和其听觉的灵敏度。为了改变这种状况，信号处理和模式识别技术就被尝试引入到听诊当中来。

迄今为止，研究人员针对天然瓣膜心音的自动诊断做了大量的研究工作［1-6］，取得了一定的成效。其中，Gupta等先利用小波来提取心音特征，再利用人工神经网络(ANN)将心音分为3类，总的分类准确率达到了96%［1］。Uguz等同时利用小波和短时傅里叶变换来提取特征，并使用隐马尔可夫模型将心音分为正常/异常两类，取得了特异性(specificity)和敏感性(sensitivity)分别为92%和97%的结果［2］。刘军等也做了类似的尝试［3］。周静等从小波、香农能量分布等方面着手提取心音的特征，以用于识别不同的心音信号，并进行了仿真验证［4］。Vos和 Blanckenberg运用 Jack-knife方法来训练ANN分类器，获得了高达99%以上的特异性和敏感性［5］。最近，Dokur和 Ölmez又提出了一种基于小波的特征提取办法提取了14种天然瓣膜心音的特征，以期获得较好的分类效果［6］。但从本质上说，这些分析及特征提取都是基于心音信号为平稳或分段平稳的假设，需要用到虚假的高频成分来补偿信号的非平稳性，从而引起能量的扩散，以致给出信号的错误解释。为此，赵治栋等和李杉杉等运用希尔波特-黄变换(Hilbert-Huangtransform，HHT)，对心音信号进行分析处理，取得了较好的效果［7-8］。

但是，对于人造瓣膜心音而言，有关的文献报道则较少。目前，使用的人造瓣膜主要有两种:生物瓣和机械瓣。对于生物瓣，最早的频谱分析报道于1981年，其中详细分析了置换生物瓣后第一心音的频率成分［9］。随后，Akay等系统地比较了正常/异常生物瓣心音的频谱差异［10］。Bentley等首次尝试使用频谱分析和小波分析来提取心音特征，并对生物瓣心音进行正常/异常分类，但效果不太理想，准确率只有60% ～70%［11］。对于机械瓣的研究，Koymen等首先提出了一个模型来解释植入机械瓣后的心音特征［12］。Sava等全面比较了机械瓣植入前后心音的频谱变化情况［13］。Sugiki等使用了连续小波变换，分析机械瓣心音的声学特征［14］。但一直到最近，才有对正常/异常机械瓣心音的研究报道发表［15］。在文献［15］中，张地等分析了正常和两种异常机械瓣心音的频谱特征和时频特征，并指出可以通过这些特征，对机械瓣心音进行正常/异常分类。

目前，在中国机械瓣的使用非常普遍，但关于其病变判别的研究还很欠缺，所以研究简单有效的机械瓣病变判别方法，对于临床诊断来讲具有很大的意义。笔者运用 HHT，对已经发现的全部5种(正常和4种异常)机械瓣心音进行了详细分析，并提出了一种基于HHT的特征提取办法。实验证明，该方法对5种不同心音进行识别，具有很好的识别效果。

1 心音数据和方法

1.1 心音数据

心音数据录自机械瓣膜已经置换了3个月以上的病人。对于每一个目标病人，使用接触式心音传感器，在病人处于心绪平静状态时进行心音录取。录取时的采样频率设置为8 000 Hz，分辨率为16位。整个心音的录取过程由有经验的心脏外科医生进行，心音的所属类型最终用彩色多普勒超声诊断仪进行确认。

对总计5种不同的机械瓣心音进行研究，包括有:正常 (normal，NOR)、瓣周漏 (perivalvular leakage，PL)、卡瓣(valve obstruction，VO)、瓣狭窄(valve stenosis，VS)、瓣狭窄 +瓣周漏(VSPL)。心音数据库中有100个正常和50个异常病人的心音，其中50个异常的分布情况为:13例 PL，9例 VO，16例 VS，12例 VSPL。

1.2 方法

采用的研究流程如图1所示，以下按照流程顺序依次进行说明。

1.2.1 预处理

所有心音先用一个四阶Butterworth IIR高通滤波滤波器水，再用一个十阶 Butterworth IIR低通滤波器进行滤波，以滤除原始心音中包含的高频和低频噪声。随后的去噪处理包含 3个步骤［16］:使用db5对心音进行八阶小波包分解→对每一阶分解系数进行阀值判比→用判比后的系数进行重构。

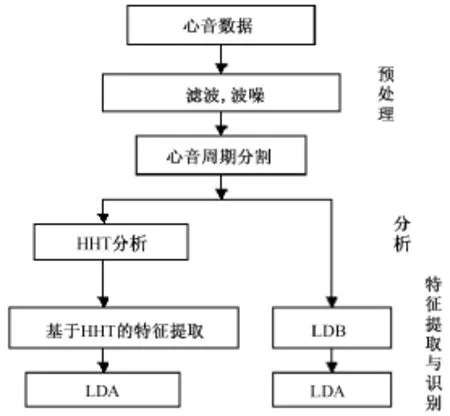
图1 分析和分类流程Fig.1 Analysis and classification scheme

因关注的是机械瓣心音的分析及识别，所以在心音分割方面采用了文献［6］提出的方法。分割后的5种不同的机械瓣心音见图2，显示了一个完整的心音周期中接触式心音传感器的输出强度，采样频率为8 000 Hz。

1.2.2 HHT 分析

HHT方法非常适用于分析非平稳信号，主要由经验模式分解(EMD)和希尔伯特(Hilbert)变换两部分组成。一般信号中包含有多种振荡模式，直接对其进行希尔伯特变换得到的瞬时频率毫无意义。而EMD基于信号的局部特征时间尺度展开，将其分解为一些内蕴模式函数(IMF)的组合，IMF能给出瞬时频率有意义的物理解释。对IMF进行Hilbert变换，获得的瞬时频率及振幅都是时间的函数。时间-频率-振幅就构成了信号的 Hilbert谱，无论在时域还是在频域，都具有良好的分辨率，并且三维的分布能够反映出信号的内在本质特征。

给定原始信号x(t)的各个IMF分量xj(t)，j=1，2，…，n。如果对每一个 IMF进行 Hilbert变换，得到相应的yj(t)。xj(t)和yj(t)可组成一个复解析信号 zj(t)=xj(t)+iyj(t)(j=1，2，…，n)。令该解析信号的幅度和相角分别为aj(t)和θj(t)，则瞬时频率可以定义为

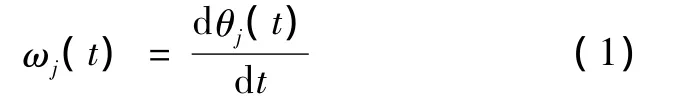
而原始信号x(t)可以表达为

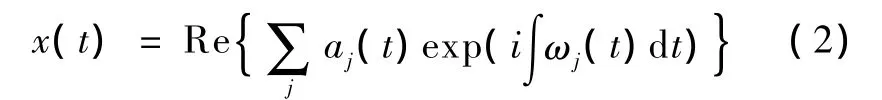
由于幅度和瞬时频率皆为时间的函数，所以可将幅度与瞬时频率随时间的变化表示在一个三维结构中，即在联合的时间频率平面上将幅度表现出来。这种幅度的时间-频率分布被定义为原始信号x(t)的 Hilbert谱，一般用 H(ω，t)表示为

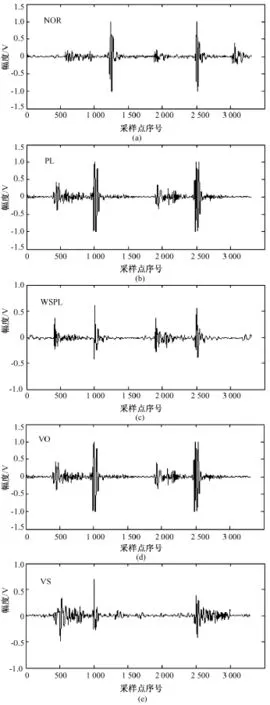
图2 5种不同机械瓣心音的一个心音周期Fig.2 A complete cycle of 5 different heart sounds

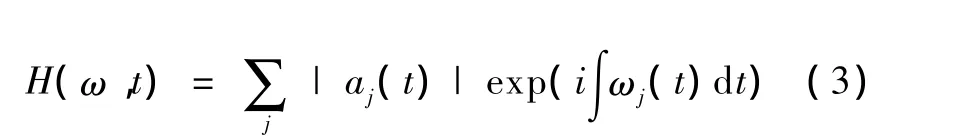
进一步可以定义边界谱为

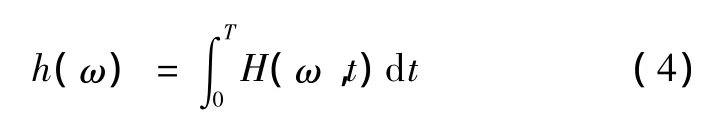
1.2.3 特征提取与识别

特征提取是模式识别过程中一个非常重要的步骤。如果所提取的特征分类性能不好，则分类器的性能将急剧下降。特征提取同时也要将特征向量的维数降低到一个合理的水平，以只包含那些对分类最有用的类间差异信息。研究了基于HHT和LDB这两种不同的特征提取方法对机械瓣心音的分类效果。

基于HHT的特征提取可以通过下列步骤完成。

步骤1:对原始机械瓣心音信号EMD分解，得到 K阶 IMF。

步骤2:计算K阶IMF的平均过零率，得到K个特征。

步骤3:计算K阶IMF的Hilbert边界谱。将各阶边界谱按频率轴分别划分为 Di(i=1，2，…，K)个区间， 计算各阶边界谱在频率轴上按区间Di的归一化分布，得到个特征。

利用HHT提取机械瓣心音特征的具体参数选择如下:

1)计算前5阶IMF的平均过零率作为5个特征参数。

2)计算前5阶的 Hilbert边界谱。将一阶边界谱从0～400 Hz等距划分为10个频段，将二阶边界谱从0～200 Hz等距划分为10个频段，将三阶边界谱从0～100 Hz等距划分为10个频段，将四阶、五阶边界谱从0～50 Hz等距划分为5个频段，分别统计各阶边界谱在各个频段上的能量并分别归一化，总共得到40个特征参数。

每个机械瓣心音经上述处理后总计提取45维的特征参数用于分类。

最早由Saito和 Coifman提出局部最优基(local discriminant bases，LDB)方法［17］，其实质上就是一个特征提取算法。LDB算法通过对信号进行小波包分解，从所得到的正交基集合中选取具有最大可分度测度(例如相对熵等)的正交基组合来做为分类的特征。更具体地说，给定一个含有C类样本的训练集，LDB算法通过如下步骤来选择局部最优基。

步骤1:选择一个合适的小波母函数，确定最大的分解层数J和可分度测度函数D。

步骤2:计算小波包分解二叉树中每一个节点的D值。

步骤3:如果父节点的D值大于其两个子节点的D值的和，则保留父节点;否则保留两个子节点。该比较选择过程按照从底部往上的顺序进行，直到到达根节点。

步骤4:将上一步中所得到的正交基按照D值的大小顺序排列，取其中具有最大D值的k个(一般k小于或等于原始信号的维数)正交基特征。作为特征矢量输入到分类器进行识别。

对于LDB算法，本研究使用 db6小波、6级分解，并同样选择前45个具有最大可分度测度的特征。由于机械瓣异常心音的数量有限，这里采用了留一法(leave-one-out)来训练和测试分类器。

2 结果

图3～图7分别给出了5种不同机械瓣心音的前4阶IMF及对应的Hilbert边界谱。从中可以看出，尽管所有机械瓣心音的Hilbert边界谱随着筛选层数的增加而逐渐向低频端靠拢，但不同机械瓣心音的各阶能谱分布还是有很大的区别。对于一阶Hilbert边界谱而言，首先，注意到 NOR心音与其他心音最显著的差别在于其沿频率轴分布得比较散，从0～400 Hz基本上都有显著的能量分布，其他心音则大多集中在200 Hz以下;其次，VO、VS心音的一阶谱集中在100 Hz以下，而 PL、VSPL的一阶谱则大致以100 Hz为中心呈对称分布。对于二阶Hilbert边界谱而言，PL心音是一条非常显著的双峰曲线，两个波峰分别位于25和100 Hz附近;而其他心音则基本上可以近似地被认为是一条单峰曲线(VSPL心音虽然有两个峰，但其第二峰相对于能谱基底的比值不大，没有PL心音那么显著)。对于三阶Hilbert边界谱而言，NOR心音是一条双峰曲线，峰值位于30和40 Hz附近;其他心音则是一条单峰曲线，峰值位于20和30 Hz之间。对于四阶Hilbert边界谱而言，NOR心音的能量主要集中在20 Hz附近;PL和VS心音的能量主要分布在5～15 Hz之间，VO心音的能量主要集中在15 Hz附近，VSPL心音的能量则分布在0～25 Hz之间。不同机械瓣心音的Hilbert边界谱这些差异，证明了所提出的基于HHT边界谱特征提取的可行性。

为了对比Hilbert边界谱与常规频谱在分析机械瓣心音时的差异，图8给出了采用特征向量法(eigenvector)所得到的功率谱。从中可以看出，此时只能根据能谱分布，有效鉴定出具有双峰特征的PL心音，而PL心音能谱的双峰特征在HHT分析的二阶 Hilbert边界谱中得到了证实。但对于在HHT分析中所获得的分类其他心音的有效特征，Eigenvector功率谱则无能为力。这是由于一般的谱估计法是基于信号为平稳或分段平稳的假设上进行的，以致给出了信号的错误解释。

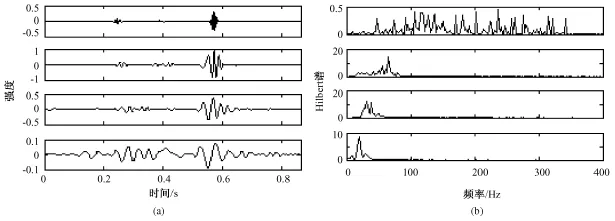
图3 NOR心音的IMF和对应的Hilbert边界谱。(a)前4阶IMF;(b)Hilbert边界谱Fig.3 IMF and the corresponding Hilbert spectrum for NOR heart sound，(a)the 1st～ 4thorder of IMF;(b)Hilbert spectrum

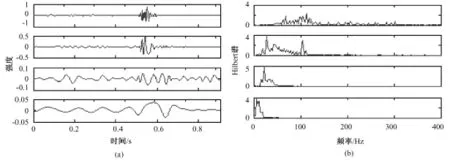
图4 PL心音的IMF和对应的Hilbert边界谱。(a)前4阶IMF;(b)Hilbert边界谱Fig.4 IMF and the corresponding Hilbert spectrum for PL heart sound，(a)the 1st～ 4thorder of IMF;(b)Hilbert spectrum

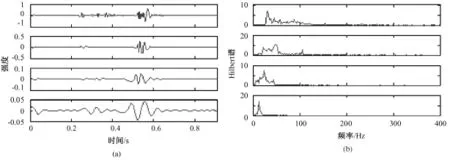
图5 VO心音的IMF和对应的Hilbert边界谱。(a)前4阶IMF;(b)Hilbert边界谱Fig.5 IMF and the corresponding Hilbert spectrum for VO heart sound，(a)the 1st～ 4thorder of IMF;(b)Hilbert spectrum

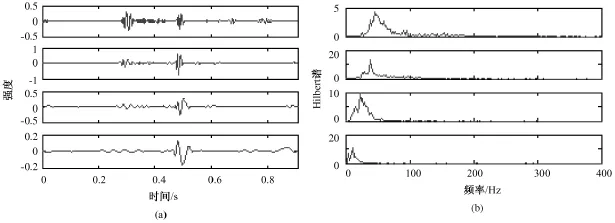
图6 VS心音的IMF和对应的Hilbert边界谱。(a)前4阶IMF;(b)Hilbert边界谱Fig.6 IMF and the corresponding Hilbert spectrum for VS heart sound，(a)the 1st～ 4thorder of IMF;(b)Hilbert spectrum

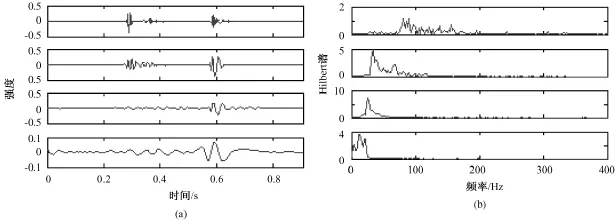
图7 VSPL心音的IMF和对应的Hilbert边界谱。(a)前4阶IMF;(b)Hilbert边界谱Fig.7 IMF and the corresponding Hilbert spectrum for VSPL heart sound，(a)the 1st～4thorder of IMF;(b)Hilbert spectrum

图8 使用特征向量法得到的功率谱Fig.8 Power spectrum using Eigenvector method

表1给出了两种特征提取方法与LDA分类器结合后的分类效果。从中可以看到，采用HHT+LDA和LDB+LDA总的识别率分别是97.3%(146/150)和91.3%(137/150)，可见采用 HHT提取特征要优于 LDB算法。另外值得注意的是，HHT+LDA可以完全将 PL、VO和 VS这3种心音鉴别出来，而LDB+LDA只能正确鉴别VO心音。表1的结果还表明，经典的LDB算法在很多情况下还有待改善:譬如能用功率谱估计所能鉴定出来的VO心音，LDB+LDA分类器却不能达到100%的识别率。导致这种情况的发生，应该是由于LDB算法在整个正交基的筛选过程中都涉及了求和或求平均的操作，从而造成有用分类信息的丢失。

3 结论

对于心音这种典型的非平稳信号，本研究运用HHT对已经发现的5种机械瓣心音进行了详细分析，并提出了一种基于HHT的特征提取办法。实验证明，该方法对5种不同心音的识别具有很好的效果，比传统的LDB算法在识别率上提高了约6%，达到了97.3%。与LDB算法相比，基于HHT的特征提取方法目前还存在明显的不足:在特征提取上还没有一套行之有效的、系统的方法，最后的识别效果在很大程度上依赖于研究人员的专业知识和不断的尝试。因此，对于HHT而言，获得一套规范化的特征提取方法是一个值得进一步研究的方向。

表1 对两个分类器进行测试后的结果Tab.1 Classification results using two different classifiers

［1］Gupta CN，Palaniappan R，Swaminathan S，et al.Neural network classification of homomorphic segmented heart sounds［J］.Appl.Soft Comp，2007，24(7):286-297.

［2］Uguz H，Arslan A，Turkoglu I.A biomedical system based on hidden Markov model for diagnosis of the heart valve diseases［J］.Pattern Recognition Letters，2007，28(4):395-404.

［3］刘军，张祖兴，潘家华，等.基于短时傅立叶变换和连续小波变换的先天性心脏病心音比较分析研究［J］.云南大学学报，2006，28(s1):89-93.

［4］周静，杨永明，何为.心音信号的分析及其特征提取方法的研究［J］.中国生物医学工程学报，2005，24(6):685-689.

［5］Jacques PV，Mike B.Automated Pediatric Cardiac Ausculation［J］.IEEE Trans Biomedical Engineering，2007，54(2):244-252.

［6］Dokur Z，Ölmez T.Feature determination for heart sounds based on divergence analysis［J］.Digital Signal Processing，2009，19(3):521-531.

［7］赵治栋，唐向宏，赵知劲，等.基于Hilbert-Huang Transform的心音信号谱分析［J］.传感技术学报，2005，18(3):18-22.

［8］李杉杉，袁中凡，杨春生.改进HHT算法及在心音信号分析中的应用［J］.四川大学学报，2007，39(4):160-163.

［9］Stein PD，Sabbah HN，Lakier JB，et al.Frequency of the first heart sound in the assessment of stiffening of mitral bioprosthetic valves［J］.Circulation，1981，63(1):200-203.

［10］Akay M，Semmlow JL， Welkowitz W，et al. Noninvasive detection ofcoronary occlusionsusing Eigenvectormethods before and after angioplasty［J］.IEEE Trans Biomedical Engineering，1990，37(11):1095-1108.

［11］Bentley PM，Grant PM，and McDonnell JTE.Time-frequency and time-scale techniques for the classification of native and bioprosthetic heart valve sounds［J］.IEEE Trans Biomedical Engineering，1998，45(1):125-128.

［12］Koymen H，Altay BK，Ider YZ.A study of prosthetic heart valve sounds［J］.IEEE Trans Biomedical Engineering，1987，34(11):853-863.

［13］Sava HP，McDonnell JTE.Spectral Composition of heart sounds before and after mechanical heart valve implantation using a modified forward-backward Prony’s method［J］.IEEE Trans Biomedical Engineering，1996，43(7):734-742.

［14］Sugiki H，Shiiya N，Murashita T，et al.，Wavelet analysis of bileaflet mechanical valve sounds［J］.Journal of Artificial Organs，2007，10(6):16-21.

［15］Zhang D，Yao JP，Yang S，et al.Detection of mechanical heart valve dysfunction using spectrum estimation and time-scale techniques［C］//Proceedings of IEEE Pacific-Asia Workshop on Computational Intelligence and Industrial Application(PACIIA).Wuhan:IEEE，2008:827-831.

［16］Hall L，Maple J，Agzarian J，et al.Sensor system for heart sound bio-monitor［J］.Journal of Microelectron，2001，31(8):583-592.

［17］Saito N， Coifman RR.Local discriminant bases and their applications［J］.Journal of Mathematical Imaging and Vision，1995，5(3):337-358.