船舶航迹跟踪的滑模控制

邢道奇 张良欣

（海军工程大学 后勤指挥与工程系 天津 300450）

0 引 言

由于对船舶控制要求的不断提高，船舶航向控制已经不能满足实际需要，从而促使航迹跟踪控制研究成为船舶控制的研究热点。

根据期望航迹是否为时间的函数，船舶航迹跟踪可分为路径跟踪 （path tracking）和轨迹跟踪（trajectory tracking）。路径跟踪不需考虑时间的静态几何位置跟踪，而轨迹跟踪则要求实时跟踪时变的期望轨迹，其跟踪控制的实现比路径跟踪困难得多［1］。同时，由于船舶运动具有惯性大、非线性、模型参数不确定以及存在扰动等特点，因此船舶航迹控制成为了一个非线性问题，若采用线性的船舶模型，则会对航迹跟踪控制性能产生影响，难以满足控制要求。故本文采用非线性船舶模型进行船舶轨迹跟踪控制器设计。

滑模控制器因其具有对系统参数摄动和外界干扰的强鲁棒性，以及控制计算量小、实时性强、快速性好等特点，在解决船舶非线性控制问题上，得到了广泛地运用［2，3］。 本文将滑模控制方法［4］引入到船舶轨迹跟踪控制中，采用指数趋近律进行滑模控制器设计，对动态直线轨迹和环形轨迹的跟踪控制进行了仿真试验，以验证所设计的滑模控制器的有效性。仿真结果表明：滑模控制器的轨迹跟踪控制性能良好，能精确跟踪船舶航迹。

1 船舶非线性数学模型［5］

虽然船舶在海洋中实际运动时通常具有6个自由度，但是，对大多数船舶运动及其控制问题而言，仅考虑3个自由度的平面运动是可行的。因此，本文以船舶平面运动方程为基础，研究船舶轨迹控制问题。

向量 η=［x，y，ψ］T表示地球 NED 坐标系中船舶的位置和首向角，向量 v=［u，v，r］T表示船体坐标系中船舶的纵向速度、横向速度和首向角速度。

地球NED坐标系和船体坐标系之间转换的运动学方程为：

船体坐标系中的船舶平面运动方程为：

其中，坐标系转换矩阵为：

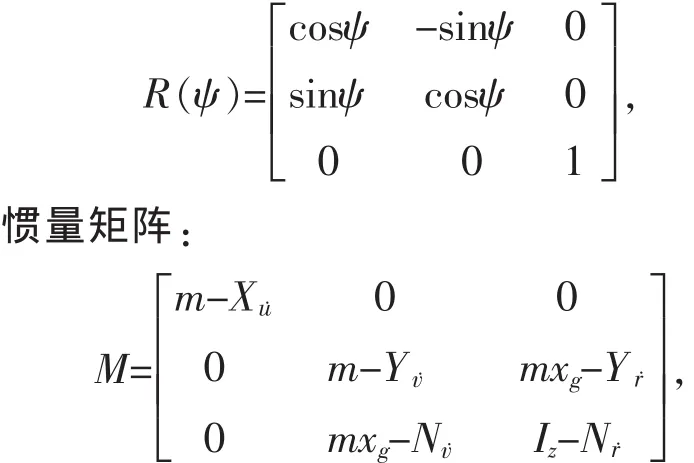
科氏和向心力矩阵为：

阻尼矩阵为：

式中：τ=［τ1，τ2，τ3］T分别是纵向和横向推进力和转向力矩的控制输入，c1=（m-Yv˙）v+（mxg-Yr˙）r，c2=m-Xu˙，xg为船体坐标系中船舶重心在x轴方向上的坐标值，Xu、Xu˙、Yv、Yv˙、Yr、Yr˙、Nv、Nr、Nv、Nr、Iz为船舶水动力参数。

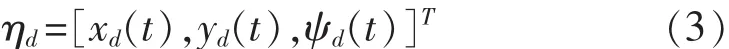
定义地球坐标系中的动态期望轨迹为：xd（t）、yd（t）和 ψd（t）分别为 t时刻船舶的期望位置和首向角。

2 航迹跟踪的滑模控制器设计

2.1 滑模控制器设计

由式（1）可得：

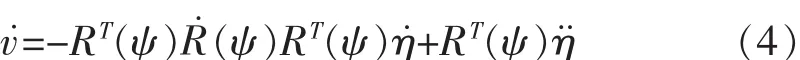
将式（4）代入式（2）中，船舶动力学方程变为：

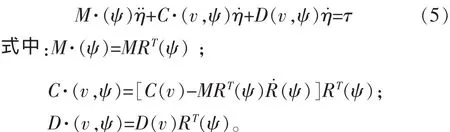
定义轨迹跟踪误差量［5］为：

假设期望轨迹 ηd，和光滑且有界，定义虚拟期望轨迹为：

式中：Δ＞0为正定的设计对角矩阵。

设计船舶跟踪控制的滑模面为：

由式（5）、（9）得：

定义滑模控制规律为［3］：

式中：τe为等效控制，τs为切换控制。

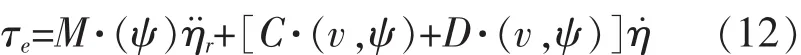
为了快速到达滑模面，考虑指数趋近律：

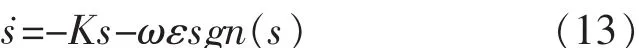
式中：设计控制矩阵 K=diag{k1，k2，k3}；

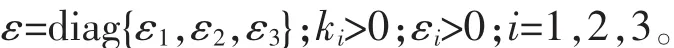
由式（10）～（13）可得切换控制为：

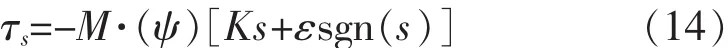
由式（11）、（12）、（14）得滑模控制器控制规律为：

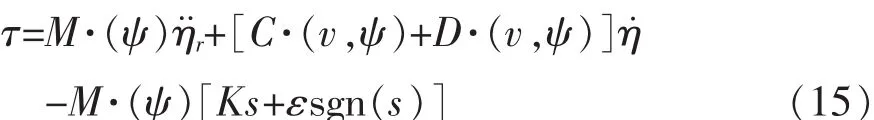
由式（15）可设计船舶航迹跟踪的控制框图，如下页图1所示。

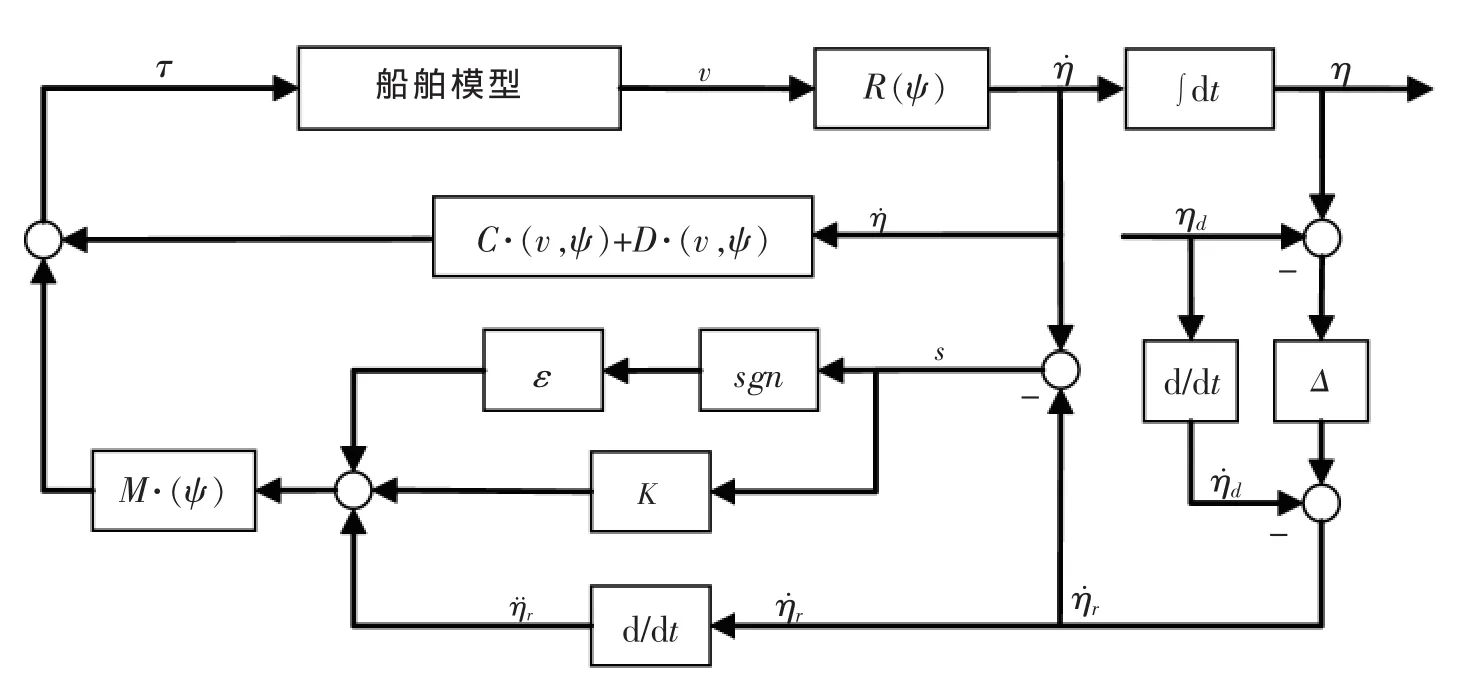
图1 船舶航迹跟踪的控制框图

2.2 稳定性分析

定义 Lyapunov 函数［4，6］为：

由于惯性矩阵M是正定的，由推导可知M·（ψ）是可逆的，则式（10）变为：

将式（15）代入上式可得：

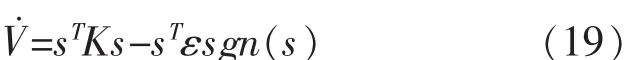
设计参数矩阵 K=diag{k1，k2，k3}和 ε=diag{ε1，ε2，ε3}是 3×3正定对称矩阵，可得：

即对于船舶运动非线性方程式（1）、（2），设计其滑动模态，如式（9）；相应的滑模控制规律为式（15），则滑动模态是渐近稳定的，且跟踪误差趋于0。

3 仿真试验

以挪威科技大学全驱动模型船CybershipⅡ为仿真对象［7］，采用图1所示的控制规律，对其进行航迹跟踪控制仿真，模型船主要参数见表1。

滑模控制器参数设计 为：Δ=diag{15，15，15}，K=diag{1，1，1}，ε=diag{0.01，0.01，0.01}

3.1 仿真试验1

选择期望轨迹为：ηd=［t，t，0］T， 船舶初始状态

12为：η0=［80 m，10 m，20°］T。 即期望轨迹相当于模型船以0°的首向角，沿直线Y=X航行。由图2、3可看出船舶能够较好地跟踪期望轨迹，控制效果良好。

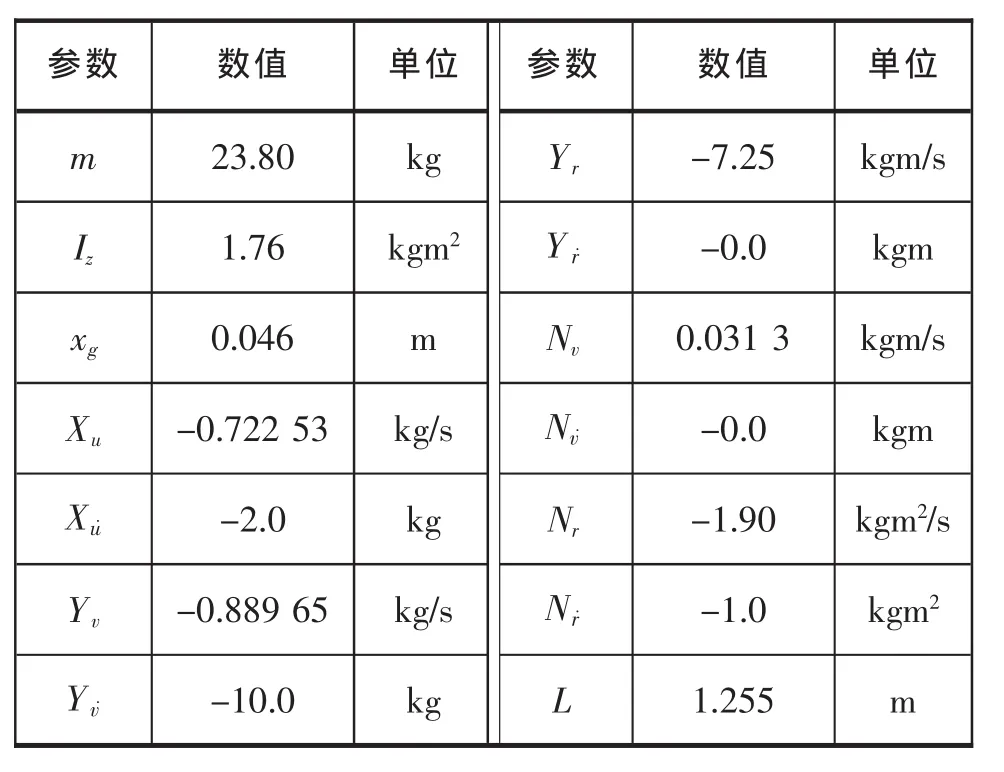
表1 模型船主要参数

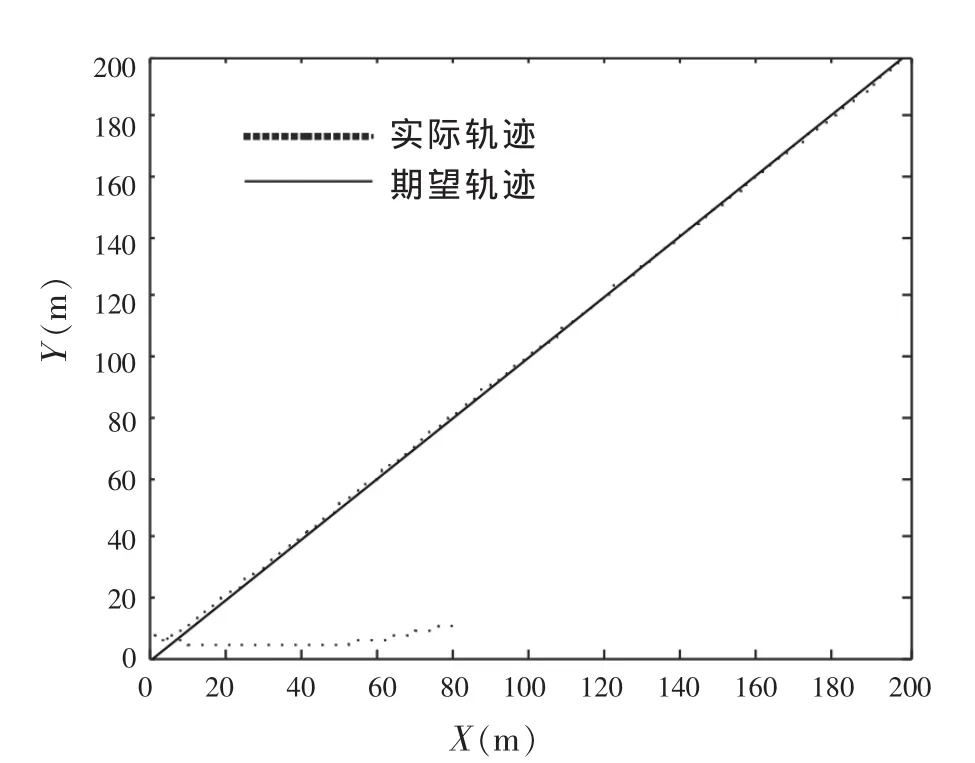
图2 船舶轨迹跟踪曲线

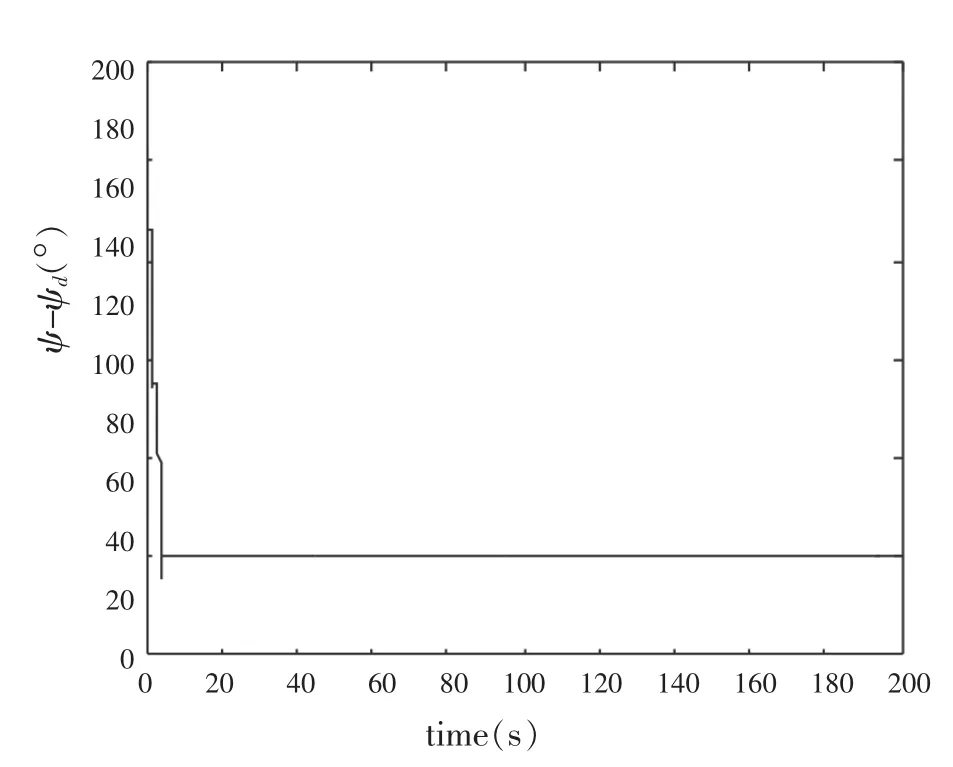
图3 首向角的跟踪误差

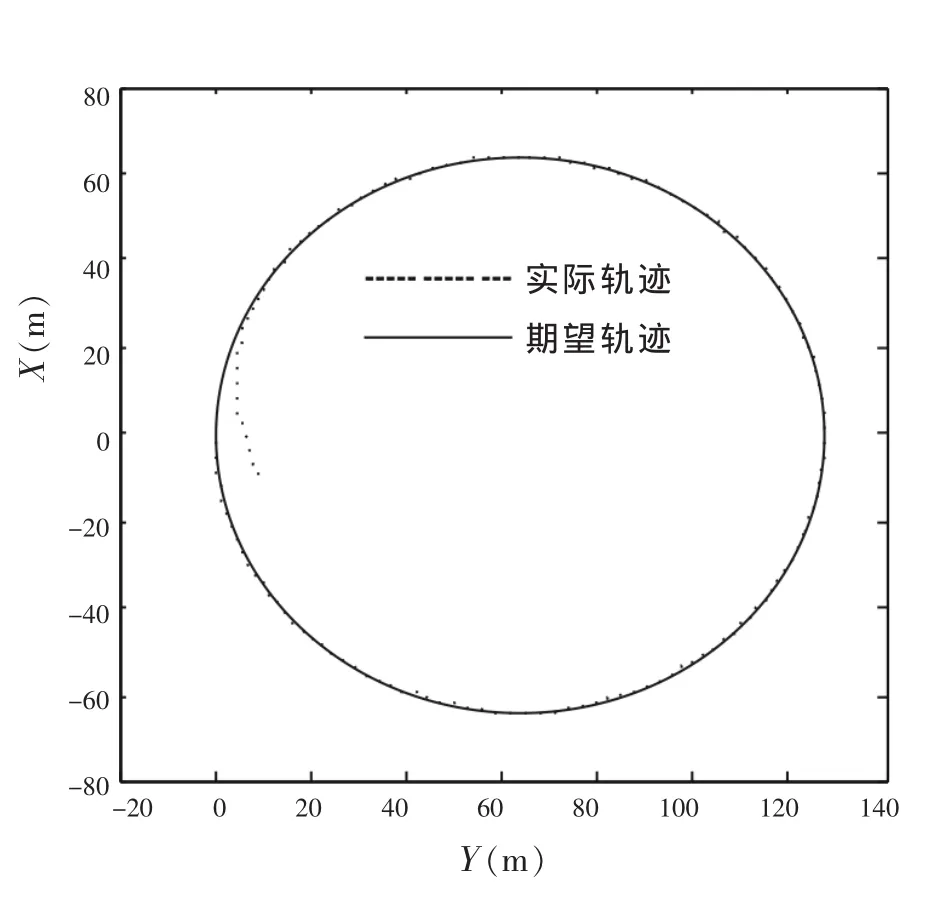
图4 船舶轨迹跟踪曲线

图5 位置X的跟踪比较

3.2 仿真试验2

在仿真中，给定期望轨迹为：

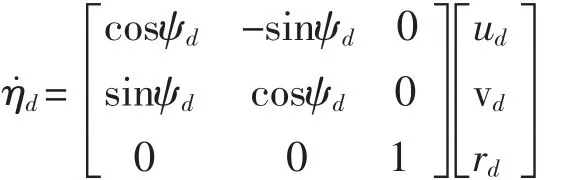
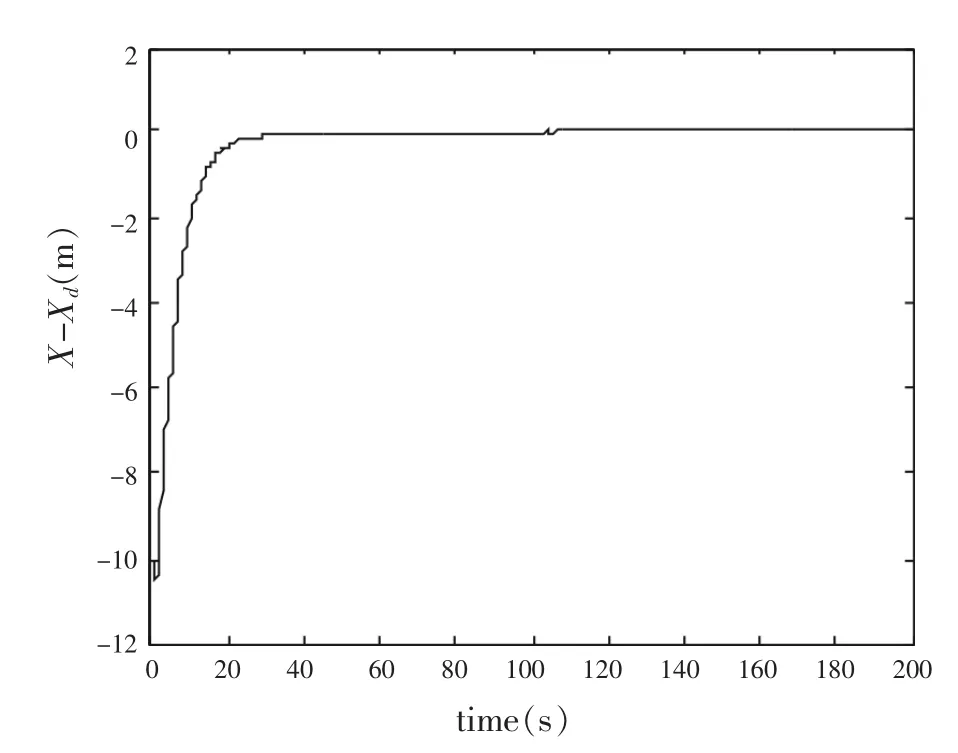
图6 位置X的跟踪误差

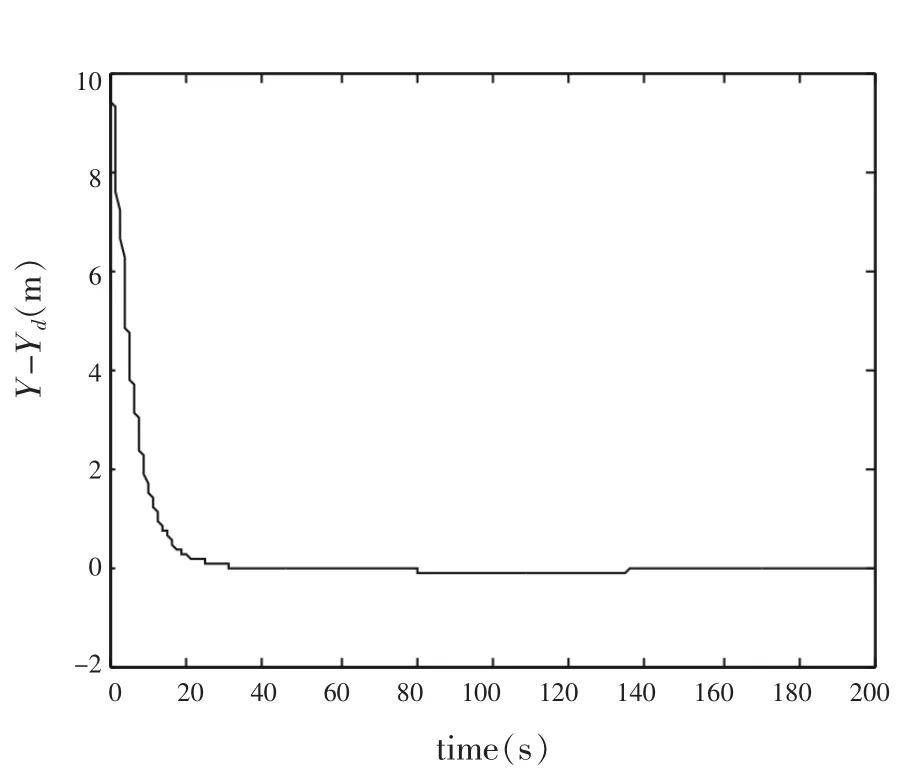
图7 位置Y的跟踪误差

式中：ud＝2 m/s、vd=0 m/s、rd=0.01π（rad/s），即期望轨迹相当于模型船以2 m/s的速度、沿半径为200/π（m）的圆航行，初始位置设为：η0=［-10 m，10 m，10°］T。

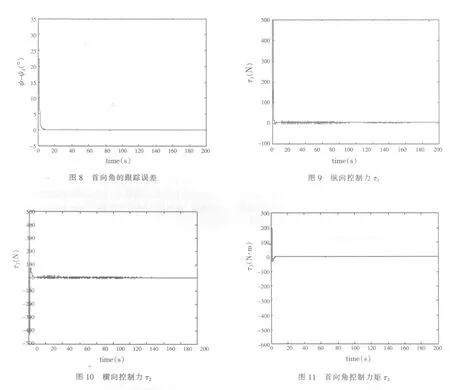
从图4～8可看出，船舶可快速精确跟踪期望轨迹，使跟踪误差趋近于0，跟踪控制性能良好。下页中图9～11是船舶纵向、横向控制力和首向角力矩曲线。从中可以看出，控制输入经过较大调整后，快速趋近于相对稳定的状态。但是由于滑模控制固有的局限，控制输入出现了抖振。如何抑制轨迹跟踪控制中的抖振是今后研究中需要解决的问题。

4 结 语

本文建立了全驱动船舶非线性平面运动方程，设计了船舶轨迹跟踪的滑模控制器，以全驱动模型船Cybership II为仿真对象，对2种期望动态轨迹跟踪控制进行了仿真试验，仿真结果验证了滑模控制器的有效性，跟踪控制性能良好。

［1］郭晨，汪洋，孙富春，等.欠驱动水面船舶运动控制研究综述［J］.控制与决策.2009，24（3）：321-329.

［2］Fahimi F.Sliding-Mode Formation Control for Underactuated Surface Vessels［J］.IEEE TRANSACTIONS ON ROBOTICS.2007，23（3）：617-622.

［3］Alfaro-Cid E，Mcgookin E W，Murray-Smitha D J，et al.genetic algorithmsoptimization ofdecoupled Sliding Mode controllers：simulatedandreal results ［J］. Control Engineering Practice.2005，13：739-748.

［4］胡跃明.变结构控制理论与应用［M］.北京：科学出版社，2003.

［5］Fossen T I.Marine Control Systems：guidance，navigation and control of ships，rigs and underwater vehicles ［M］.Trondheim，Norway：Marine Cybernetics，2002.

［6］高为炳.变结构控制理论基础［M］.北京：科学技术出版社，1990.

［7］Skjetne R.The Maneuvering Problem［D］.Norwegian University of Science and Technology，2005.