船舶非线性横摇运动方程的线性化研究

李 浩 陆建辉

（中国海洋大学 工程学院 青岛 266100）

0 引 言

船舶在风波流等外在激励的的扰动下，会产生各种摇荡运动，剧烈的摇荡还将危及船舶航行的安全。大幅度横摇是导致风浪中航行船舶失稳倾覆的最重要因素之一，也是最为复杂的力学问题［1］。船舶的大幅横摇是一个强非线性的水动力学问题，其非线性包括：恢复力矩的非线性、阻尼力矩的非线性及多自由度运动的非线性耦合和严酷风浪条件的非线性扰动等［2］。为了进行船舶倾覆的概率预报，人们首先想到利用线性系统中得到成功应用的谱分析方法，希望把这种方法应用到非线性系统分析中来［3］。在预报船舶非线性横摇时，用线性化方程代替非线性方程，从而用谱分析的方法进行统计计算，其难点在于对非线性方程的线性化。

本文在线性横摇运动方程的基础上，运用能量法，对正横规则波中船舶非线性横摇运动方程进行等效线性化，并验证其工程实用性，为船舶横摇预报提供理论分析计算模型。

1 船舶在正横规则波中的线性横摇

目前，有多种研究船舶横摇的数学模型均可有效模拟横摇过程，但这些模型都以Mathieu方程为基础建立，即：

惯性力矩+阻尼力矩+恢复力矩=波浪扰动力矩

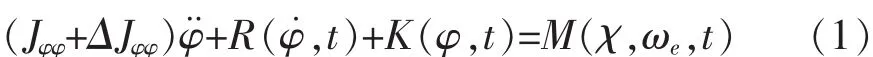
式中：Jφφ为船体自身转动惯量；

ΔJφφ为附加质量转动惯量；

φ为船舶横摇角；

R（φ，t）为横摇阻尼力矩；

K（φ，t）为横摇恢复力矩；

M（χ，ωe，t）为波浪扰动力矩。

假设船舶在正横规则波上作小角度横摇，则可认为阻尼力矩与横摇加速度成线性关系，恢复力矩与横摇角呈线性关系，并假设船宽与波长的比是小量。根据动平衡原理，船舶在正横规则波中横摇运动微分方程为

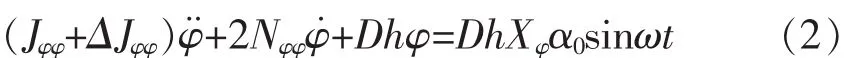
式中：2Nφφ为阻尼力矩系数；

D为船舶排水量；

h为船舶横稳心高；

Xφ为波面角修正系数；

α0为波面角振幅；

ω为波浪圆频率。

式中：XφT为考虑吃水有限性引起的动压力修正系数，它取决于吃水与波长比（T/λ）和船舶横剖面形状；

XφB是考虑船宽有限性的修正系数，它取决于船宽与波长比（B/λ）和船舶横剖面的形状。

式（2）两边同时除以（Jφφ+ΔJφφ），经整理得

式（4）为典型的二阶常系数非齐次线性微分方程，它的解应为齐次微分方程的通解加上该方程的一个特解。由于前面假定波浪是微幅平面简谐波，船本身是二阶线性系统，则该横摇运动也应是简谐运动，故令其特解为

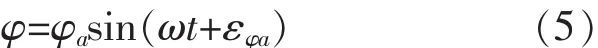
式中：φa为横摇幅值；

εφa为横摇角φ相对于波面角α的相位差。

将式（5）及其对时间t的一次及二次导数代入到式（4）中，得

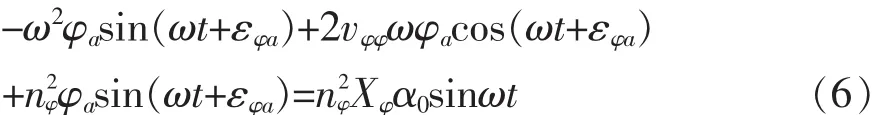
将式（6）等号左边项中括号展开，经整理得

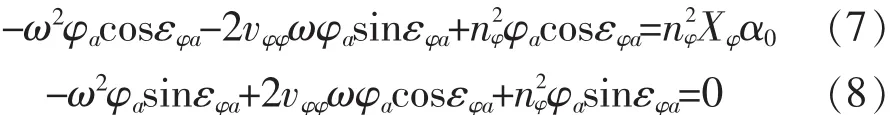
由式（8）得

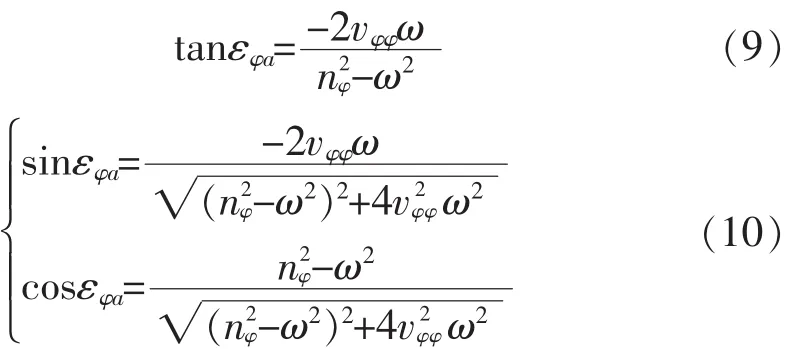
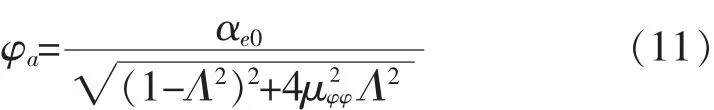
式中：αe0=α0Xφ，为有效波面角振幅；

将式（10）代入式（7），经整理得

当船的无因次衰减系数μφφ和有效波面角振幅αe0确定后，根据式（11）可计算船舶在正横规则波中的横摇幅值。

对式（11）进行变换，得

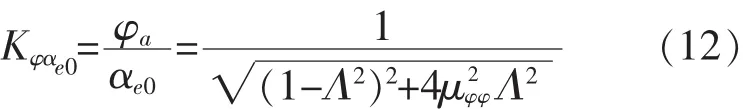
式中：Kφαe0称为横摇相对有效波面角的幅频响应函数或放大系数。

由式（9）可得相位差

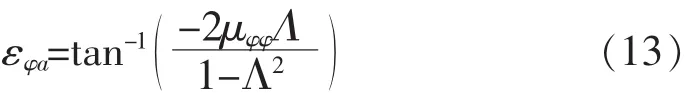
2 船舶在正横规则波中的非线性横摇的线性化

以上讨论船舶的横摇运动为微幅假设下的线性横摇，可以用二阶常系数线性微分方程描述，用普通的数学方法求解。实际上，船舶在大风浪里的摇荡运动并非微幅，尤其是船舶的大幅度横摇更为突出，它属于典型的非线性运动问题。

船舶大幅度横摇运动的非线性主要表现在恢复力矩的非线性、阻尼力矩的非线性及波浪扰动力矩的非线性三个方面。本文主要针对恢复力矩和阻尼力矩的非线性进行分析论述。

船舶在大风浪中航行时，一般横摇角都超过8°～10°，这时阻尼力矩不再随横摇角呈线性变化，而是呈非线性变化［4］。横摇非线性阻尼力矩有多种函数表达形式，本文采用线性阻尼加三次阻尼的一般阻尼形式，如式（14）所示：式中：Nφφ、W均为系数。一般认为该表达式适合中等横摇的情况。

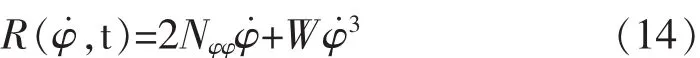
随着横摇角度的增加，恢复力矩与横摇角成非线性关系，其非线性由船舶的静稳性曲线的真实形状确定。通常中等横摇情况的恢复力矩非线性表达式为：

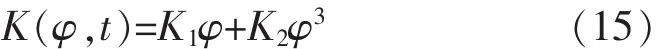
式中：K1、K2为通过拟合船舶静稳性曲线得到的系数。将式（14）和（15）代入到式（1）中，整理得：

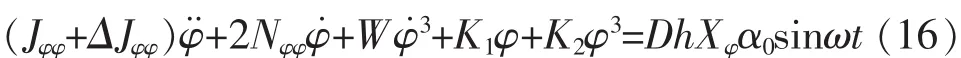
式（16）为一非线性方程，采用常规的数学方法很难得到其精确解。本文根据能量法将其等效线性化求其近似解，即等效为以下形式

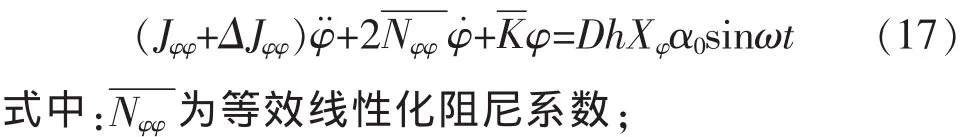
2.1 恢复力矩的线性化

设等效线性化后的方程（17）的一个特解为

将式（18）代入式（15），并将非线性项展开，得：

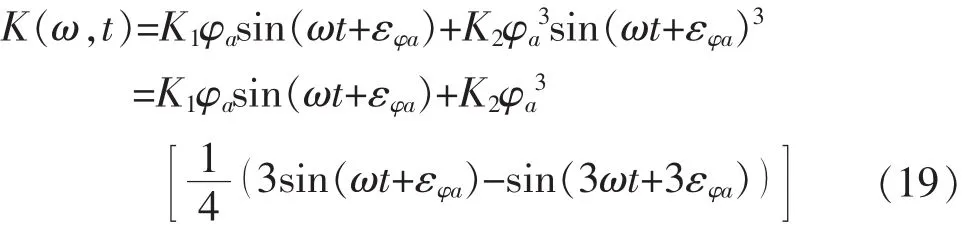
恢复力矩在一个摇荡周期里做的功为0，它只引起动能和势能等能量之间的转换，不耗散能量。因此，对恢复力矩的线性化即为直接展开非线性项，并略去高频项。

略去式（19）中的高频项并整理，得：

2.2 阻尼力矩的线性化

阻尼力矩不同于回复力矩，它要耗散船舶的运动能量。但无论采用哪种阻尼力矩的函数表达形式，

令 φ=φasint），采用式（14）中阻尼力矩的函数表达形式，在一个摇荡周期内所做的功为：在一个完整的横摇周期内所做的功都一样。

等效线性阻尼在一个摇荡周期内所做的功为：

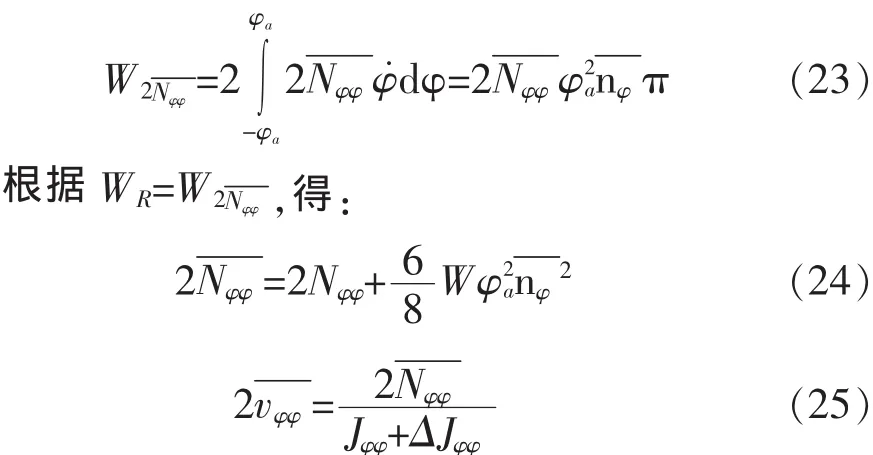
将方程式（17）两边同除以（Jφφ+ΔJφφ），整理得：

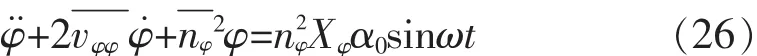
设式（26）的特解为 φ=φasin（ωt+εφa），由以前的推论可知：

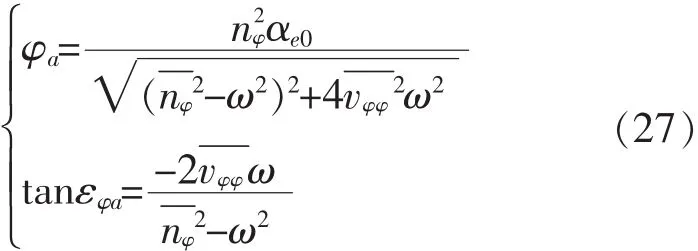
等效线性方程的解与线性方程的解不同处在于：等效线性方程的阻尼力矩系数和恢复力矩不再是常数，而是与待求的横摇角幅值有关。因此，应将式（26）与式（21）和式（25）联立迭代求解。

3 实例验证

在中等摇幅情况下，可认为恢复力矩仍为线性，此时阻尼力矩已呈现出非线性。本文以某型号船为例，验证阻尼为非线性时线性化后方程的实用性。该船基本参数见表 1［5］。

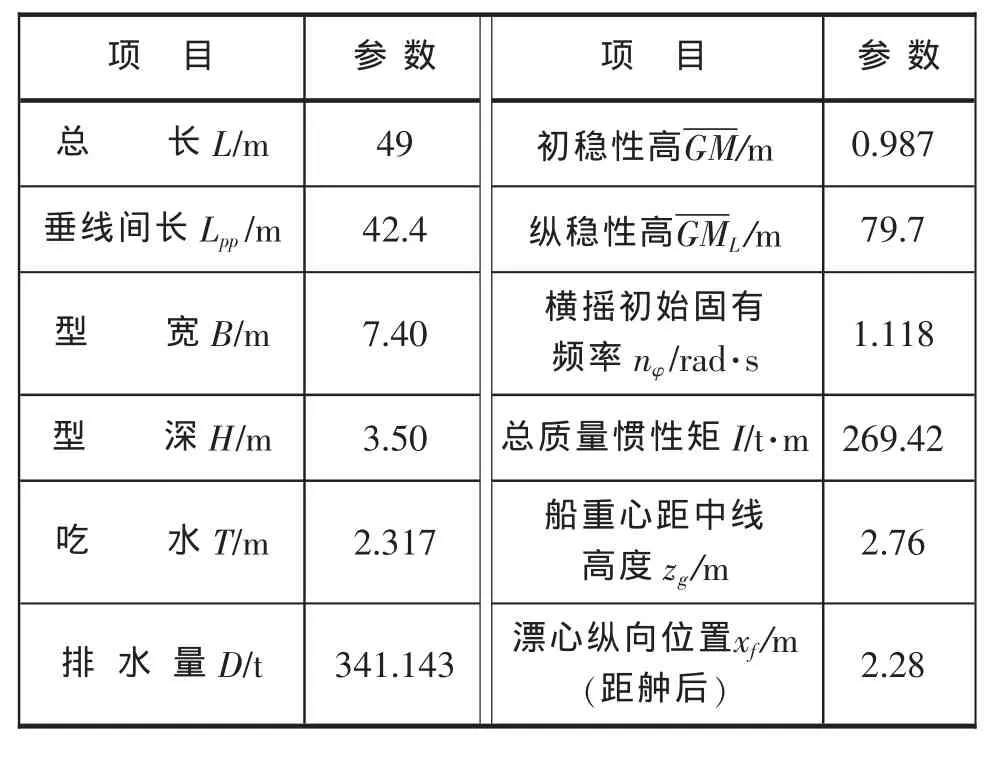
表1 船舶基本参数

根据经验公式可以得到线性横摇阻尼系数2N=18.75 tm2s-1，三次非线性横摇阻尼系数W=144.6 tm2s，与其对应的横摇衰减系数为2v=0.069 6 s-1，w=0.536 7 s。 取波长为 λ=40 m，波高为H=3 m，波浪频率ω==1.245 rad/s。波面角修正系数Xφ=0.823 2；波面角振幅α0=0.235 6。该船舶的非线性运动方程为：

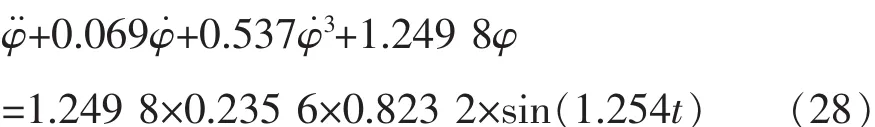
采用数值解法解此方程，可得其稳定横摇幅值

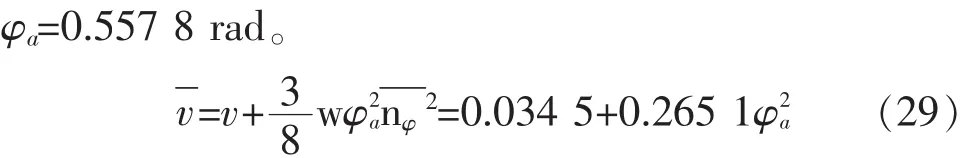
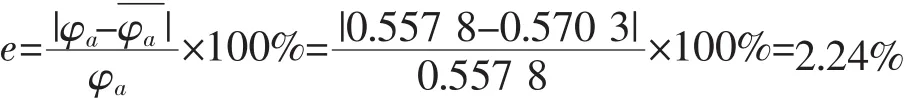
相对误差为2.24%，控制在工程应用可接受范围内，故该等效线性化模型可应用于实际工程分析计算。

根据以上计算结果可得摇幅相对误差：

4 结 语

近年来，有关非线性动力学理论研究取得的众多成果及迅速发展的计算机科学技术，极大地推动了船舶非线性问题的研究步伐，人们开始采用非线性动力学理论来研究船舶的大幅横摇运动及倾覆机理。线性系统中的谱分析法，作为一种古老而成熟的分析方法，在船舶运动预报中仍被广泛运用［6］。

本文基于能量法对规则波中船舶非线性横摇运动方程进行线性化，导出线性化系数表达式，经实例验证表明该线性化模型具有实际工程应用价值。得到线性化方程后，即可进一步得到该方程的频响函数。当输入量波浪扰动力（矩）已知时，即可方便地求得对应的船舶摇荡运动的幅值和相位角，极大简化了预报程序。

［1］A.H.Nayfeh.On the undesirable roll characteristics of ship in regular seas［J］.Journal of Ship Research，1988，32（2）：95～100.

［2］冯铁成.船舶摇摆与操纵［M］.北京：国防工业出版社，1980.

［3］李积德.船舶耐波性［M］.哈尔滨：哈尔滨工程大学出版社，2007.

［4］邝艳香.纵浪中船舶参数激励非线性随机横摇研究［D］.天津：天津大学，2008.

［5］李红霞.纵浪和斜浪中船舶非线性运动特性研究［D］.天津：天津大学，2007.

［6］Jianbo Hua.A Study of The Parametrically Exceited Roll Motion of A RoRo-Ship in Following and Heading Waves［J］.Int.Shipbuild.Progr.，1992，39（420）：345～366.