软辫线对屏蔽电缆耦合的影响分析与仿真＊

张兰芳

（湖北水利水电职业技术学院 武汉 430070）

1 引言

随着电气电子设备向集成化综合化发展，电缆耦合所带来的电磁兼容问题日益突出［1～2］。特别是弱信号类线缆，不仅种类繁多、数量大，而且其敷设走向错综复杂，很容易在周围其它电力电缆以及较大强度信号电缆作用下，借助空间场的耦合拾取不必要的电磁能量，从而影响信息传输质量，甚至发生意外事故。在实际的电缆敷设时，屏蔽层的接地需要使用软辫线的方式将屏蔽层与连接器的管脚相连，这些被暴露的软辫线部分往往会引入电磁耦合。如何降低电缆因屏蔽层采用软辫线接地而带来的干扰风险，其途径就是通过仿真计算来准确预测软辫线对屏蔽电缆耦合的影响，以便及时判断潜在问题区域。以往的研究模型主要集中在非屏蔽电缆，如C.R.Paul、Levin B.M、Pignari S等研究了非屏蔽的多导体传输线电缆间串扰的频域响应［3～6］，Bellan等分析计算了非均匀电缆束的耦合影响［7］。关于软辫线对屏蔽电缆耦合引起的串扰响应研究则涉及甚少。

本文针对工程中的电缆耦合问题，运用三导体传输线的理论分析了屏蔽层采用软辫线接地情况下的屏蔽电缆受邻近电缆耦合引起的串扰。在此基础上，仿真分析了因电缆间耦合作用到软辫线上而在屏蔽电缆上引起的串扰电压的幅频响应特征，结果表明：软辫线一定程度上降低了屏蔽线的屏蔽效能，所产生的耦合干扰要大于屏蔽层3600环接时的耦合干扰。

2 软辫线影响分析

考虑如图1所示的三导体传输线等效电路。其中的参考导线（地线）是其它所有导线中的电流的返回线。

图1 接收电缆屏蔽时的三导体传输线横截面结构

发射导线和接收导线具有每单位长度的电阻rG和rR。hG是发射导线距地面的高度，hR为接收导线距地面的高度，rwG为发射导线的半径，rwR为接收导线的芯线半径，rsh是屏蔽层内径。根据电磁感应耦合的基本原理可知，两线间的互电感会产生磁场耦合，该耦合作用在屏蔽电缆上会对其上的电流、电压造成一定影响［8～9］。而两线间的互电容会产生电场耦合，该耦合作用在屏蔽电缆上会对其上的电流、电压造成一定影响［10～11］。

设定US为源电压，RS为源阻抗，RL为负载，RNE为接收导线近端终端负载，RFE为接收导线远端终端负载。则近端与远端的感性串扰电压分别为：

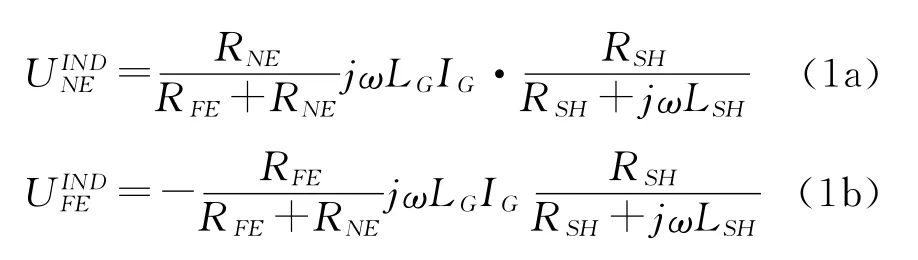
屏蔽层的拐点频率为

其中，屏蔽层总电阻为RSH＝rSτ，屏蔽层－接地平面回路的总自电感为LSH＝lSτ。

于是近端与远端的容性串扰电压分别为

进一步，对容性耦合与感性耦合进行分析如下：

当频率低于拐点频率fSH时，SF＝1，屏蔽层两端接地也不会影响到感性耦合。而当频率高于拐

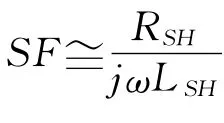
在实际的电缆敷设时，屏蔽层的接地需要使用软辫线的方式将屏蔽层与连接器的管脚相连。对于电短传输线，其终端串扰则是在非屏蔽导线间串扰的基础上叠加两段软辫线部分的串扰以及屏蔽层部分的串扰，即：

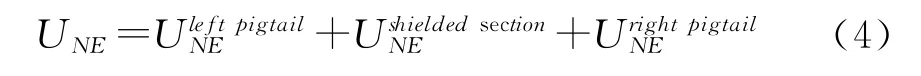
其中的每一个分量都是容性耦合与感性耦合分量之和。

综合上述分析，如果屏蔽层至少一端接地，那么容性耦合将为零。只有当屏蔽层两端都接地且频率大于屏蔽层的拐点频率，即f＞fSH时，感性耦合才会受到屏蔽层的影响，此时串扰为常数，与频率无关。事实上，由于终端屏蔽层“软辫线”的影响，当频率往上增加的同时串扰也会开始增加。

3 仿真分析

通过设计发射导线对带软辫线的接收导线的电磁耦合数值仿真系统，考察屏蔽层两端接地时因软辫线作用所带来的串扰影响。

仿真中设置发射导线长1m，终端电阻50Ω；接收导线屏蔽层两端接地。为考察接收导线软辫线的长度对耦合情况的影响，分别设定接收导线两端的软辫线长度为2cm，4cm以及8cm，三种情况下近端耦合的结果如图2所示。

图2 软辫线的长度对耦合情况的影响

可以看到，软辫线越长，所带来的耦合干扰就越大。在屏蔽层拐点频率以上，由于屏蔽线部分的耦合曲线变平，而软辫线的耦合继续以20dB／10倍频的速度增加，并逐渐超过屏蔽线部分的耦合，于是耦合干扰继续增加，并呈现一定震荡现象。

由此而言，软辫线的存在降低了屏蔽线的屏蔽效能，屏蔽层通过软辫线连接后所产生的耦合干扰要大于屏蔽层3600环接时的耦合干扰。软辫线越长，则耦合程度就越大。除非在屏蔽线两端都进行3600环接，才能保证屏蔽线的良好性能。

4 结语

如何降低电缆因屏蔽层采用软辫线接地而带来的干扰风险，其途径就是通过仿真计算来准确预测软辫线对屏蔽电缆耦合的影响。本文着重探讨了软辫线对屏蔽电缆耦合的影响，分析了屏蔽层采用软辫线接地情况下的屏蔽电缆受邻近电缆耦合引起的串扰。仿真结果表明：软辫线的存在一定程度上降低了屏蔽线的屏蔽效能。只有在屏蔽线两端都进行3600环接，才能保证屏蔽线的良好性能。

［1］毕季明，黄小华.海军舰船电磁兼容控制技术与措施［J］.舰船电子工程，2007，27（2）：201～203

［2］Kodali V Prasad.Engineering Electromagnetic Compatibility［M］.IEEE Press，1996

［3］Levin B.M.Calculation of Crosstalks in Multiple-Conductor Cables［C］／／Proceeding of DIPED'07，2007：211～214

［4］Paul C.R.Analysis of Multiconductor Transmission Lines［M］.New York：John Wiley Interscience，1994

［5］Pignari S，Canavero F.G.A Transmission Line Simulator for EMC in Complex Electronic Systems［J］.International Journal of Numerical Modelling：Electronic Networks，Devices and Fields，1997（10）：13～34

［6］Clayton R.Paul.Solution of the Transmission-Line E-quations Under the Weak-Coupling Assumption［J］.IEEE Transactions on Electromagnetic Compatibility，2002，44（3）：413～423

［7］Bellan D，Pignari S.A.Estimation of Crosstalk in Nonuniform Cable Bundles［C］／／Proc.2005IEEE Int.Symp.on Electromagn.Compat，Chicago，IL，USA，Aug.8-12，2005：336～341

［8］陈穷，等.电磁兼容性工程设计手册［M］.北京：国防工业出版社，1993

［9］Savage J.S，Smith W.T.Capacitance Calculations for Cable Harnesses using the Method of Moments［J］.IEEE Transactions on Electromagnetic Compatibility，1995，37（1）：131～137

［10］Gavrilakis A.，Al-Asadi M.M.，Duffy A.P.Method for Prediction of Capacitance of Shielded Transmission Lines［J］.IEEE Electronics Letters，2001，37（23）：1424～1425

［11］Sadiku M.N.O.Numerical Techniques in Electromagnetics［M］.Boca Raton，FL：CRC Press，1992