基于FuzzyPID的UUV姿态控制器研究＊-

周冉辉 万 立

（华中科技大学机械科学与工程学院 武汉 430074）

1 引言

UUV（无人水下航行器）在航行过程中，随着航行速度、航行高度、UUV质心及压力中心等因素的变化以及外部环境的影响，UUV的航行动力学特性也会发生较大的变化，呈现严重的非线性，特别是对于新型的反舰UUV，传统的PID控制难以满足控制要求［1］，很难保证UUV在大海域和快速机动的情况下仍有足够的稳定性和精度。因此UUV控制系统的设计要求控制规律具有较强的鲁棒性。设计一种鲁棒性强的控制器对于参数变化剧烈的被控对象是很有通用性的。

Fuzzy-PID控制器是一种智能控制器，它根据人工控制规则组织控制决策表，然后采用模糊推理的方法实现PID参数实时自整定，不仅保持了常规PID控制系统原理简单、使用方便、鲁棒性较强、控制精度高等优点，而且具有模糊控制的灵活性、适应性强等优点，特别适合于那些难以建立精确数学模型、非线性、参数变化范围大和大滞后过程的控制系统。因此将模糊控制用于UUV控制系统的设计是很合适的。

本文设计了一种Fuzzy-PID姿态控制器，它可以根据系统输出对PID控制器参数进行实时修正，并结合Matlab的Simulink对其进行仿真分析。

2 UUV纵向运动数学模型

实践证明，通过对UUV运动的解耦可以实现UUV控制系统三个通道的独立设计。现以UUV俯仰通道为例，从UUV的受力分析、力矩平衡入手列写微分方程。若仅考虑雷体的姿态变化，忽略速度变化的影响和次要因素，采用小扰动法理论，则可以得到UUV纵向运动方程的最简形式如下［2］：

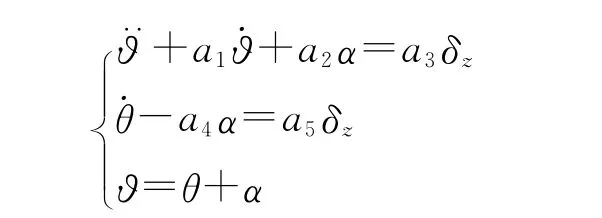
式中ϑ、θ、α、δz分别表示 UUV的俯仰角、弹道倾角、攻角、升降舵偏转角；a1～a5为UUV动力学系数。对上式进行拉氏变换便可得UUV纵向传递函数的标准形式：

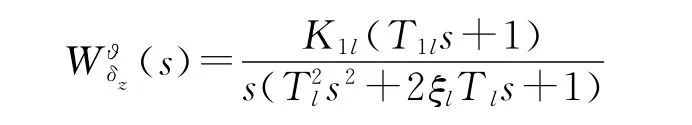
式中K1l表示单位舵角作用下产生的弹道倾角速度；Tl表示UUV攻角跟踪舵偏角的快慢程度；T1l表示弹道倾角相对于UUV姿态角所具有的惯性；ξl表示UUV的阻尼系数。

3 UUV纵向姿态控制器设计

3.1 Fuzzy-PID控制原理

运用模糊数学的基本理论方法，把规则的条件、操作用模糊集表示，并把这些模糊控制规则以及有关信息（如评价指标、初始PID参数等）作为知识存入知识库中，然后再根据控制系统的实际响应情况（即专家系统的输入条件），运用模糊推理，即可自动实现对PID参数的最佳调整，这就是Fuzzy－PID控制。Fuzzy-PID控制器目前有多种结构形式，但其工作原理基本一致。

图1 Fuzzy-PID控制结构图

图2 隶属度函数曲线

由图1看到，Fuzzy-PID控制由常规PID控制部分和模糊推理两部分组成，模糊推理部分实质就是一个模糊控制器，只不过它的输入是偏差e和偏差变化率ec，输出是ΔKp，ΔKi，ΔKd。PID参数模糊自整定是找出PID的三个参数和偏差e和偏差变化率ec之间的模糊关系，在运行中通过不断检测e和ec，根据模糊控制原理来对三个参数进行在线修改，以满足不同e和ec时对控制参数的不同要求，而使被控对象有良好的动、静性能。

3.2 UUV纵向Fuzzy-PID控制器设计

在设计中，应当保持模糊推理系统的输入输出变化范围，推理结果可由量化因子（K1，K2，γp，γi，γd）来修正。为简单起见，这里将模糊推理系统的输入（两个）以及输出（三个）的变化范围定义为模糊集上的论域：（输入变量，输出变量）＝｛－3，－2，－1，0，1，2，3｝；其模糊子集为：（输入变量，输出变量）＝｛NB NM NS ZE PS PM PB｝。考虑到对论域的覆盖程度和灵敏度、稳定性与鲁棒性原则，各模糊子集采用三角形隶属函数。关于量化因子以及隶属度函数的确定原则参见文献［3］。

模糊控制器的核心是“IF…THEN…”形式的模糊控制规则，控制规则的选取直接关系到系统控制性能的优劣，是设计的关键。参见PID控制中Kp、Ki、Kd的作用［4］：

1）比例增益Kp增大，可以加快响应速度，减小系统稳态误差，提高控制精度，但是过大会使系统产生超调，甚至导致不稳定；

2）积分作用主要是消除系统静态误差，加强积分作用，有利于减小系统静差，但是Ki过大，会加大超调，甚至引起振荡；

3）微分作用可以改善动态性能，增大微分增益Kd，有利于加快系统响应，使系统超调量减小，稳定性增加，但对扰动敏感，抑制外扰能力减弱。若Kd过大，会使调节过程出现超调减速，调节时间增长；反之，若Kd过小，系统响应变慢，稳定性变差。

图3 Fuzzy-PID控制器3个参数的模糊推理规则曲面

根据上述分析同时考虑到三个参数之间的相互影响，本文参考文献［5］采用如表1所示的模糊控制规则。在Matlab提供的模糊推理系统编辑界面中输入以上信息可以完成模糊推理系统的编辑。其中图2是隶属度函数曲线，图3是Fuzzy-PID控制器3个参数的模糊推理规则曲面。

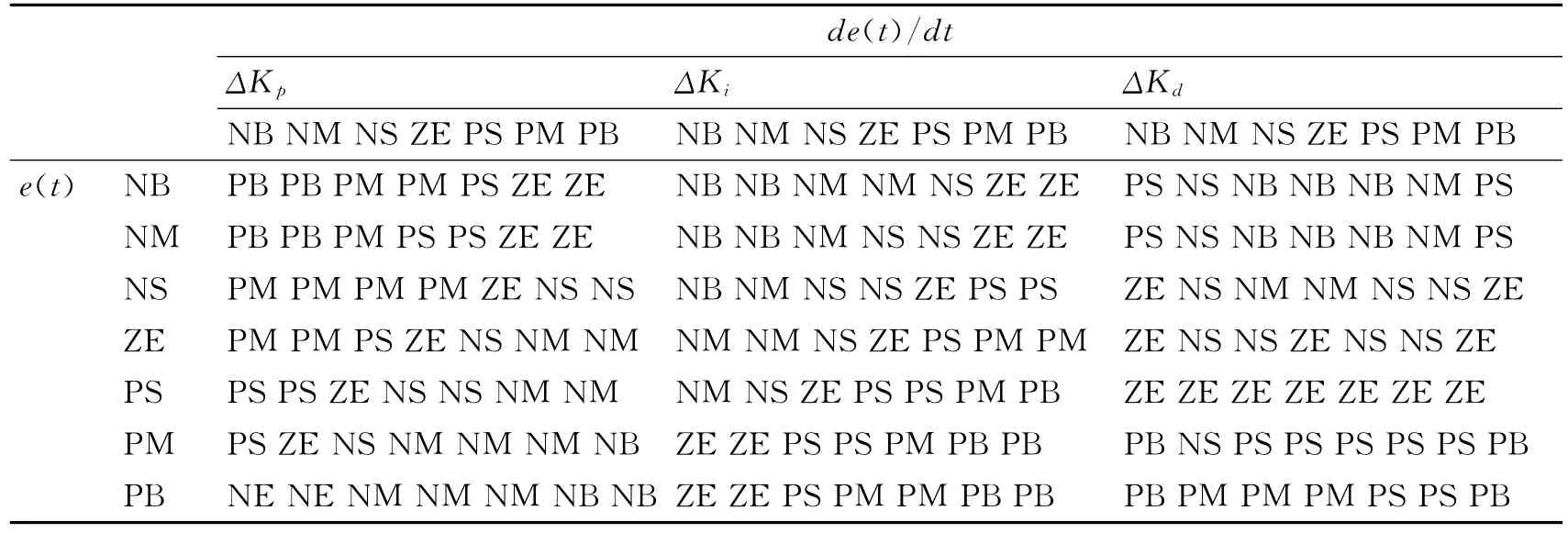
表1 模糊控制规则

4 仿真及结果分析

以UUV纵向运动模型为被控对象，分别采用Fuzzy-PID控制器和PID控制器对控制系统进行仿真。在UUV运动的某特征点分别取K1l、T1l、T1、ξl的值［2］为0.91、1.634、0.184、0.091；采用定步长、ode23求解器求解，采样周期Ts＝0.05s；取单位阶跃信号为输入信号。仿真中取PID控制器参数：Kp＝3，Ki＝1，Kd＝2；取Fuzzy-PID控制器参数：Kp0＝3，Ki0＝1，Kd0＝2，K1＝3，K2＝3，γp＝3，γp＝1.6，γi＝1，γd＝1.2。仿真结果见图4、图5所示。从图中可以看到，Fuzzy-PID控制较PID控制超调量小、调节时间短，效果较好；当响应趋于稳态时，Kp，Ki，Kd也趋于各自的稳态值。

图4 阶跃输入如下的仿真比较

图5 Fuzzy-PID的三个参数变化趋势

5 结语

针对UUV航行过程系统参数不确定性和变化较大的情况，设计了一种模糊PID控制器。模糊PID控制算法充分利用了模糊控制和PID控制的优点，可以在线自调整PID的参数。数学仿真表明，将此控制器用于UUV的俯仰通道姿态稳定的控制中具有较强的鲁棒特性，起到良好的控制效果。但在设计中发现为了达到理想的控制效果，需要反复调整Fuzzy-PID控制器的初始参数以及量化因子，另外输入、输出的隶属度函数和模糊控制规则对控制效果也有较大影响。所以，Fuzzy-PID控制器的参数调整是控制器设计的难点，同时这也是控制器达到优良性能的保障。

［1］张前进.基于Fuzzy-PID的导弹控制系统设计研究［J］.弹箭与制导学报，2003，23（3）：10～11

［2］潘荣霖.飞航导弹自动控制系统［M］.北京：中国宇航出版社，1991：110

［3］常晓恒.模糊自整定PID控制器的设计［D］.辽宁：辽宁工程技术大学，2004

［4］何克忠，李伟.计算机控制系统［M］.北京：清华大学出版社，1998：50

［5］薛定宇.控制系统计算机辅助设计—MATLAB语言与应用［M］.北京：清华大学出版社，2006：67

［6］诸静.模糊控制原理与应用［M］.北京：机械工业出版社，1995：167

［7］黄景全，张宇文.鱼雷流体力学［M］.西安：西北工业大学出版社，1989：80

［8］涂德民.鱼雷控制系统计算机辅助分析设计与仿真—高等学校教材［M］.西安：西北工业大学出版社，2000：155

［9］刘伟东，刘刚，林轶群，等.网络化鱼雷控制系统仿真［J］.计算机测量与控制，2008，16（11）：1647

［10］吕强，郭善亮，王冬来，等.基于DSP四旋翼飞行器姿态控制系统硬件设计［J］.计算机与数字工程，2011，39（7）

［11］王建辉.自动控制原理［M］.北京：清华大学出版社，2007：444