基于航迹信息的舰船姿态角估计研究＊

应 涛 章力强 李相平

（海军航空工程学院电子信息工程系 烟台 264001）

1 引言

一部雷达如果有足够高的距离分辨力，那么它就能分辨出一个目标中不同的散射中心，而且能给出目标的一维距离像。如果这部雷达的方位分辨力也足够高的话，那么就能对目标进行二维成像，给出目标的SAR或ISAR图像。雷达目标的一维距离像、SAR像和ISAR像对目标的姿态角非常敏感，即同一目标的姿态角很小的变化就能引起其一维距离像、SAR像和ISAR像较大的变化。因此，在利用目标的一维距离像、SAR像或ISAR像作为目标特征信号来进行目标识别时，为了能够很好地利用模板库中的模板进行目标识别，需要对未知目标的姿态角进行估计，而观察目标的航迹是估计目标姿态角的一种方法［1］。

精确估计出舰船目标的姿态角是基于一维距离像、SAR像和ISAR像海上舰船目标识别的一项关键技术，能够大大缩小识别算法的搜索空间，舰船运动的姿态角估计对于自动目标测长［2～3］和雷达目标识别具有重要意义［4～5］。本文针对舰船目标运动特点提出了一种基于航迹信息的舰船姿态角估计方法，该方法首先建立舰船目标运动模型，然后采用基于Singer模型的自适应跟踪算法对舰船目标进行滤波跟踪，最后对舰船目标航迹进行多项式拟合，优化目标数据，从而准确地估计出舰船姿态角，而仿真结果表明了该方法的有效性和稳定性。

2 舰船目标航迹估计

2.1 舰船目标运动模型

由于在短时间内舰船运动可以看作一个平面运动，舰船目标的雷达坐标（距离R和方位角A）可通过雷达跟踪测量获得，如图1所示。以雷达测站为原点建立直角坐标系：

图1 直角坐标系中的舰船运动轨迹示意图

对测量数据进行逐段拟合，在短时间（几个至几十个测量周期）内，目标在x、y轴上的运动特性可用时间的二次项来描述［6］：

式中T是起始时间。

2.2 基于Singer模型的滤波跟踪算法

变维滤波算法、输入估计算法等算法是把机动控制项作为白噪声建模，白噪声模型是一种比较理想化的模型，其实更切合实际的机动模型是把机动控制项作为相关噪声（有色噪声）建模。1970年R.A.Singer提出的Singer模型法认为机动模型是相关噪声模型，而不是通常假设的白噪声模型［7］而对目标加速度a（t）作为具有指数自相关的零均值随机过程建模，即

式中，σ2m、α是在区间［t，t＋τ］内决定目标机动特性的待定参数；σ2m是目标的加速度方差；α是机动时间常数的倒数，即机动频率，通常α的经验取值范围为：目标机动形势是飞机慢速转弯，1／α的取值为60s，对于逃避机动是20s，大气扰动是1s，它的确切值要通过实时测量才能确定。

对于机动加速度方差σ2m，我们可以根据机动目标的概率密度函数来计算。通常对机动加速度的分布作如下假定：1）机动加速度等于极大值aM的概率为pM，等于－aM的概率也为pM；2）机动加速度等于0的概率为p0（非机动概率）；3）机动加速度在区间［－aM，aM］上近似服从均匀分布。由以上假设可得如下的概率密度函数［8］：

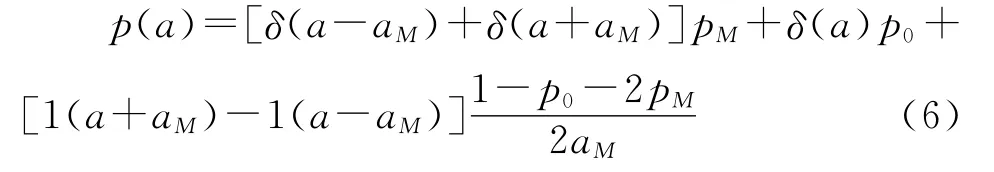
式中，1（·）是单位阶跃函数；δ（·）是狄拉克脉冲函数。

由上述概率密度函数可得与式（6）对以后能够的方差为

对式（5）的时间相关函数R（τ）进行白化处理之后，可用输入为白噪声的一阶时间相关模型表示为（该动态模型是一阶马尔可夫过程）

式中，～v（t）是均值为0、方差为2ασ2m的高斯白噪声，即

令关于坐标x的状态向量为

式中，x..＝a，上述一阶时间相关模型如果用状态方程可表示为

这就是著名的Singer模型，其中系统矩阵

过程噪声

将A和～V代入式（11）有

对于采样间隔T，与式（11）对应的离散时间动态方程为

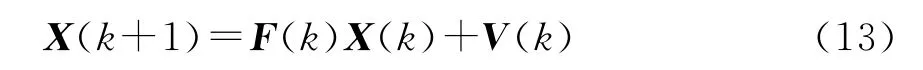
式中

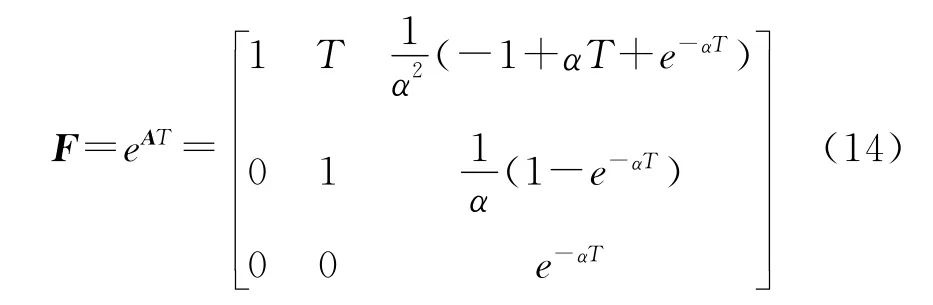
其离散时间过程噪声V具有协方差

式中假定αT≪1，即采样间隔T比机动自相关时间常数1／α小得多。在雷达对目标的跟踪中，如果更新率足够高，则认为上述假定（αT≪1）是正确的。但在远距离声纳（主动声纳和被动声纳）对目标的跟踪中，则相反情况是真实的，即αT≫1。量测方程和卡尔曼滤波方程和白噪声建模类似，只不过量测矩阵H可能会有所不同，这里H为

式中，Q的精确表达式为（Q为对称阵）：

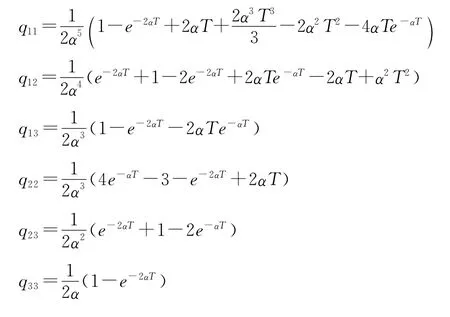
3 姿态角估计

3.1 最小二乘拟合

雷达测得目标航迹（xi，yi）（i＝1，2，…，m），对于曲线y＝φ（x），一般情况下，我们不能要求近似曲线y＝φ（x）严格地通过所有数据点（xi，yi），亦即不能要求拟合函数在xi处的偏差（亦称残差）δi＝φ（xi）－yi，i＝1，2，…，m都严格地等于零。为了便于计算、分析与应用，我们较多地根据“使偏差平方和最小”的原则（称为最小二乘原则）［9］来选择拟合曲线y＝φ（x）。

考虑m次多项式

系数a0，a1，…，am应该满足如下计算系数方程组

图2 目标真实航迹、量测值和滤波值对比图

其中j＝0，1，2，…，m。上式方程组的系数矩阵是一个对称矩阵，是正定的。可以唯一解出系数a0，a1，a2，…，am，然后代入m次多项式（17），即可得到由观测数据点（xi，yi）（i＝1，2，…，n）所确定的近似多项式。

方程组（18）中的m＋1个方程通常称为法方程，可证明此方程组的系数行列式不可能为零，因此它有唯一解。

3.2 舰船目标姿态角估计

在不考虑横摇和纵摇的情况下，假设舰船目标是轴对称的，则目标的姿态角估计可以简化成雷达观测方向与目标运动方向的夹角，如图1中的角θ。

由式（3）和（4）可知，在各个时刻，目标在x和y方向的速度分别为

那么，在t时刻，目标的姿态估计角为［10］

4 仿真结果与分析

为验证上述方法的有效性，现设计仿真实验，并对仿真结果进行分析。设一舰船目标在x轴上做匀速运动，在y轴上做匀加速运动，x轴上的初始位置和初始速度分别为4000m和20m／s，y轴上的初始位置、初始速度和加速度分别为8000m、－8m／s和－0.08m／s2，雷达扫描周期T＝2s，将雷达的真实轨迹加上一个高斯噪声当作是雷达的量测数据，然后采用Singer模型跟踪滤波，并对舰船目标航迹采用5阶多项式拟合，得到的仿真结果如图2、3和图4所示。

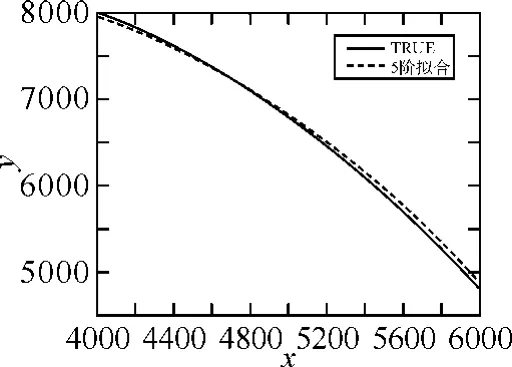
图3 目标真实航迹和5阶拟合航迹对比图

图4 5阶拟合与Singer滤波结果对比图

由图2～4可以看出，目标的真实航迹能够被很好地拟合，这是目标的姿态角能够被有效估计的前提。目标航迹数据经过基于Singer模型的滤波跟踪和5阶航迹拟合之后，5阶拟合结果的绝对误差明显要比基于Singer模型滤波结果的绝对误差要小得多，这是由于经过Singer模型出来的数据在经过5阶拟合处理就可以看作是再经过一次最小二乘滤波，使数据进一步优化，这是有利于接下来精确地估计目标姿态角的。当对舰船目标航迹进行2阶、5阶、7阶和10阶拟合时得到的拟合残差如图5所示。

图5 2阶、5阶、7阶和10阶拟合的残差对比

从图5中不难看出，5、7、10阶拟合效果要明显好于2阶拟合的效果，而5阶拟合效果与7阶和10阶差不多，也并不是拟合阶数越高越好。为了兼顾运算量和精度，在这里采用5阶拟合。

在对舰船目标进行航迹拟合之后，就要进行姿态角估计，采用上述方法进行姿态角估计得到的仿真结果如图6、7所示。在对舰船目标航迹数据进行Singer滤波之后，若定义

为舰船目标运动的速度。其中为舰船目标的位置，T为观测周期。直接用此数据来进行目标姿态角估计得到的结果如图8所示。显然，图8中反映的目标机动性与真实不符。而从图6、7不难看出，用该方法估计的姿态角与目标真实姿态角十分接近，最大误差不超过5度，因此，该方法能够准确、有效地估计舰船目标的姿态角。

图6 姿态角估计值与真实姿态角对比图

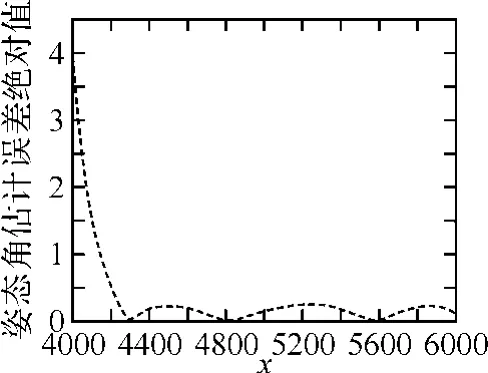
图7 姿态角估计绝对误差

图8 Singer模型数据姿态角估计

5 结语

姿态角是舰船目标的一个重要特征量，利用上述方法能够稳定、有效地估计出目标姿态角。对于基于高分辨距离像、ISAR像的目标识别来说，精确地估计出其姿态角能够大大缩小目标识别算法的搜索空间，从而能够实现对舰船目标快速而正确地识别。但本文的方法没有考虑到在高海情下舰船的横摇和纵摇情况，也没有对如何进一步提高航迹拟合的精度做深入研究，因此下一步工作中将在这两个方面加以改进。

［1］Merrill l.Skolnik.Introduction to Radar System，third edition［M］.Publishing House of Electronics Industry，2006：277～278

［2］王涛，李士国，王秀春.一种基于高分辨距离像的目标长度特征提取算法［J］.中国电子科学研究院学报，2006，1（6）：532～535

［3］Frank E，Mc Fadden.Optimizing ship length estimates from ISAR in ages［C］／／IEEE，2000：163～168

［4］闫锦，黄培康.高距离分辨像雷达目标识别［J］.航天电子对抗，2004（2）：36～41

［5］Slamak S，Gibbins D，Gray D，et al.Features for high resolution radar range profile based on ship classification［R］.Fifth Intemational Symposium on Signal Processing and its Applications，1999：329～332

［6］李玉书.雷达目标散射截面动态测量方法研究［D］.南京：南京理工大学硕士论文，2002

［7］Y.Bar-Shalom，T.E.Fortmann.Tracking and Data Association.Academic Press，1988

［8］何友，修剑娟，张晶炜，等.雷达数据处理及应用［M］.第二版.北京：电子工业出版社，2009：154～158

［9］易大义，沈云宝，李有法.计算方法［M］.杭州：浙江大学出版社，1998

［10］刘先康，高梅国，傅雄军.空间姿态角估计与RCS反射图生成［J］.航空电子对抗，2006，23（1）：16～17