基于滑模观测器的永磁同步电机无传感器矢量控制*
2011-06-02范洪伟章跃进
孙 杰, 崔 巍, 范洪伟, 章跃进
(上海大学,上海 200072)
0 引言
永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)具有体积小、质量轻、功率因数高、效率高等优点,被广泛应用于各个领域。在PMSM控制技术中,矢量控制采用矢量变换的方法,将PMSM的磁通与转矩控制解耦,使其控制等效于直流电机,提高了PMSM的控制性能。
由于在PMSM矢量控制系统中,至关重要的一点是转子位置的获取,若获取的转子位置不精确,将会导致控制性能变差,影响电机的稳定运行。常用的位置检测器件如旋转变压器、光电编码器等。这些器件虽能精确地检测到电机的转子位置,但同时也增加了控制系统的成本,降低了系统的可靠性。为了解决由机械传感器带来的不便,无传感器技术应运而生。当前,无传感器技术大致可分为:基于电机模型的估算方法、基于模型参考自适应方法、高频注入估算方法、基于观测器估算方法和人工智能理论估算方法[1-7]。
滑模变结构控制是变结构控制系统的一种控制策略,该控制策略可以在动态过程中,根据系统当前的状态有目的的不断变化,迫使系统按照预定“滑动模态”的状态轨迹运动。PMSM是一个强耦合、非线性系统,将滑模变结构控制应用于电机控制系统中,能大大提高电机的抗参数摄动和外界扰动能力。由于滑模变结构控制在本质上的不连续开关特性,使得其会引起系统的抖振。抖振问题不仅影响控制的精度,增加能量消耗,严重时将会引起系统振荡或失稳[8]。本文将滑模变结构控制应用于PMSM矢量控制系统中,通过滑模观测器(Sliding Mode Observer,SMO)估算出电机的转子位置,并采用边界层法来削弱滑模控制的抖振问题。最后用仿真和试验的方法验证了该方案的正确性和有效性。
1 基于SMO的PMSM数学模型
PMSM的αβ坐标系下的数学模型如下[9]:

式中:eα,eβ——α,β 轴的反电动势,eα= - ωsin θ,eβ= ωcos θ;
iα、iβ,Uα、Uβ——α,β 轴的电流和电压;
R,L,Ke——电机的相电阻,相电感和反电动势系数。
根据PMSM在αβ坐标系下的数学模型,可构造如下SMO:


k——滑模系数;
Zα,Zβ——开关信号,其包含了反电动势的信息,可以通过一个低通滤波器对开关信号进行滤波,得到电机的反电动势。

通过式(6)、(7)得到转子位置角和转速的估算值:

由于反电动势是通过低通滤波器滤波得来,因此估算出的转子位置在相位上会有滞后,并且相位的滞后会随着电机转速的上升而变大。为了解决该问题,需要对估算的转子位置角进行相位补偿:
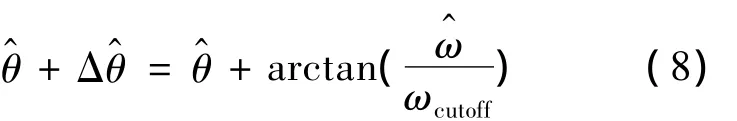
式中:ωcutoff——低通滤波器的截止频率。
图1为用SMO法估算转子位置的示意图。

图1 转子位置角估算框图
2 SMO中抖振的削弱
在理想情况下,当系统稳定时,将会严格地沿着滑模面进行滑动,但在实际系统中,由于时间滞后开关、空间滞后开关、系统惯性、系统延迟等因素,使变结构控制在滑动模态下伴随着高频抖振。抖振问题不仅影响控制的精度、增加能量消耗,严重时将会引起系统振荡或失稳。
本文在所构造的滑模控制器基础上引入了边界层的设计思想。边界层法实质上是准滑动模态控制方法的一种,准滑动模态控制是指系统的运行轨迹被限制在理想滑动模态的某一δ领域内,与理想的滑模控制相比,准滑动模态控制是使一定范围内的状态点被吸引至切换面的某一δ领域,而理想滑模控制则是使一定范围内的状态点都被吸引至切换面。准滑动模态不要求满足滑动模态的存在条件,因此准滑动模态不要求在滑动模态上进行结构变换的切换。边界层法采用饱和函数代替控制律中的切换函数,使控制作用在边界层内是连续控制,在边界层外是切换控制,从而削弱了在滑模面上的抖振现象。式(9)和图2分别为饱和函数的数学表达式和数学示意图。

图2 饱和函数示意图

式中,-δ~δ为边界层的厚度;γ=arctan(δ/k)为接近角。接近角过小,即δ过小,可能会由于控制量过大或控制器件惯性的存在,使得系统仍旧有抖振存在;接近角过大,即δ过大,虽然能够削弱滑模控制的抖振,但此时系统稳态精度降低,鲁棒性也下降。因此,接近角大小需要根据实际系统反复调试而得。
3 仿真与试验结果
本文在Simulink/MATLAB平台上进行仿真,仿真时所采用的PMSM参数如下:Rs=0.09 Ω,Ld=0.233 mH,Lq=0.302 mH,P=5。图3为根据前文所给的滑模算法搭建的仿真模块。

图3 滑模算法仿真模块
仿真时电机频率为50 Hz。采用边界层法时,接近角取为18°。图4(a)、(b)分别为引入边界层前后的反电势估算值。图5至上而下分别为电机的实际转子位置角、引入边界层前后的SMO估算角。从中可以发现,未引入边界层时,估算的反电势存在抖振,估算的电机转子位置角有抖动现象,而引入边界层后,估算的反电势和电机位置角都较为平滑。

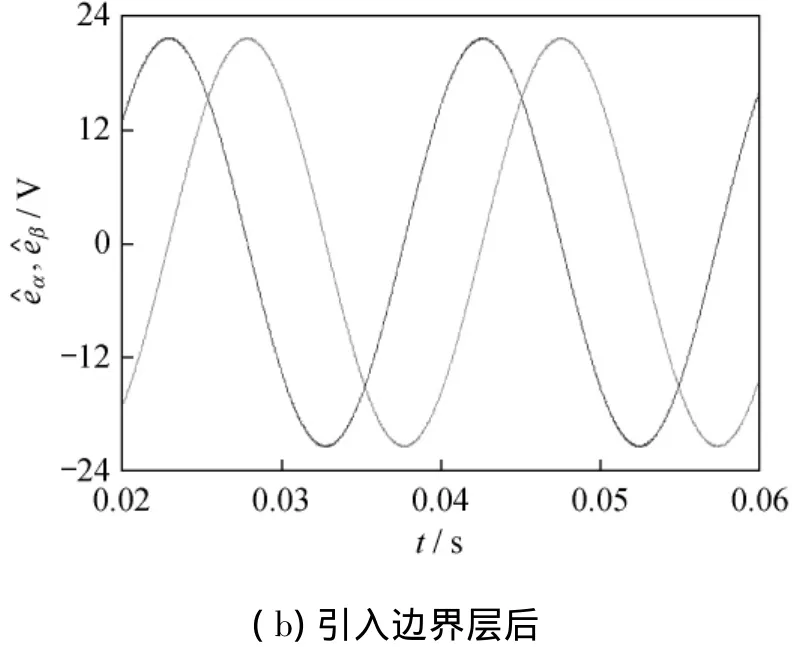
图4 滑模观测器所估算的反电势值
试验所用PMSM参数与仿真时一样。图6(a)~(d)分别为引入边界层前的电流、反电动势、转子位置角估算值及负载电流为5 A下马鞍形波和相电流波形;图7(a)~(d)分别为引入边界层后的电流、反电动势、转子位置角估算值及负载电流为5 A下马鞍形波和相电流波形。从中可以发现,未引入边界层时,估算的电流、反电势均存在高频抖振,估算的电机转子位置角与实际角度存在较大误差,负载情况下,相电流也存在抖动;引入边界层后,估算的电流、反电势都较为光滑,估算的转子位置角接近实际位置角,负载情况下,相电流也更趋于正弦。

图5 电机实际角度和估算角度


图6 引入边界层前

图7 引入边界层后
4 结 语
本文根据滑模变结构控制理论,构造了SMO,并采用边界层法来削弱抖振问题。仿真和试验结果表明了利用SMO能够估算PMSM的转子位置,采用边界层法可以有效削弱滑模控制的抖振问题,使估算得到的转子位置角变得更为平滑,电机运行更加平稳。
[1]Hoque M A,Rahman M A.Speed and position sensorless permanent magnet synchronous motor drives[C]∥Canadian Conference on Electrical and Computer Engineering,1994(2):689-692.
[2]Bolognani S,Tubiana L,Zigliotto M.EKF-based sensorless IPM synchronous motor drive for flux-weakening applications[J].IEEE Transactions on Industry Applications,2003(39):768-775.
[3]Piippo A,Luomi J.Adaptive observer combined with HF signal injection for sensorless control of PMSM drives[C]∥IEEE International Conference on Electric Machines and Drives,2005(2):674-681.
[4]Rasmussen H,Vadstrup R,Borsting H.Adaptive observer for speed sensorless PM motor control[C]∥Conf Rec of the 38th Industry Applications Conference,IAS,2003(1):599-603.
[5]Corley M J,Lorenz R D.Rotor position and velocity estimation for a permanent magnet synchronous machine at standstill and high speeds[C]∥IEEE IAS,1996(1):36-41.
[6]Schroedl M.Operation of the permanent magnet synchronous machine without a mechanical sensor[C]∥4th IEEE Conference on Power Electronics and Variable-speed Drives,1990(1):51-56.
[7]Schrodl M,Lambeck M.Statistic properties of the INFORM method for highly dynamic sensorless control of PM motors down to standstill[C]∥The 29th Annual Conference of the IEEE Industrial Electronics Society,IECON,2003(2):1479-1486.
[8]王丰尧.滑模变结构控制[M].北京:机械工业出版社,1998.
[9]王成元,夏加宽,孙宜标.现代电机控制技术[M].北京:机械工业出版社,2009.
[10]吴春华,陈国呈,孙承波.基于滑模观测器的无传感器永磁同步电机矢量控制系统[J].电工电能新技术,2006,25(2):1-4.
[11]Kenneth R.Buckholtz.Approach angle-based switching function for sliding mode control design[C]∥A-merican Control Conference,2002:2368-2373.
