基于复合前馈控制的交流位置伺服系统动态特性

邹金红， 朱玉川

(赣江职业技术学院，江西南昌 330108)

0 引言

将永磁同步电动机(Permanent Magnet Synchronous Motor，PMSM)位置伺服系统采用电流控制、速度控制和位置控制分开进行，实现三环串级控制可以获得更加可靠的伺服性能和动态跟踪性能。其传统串级控制策略中，电流环采用滞环控制方式，保证电流环的快速响应。速度环采用PI控制规律，以保证进行稳定的速度控制，使其定位时不产生振荡。位置环通常采用比例控制规律来保证位置控制的高精度和良好的跟踪性能。由这种经典控制组成的串级控制结构虽然具有结构简单、可靠性强、稳态精度高、实现容易等诸多优点，但系统的快速性、动态跟踪精度、抗干扰能力，以及对系统参数摄动的鲁棒性都不够理想。在位置伺服系统要求速度跟踪和加速度跟踪时，这种经典控制不能满足其位置控制的快速、高精度的要求［1］。本文研究了将复合前馈控制策略应用到交流位置伺服系统的位置环控制器设计，从而组成PMSM位置伺服系统串级复合控制器。该结构不仅可解决单一滑模控制器控制位置和速度变量带来的系统限幅问题，还进一步增强了系统抗干扰能力，提高了其动态跟踪精度，具有良好的控制性能。

1 PMSM位置伺服系统组成

本文将永磁同步伺服电动机应用于位置伺服系统，构成数字交流伺服系统，即以交流永磁同步伺服电动机为执行元件，系统速度环和位置环控制采用数字控制，其电气结构原理如图1所示。

图1 PMSM位置伺服系统结构原理图

2 基于磁场定向控制的PMSM线性化解耦数学模型

永磁同步伺服电动机的模型是一个多变量非线性的状态模型，为使伺服系统控制灵活、方便，响应快，控制精度高，必须实现交、直轴电流的解耦控制，电流解耦控制虽然得到的是近似线性解耦模型，但却容易实现，只要采用比较好的处理方式，该方法不仅能够获得快速高精度的力矩控制，而且控制电路简单，实现较方便，且使三相永磁同步伺服电机在动、静态均能得到近似解耦控制［2-3］。采用按转子磁极位置定向的矢量控制可以认为定子电流励磁分量Id≡0。为分析简化，作如下建模假设:(1)忽略饱和效应;(2)电动机气隙磁场均匀分布，感应反电动势呈正弦波状;(3)磁滞及涡流损耗不计;(4)转子上无励磁绕组。

根据以上假设，如图2所示，可写出转子坐标系即dq坐标系下系统的线性化数学模型。

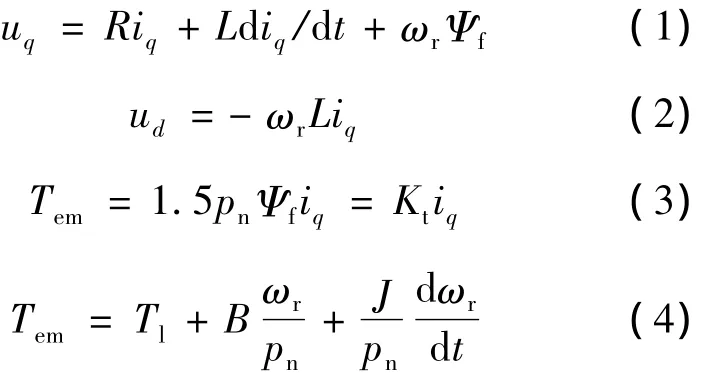
式中:ud，uq——dq坐标系上的电枢电压分量;

id，iq——dq坐标系上的电枢电流分量;

L——dq坐标系上的等效电枢电感(L=Ld=Lq);

R，ωr——电枢绕组电阻和dq坐标系的电角速度;

Ψf，pn——永久磁铁对应的转子磁链和电机极对数。

图2 PMSM转子坐标系

3 控制器设计

3.1 速度环控制器设计

交流位置伺服系统速度控制器采用数字式PI控制，根据PMSM数学模型将三个独立的电流环用一个等效的转矩电流环代替，速度反馈系数为Kw。在PMSM位置伺服系统中电流环节可以等效成为一阶惯性环节，选择速度环控制器为PI调节器，其传递函数为G(s)=Ks(1+1/Tss)，Ks、Ts分别为速度环调节器的放大倍数和积分时间常数，则速度环PI控制动态结构如图3所示［4-5］。

图3 速度环PI控制动态结构框图

根据图3，可得出速度环的开环传递函数:

由式(5)可知，转速环可以按典型的Ⅱ型系统来设计。定义变量h为频宽，根据典型Ⅱ型系统设计参数公式:

3.2 位置环复合前馈控制器设计

3.2.1 比例控制

作为连续的跟踪控制，交流位置伺服系统不希望位置出现超调和振荡，以免造成位置控制精度下降。因此，位置一般采用比例调节器，将位置伺服系统校正为典型的Ⅰ型系统。为保证控制精度，减小稳态运行时的位置偏差，应尽可能提高位置控制增益，并选择尽可能低的跟踪速度，经典位置环控制就是采用比例控制。

由于位置伺服系统要求快速响应并且无超调，所以应使位置伺服系统处于临界阻尼或过阻尼状态。当校正后速度控制环节的截止频率1/T1确定后，位置环增益KP可由ζ≥1这个条件确定:

其中:KP=1/4T1时为最优位置控制环增益。

3.2.2 复合前馈控制器设计

由于交流位置伺服系统位置环截止频率远小于速度环各时间常数的倒数，速度环的闭环传递函数可近似等效为一阶惯性环节，这样的处理在理论和实践中均能真实反映速度环的特性，并且能使位置环的设计大大简化，也易于分析伺服系统的稳定性等。交流位置伺服系统位置环复合前馈控制等效结构图如图4所示。

图4 位置环复合前馈控制等效结构图

根据式(9)考虑对交流位置伺服系统速度跟踪信号和正弦跟踪信号进行前馈补偿，则前馈补偿传递函数参数设计为

4 仿真研究

传统的经典PID控制在系统阶跃响应方面具有较好的性能，但系统在作等速跟踪及正弦跟踪时稳态误差较大。前馈控制是解决动态输入信号时控制精度较好的措施，前馈控制通过引入输入信号的一阶或二阶微分作为控制输出的一部分，与反馈控制相结合可以得到较高的静态精度和稳态跟踪精度。这里速度环采用PI控制策略，位置环反馈控制采用纯比例控制，前馈控制采用输入信号的一阶微分与二阶微分的组合控制，从而组成基于PI速度环控制的交流位置伺服系统串级复合前馈控制。其仿真模型如图5所示。

在MATLAB/Simulink中建立交流位置伺服系统仿真模型如图6所示，进行控制器参数设计与计算机仿真。系统主要参数如下:系统电机及负载转动惯量经折算后为 J=8.627×10－3kg·m2;系统不平衡力矩和摩擦力矩经折算后为4.86 N·m;系统外干扰力矩为10 N·m;电磁转矩系数Kt=1.11 N·m/A;阻尼系数B=1.43×10－4N·m·s;定子电阻 Ra=2.6 Ω;绕组电感Ld=Lq=50 ×10－3H;额定电流Ie=6.4 A;允许最大电流Imax=12.8 A;磁极对数Pn=4。

考虑伺服系统机械减速比，当系统参考输入为100 rad时响应曲线如图7～12所示。其中:图7和图8在0.2 s负载突加10 N·m的干扰力矩，等速输入为单位斜坡信号，正弦跟踪等效正弦输入信号为196 sin 0.713 6t。

图5 交流位置伺服系统串级复合前馈控制结构图

图6 交流位置伺服系统复合前馈控制仿真模型

图8 复合控制等速误差

图9 PID控制正弦误差(J=J0)

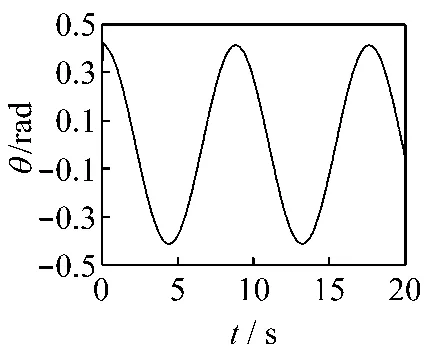
图10 复合控制正弦误差(J=J0)

如图8～13所示，复合前馈控制策略对等速跟踪具有较明显的作用，表现在其稳态跟踪误差接近于零，对于正弦跟踪，复合前馈控制策略仍然具有减小其稳态误差的作用，但对惯量变化敏感，加大惯量，跟踪初期表现为抖动峰值加大，进入稳态跟踪时间加长。

图11 PID控制正弦误差(J=2J0)

图12 复合控制正弦误差(J=2J0)

5 结 语

本文针对永磁交流位置伺服系统等速跟踪与正弦跟踪稳态精度低的缺点，提出了数字PMSM位置伺服系统复合控制结构方案，同时将PI控制与复合前馈控制应用于系统速度环和位置环设计，从而组成串级复合控制。计算机仿真结果表明，该控制策略对于等速输入与正弦输入信号可显著降低其稳态输出误差，大大提高其跟踪精度。

［1］秦忆.现代交流伺服系统［M］.武汉:华中理工大学出版社，1995.

［2］史晓娟.虚拟轴机床滑模变结构位置控制的研究［D］.西安:西安交通大学，2002.

［3］Kuo-Kai Shyu，Chiu-Keng Lai，Yao-Wen Tsai，et al.A newly robust controller design for the position control of permanent-magnet synchronous motor［J］.IEEE Transactions on Industrial Electronic(S0278-0046)，2002，49(3):558-565.

［4］段广仁.线性系统理论［M］.哈尔滨:哈尔滨工业大学出版社，1998.

［5］舒志兵.交流伺服运动控制系统［M］.北京:清华大学出版社，2006.