向量似变分不等式的间隙函数的可微性和灵敏性
2011-06-02刘学文谭仁新
张 悦,刘学文,谭仁新
(重庆师范大学数学学院,重庆 400047)
设S是Rm中的闭凸点锥,且intS≠∅,K是Rn中任意给定的非空紧子集,L Rn,R( )m是表示从Rn到Rm的所有线性连续算子的集合,映射F:Rn→L( Rn,Rm),单值映射η:K×K→Rn。向量似变分不等式问题(VVLI)就是求 x∈K,使得对任意的 y∈K,有〈F(x),η(x,y)〉∉ -S{0Rm}。弱向量似变分不等式问题(WVVLI)就是:求 x∈K,使得对任意的 y∈K,有〈F(x),η(x,y)〉∉ -intS。
本文令η(x,y)=t(x)-t(y),其中t:K→Rn单值映射,则(VVLI)问题变为:求x∈K,使得对任意的y∈K,有〈F(x),t(x)-t(y)〉∉ -S{0Rm},即(VVLI)*;求x∈K,使得对任意的y∈K,有〈F(x),t(x)-t(y)〉∉ -intS,即(WVVLI)*问题。
当t是恒等映射,即对任意的x∈K,有t(x)=x,则(VVLI)*和(WVVLI)*就退化为一般的向量变分不等式和弱向量变分步等式,因此它们分别是向量变分不等式和弱向量变分不等式中更广的形式。
1 基本知识
假设L Rn,R( )m是从Rn到Rm的所有线性连续算子的集合。对任意A∈L Rn,R( )m,A的模为
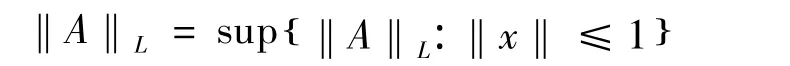
Rn是有限维空间,那么L Rn,R( )m也是有限维Banach空间。
定义1[1]称向量值函数 F:K→L Rn,R( )m在 x0处 Frechet可微,如果存在一个线性连续算子Ψ:Rn→L Rn,R( )m,使得:
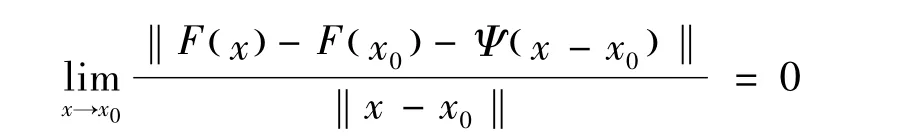
则称Ψ为F在x0处的导数,记为▽F( x0)。如果对任意的x∈K,F在x处都可微,则称F在K上Frechet可微。
定义2[2-3]设 C 是 Rn中的非空子集,令,则:
定义3[4]设C是Rn中的非空子集,向量值函数Φ:Rn→Rm。
注1 如果Φ:Rn→Rn是恒等映射,即Φ(x)=x,∀x∈Rn,则C在处的Φ-相依锥就是C在处的相依锥,可见Φ-相依锥可看成是相依锥的推广。同理,Φ-邻接锥可以看成是邻接锥的推广。
命题1[4]设C是Rn的非空子集,向量值函数Φ:Rn→Rm在∈C处连续可微,如果,则
命题2[4]设C是Rn的非空紧子集,向量值函数Φ:Rn→Rm连续。令

定义4[2]称graphG为集值映射G:Rn→2Rm的图,如果
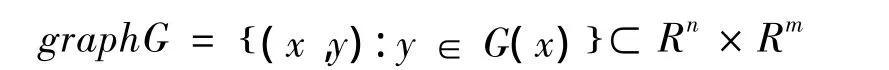
定义5[2]设,集值映射定义如下:
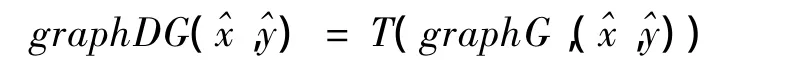
注2 由定义5可知:对任意的,当且仅当存在序列 { hn}⊂R+{0}:hn→0,{ ( xn,yn)}⊂Rn×Rm:(xn,yn)→(x,y)使得对任意的
引理1[5]设序列{αn}⊂R+:αn→0,{βn}⊂R+{0}:βn→0,则分别存在{αn}、{ βn}的子列 { αni}、使得
定义6[5]设S⊂Rm是闭凸点锥,A⊂Rm,记MaxSA和MaxintSA分别为A的极大点和弱极大点的集合,其中
1)对任意的a∈MaxSA,当且仅当a∈A,且不存在a*∈A,使得a*-a∈S{0Rm} 。
2)对任意的a∈MaxintSA,当且仅当a∈A,且不存在a*∈A,使得 a*-a∈intS。
定义7[6]称S的子集B是S的基,如果0Rm∉B,且对任意的d∈S,d≠0Rm可唯一表示成d=∂b,其中∂>0,b∈B。
引理2[7]设A是Rm中的非空紧子集,S是Rm中的闭凸点锥,且intS≠∅,则

2 集值映射G(x)的可微性
设K是Rn中的紧子集,F:Rn→L Rn,R( )m连续Frechet可微,t:K→Rn连续可微,设集值映射
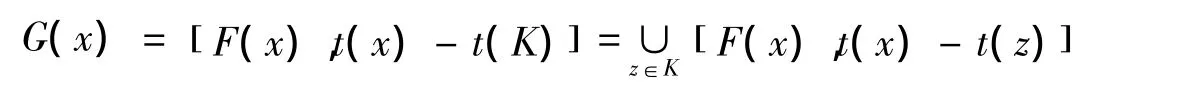
下面将讨论G(x)的可微性。
定理1设,且,则对任意的,有定义

证明假设,由定义5 知对任意的,存在序列 { hn}⊂R+{0}:hn→0,,{ ( xn,yn)}⊂Rn×Rm:(xn,yn)→(x,y),使得对任意的 n,有
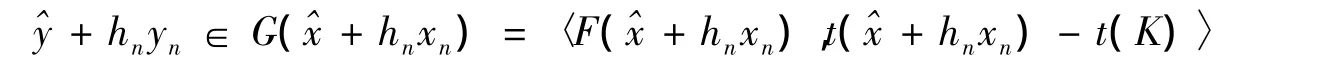

又由F连续Frechet可微,则可得F的Taylor展式为
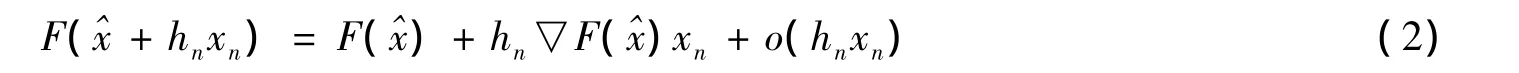
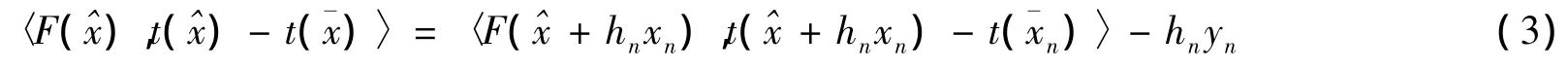
又由式(3)可得

由式(4)可得
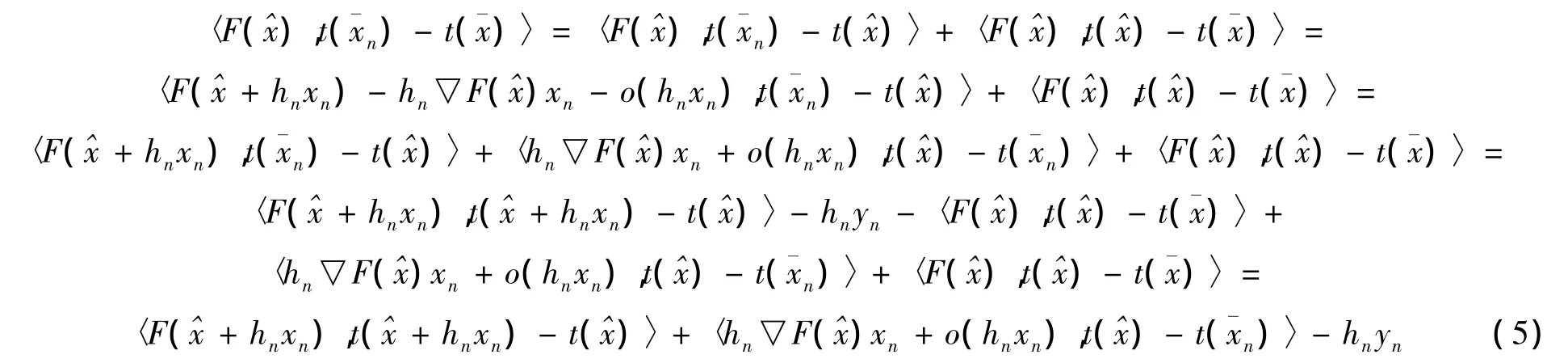
由式(5)得
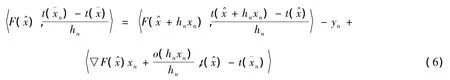

情况1假设存在子列使得,根据假设条件知:,与式(7)矛盾。
情况2 假设存在M>0,使得对任意的n有

因为hn→0,而t连续,故由式(8)可知只有

由于Rn是有限维空间,故可设,有定义知z∈Tt(K,¯x),又根据式(6)和(9)可得

即
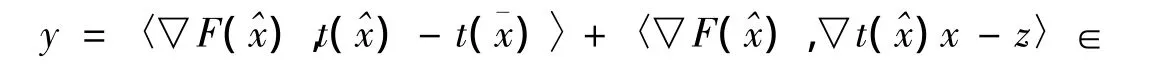
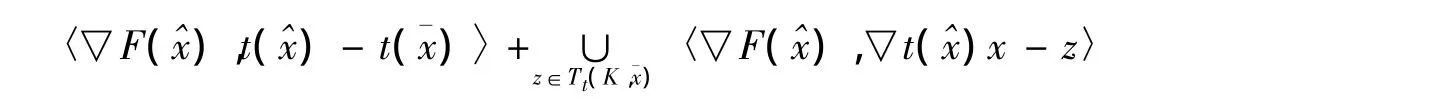
取序列 { xn}⊂Rn,{ yn}⊂Rm,使得 xn→x,令

则yn→y且
3 (VVLI)*与(WVVLI)*间隙函数的可微性与灵敏性
定义8 设S是Rm中的闭凸点锥,且intS≠∅,集值映射N:Rn→2Rm是向量似变分不等式(VVLI)*的间隙函数,如果
定义9 设S是Rm中的闭凸点锥,且intS≠∅。集值映射W:Rn→2Rm是向量似变分不等式(WVVLI)*的间隙函数,如果
命题3 设S是Rm中的闭凸点锥,且intS≠∅,
1)集值映射N:Rn→2Rm,N(x):=MaxS[F(x),t(x)-t(K)],x∈K,则N(x)是(VVLI)*的间隙函数;
2)设集值映射 W:Rn→2Rm,W(x):=MaxintS[F(x),t(x)-t(K)],x∈K,则 W(x)是(WVVLI)*的间隙函数。
证明
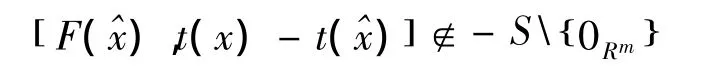

对于2)的证明与1)类似,只需将S和MaxS分别换成是intS和MaxintS即可。
定理2设,且,则对任意的,有
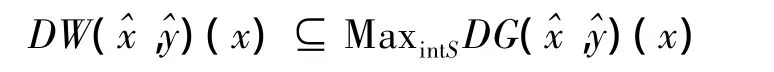
证明假设,显然有如果,则根据极大元的定义,存在,使得

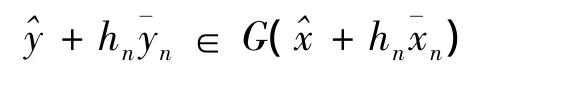
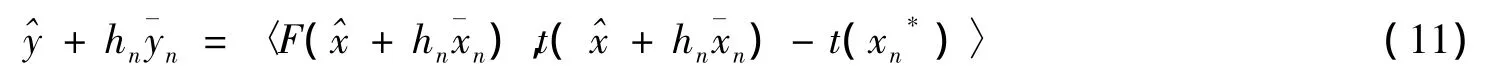
F连续Frechet可微,则可得F的Taylor展式

由式(12)、(13),有
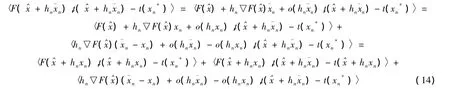
令

由式(11)、(14)有


定理3设,且
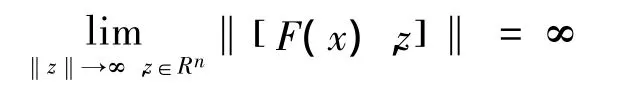

证明因为N(x)⊆W(x),故由定理2可知结论成立。
引理3 设,且,则对任意的,有
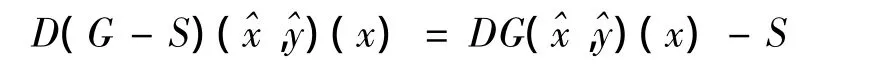
其中(G-S)(x)=G(x)-S。
证明显然

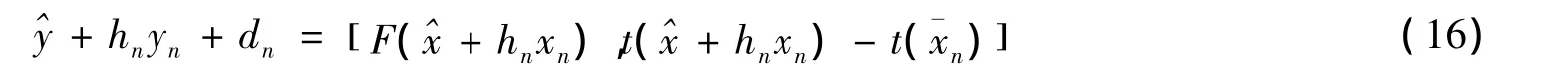

如果d≠0Rm,则与矛盾。故d=0Rm,即dn→0Rm。对 d{ }n分2种情况讨论。
情况1 存在 n0,使得当 n≥n0时,dn=0Rm,则
情况2 存在 { d }的子列 { d },不妨仍记为 { d },满足 d≠0,∀n,则有界,否则
nninnRm无界。不妨设,于是S有一个紧基,再由文献[8]中的引理3.1有

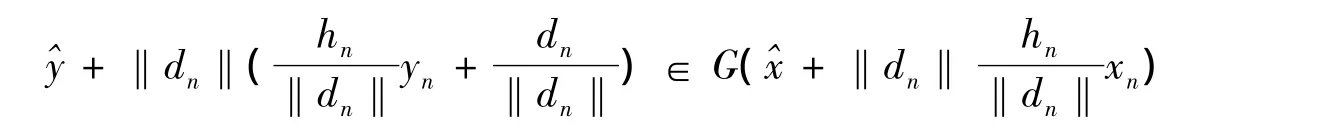

反之,由命题1[15]可知
定理4 设,如果,则对任意的,有
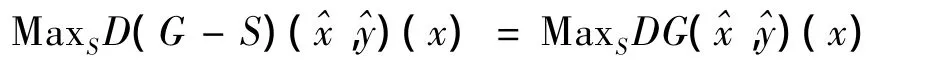
证明由引理3得,所以

4 (VVLI)*与(WVVLI)*的最优性条件
定理5 假设下面条件成立:
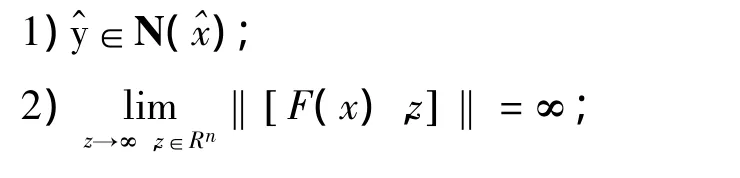
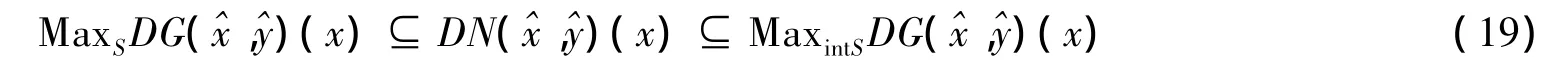
证明因为N(x)⊆G(x),所以,又由条件3)可得{0Rm}。K是紧集,所以t(K)是紧集,对任意固定的x∈K,所以G(x)也是紧集。因此由引理2有G(x)-S=N(x)-S。
由定理4有
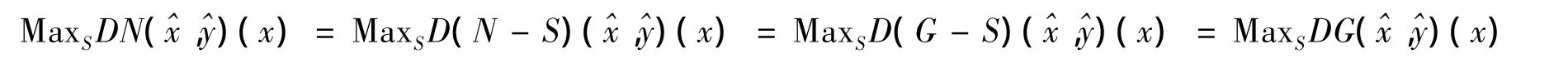
引理4[6]设S有一个基是一个非空闭凸锥,且,则也有一个基。
定理6假设下面的条件:

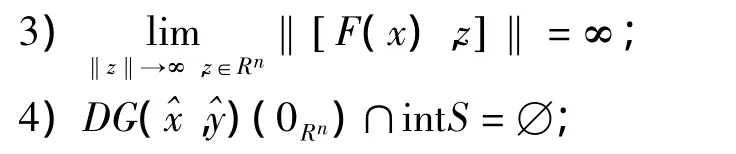
成立,则∀x∈Dom(DN(^x,^y));,
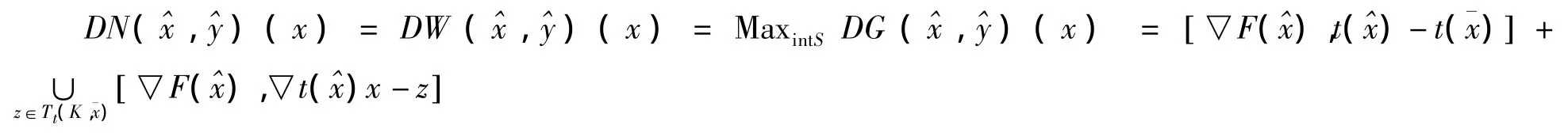
证明由N(x)⊆W(x)和定理4,只需证明

K是紧集,对任意固定的x∈K,有t(K)是紧集,所以G(x)也是紧集。由引理2有,再由定理 3 有
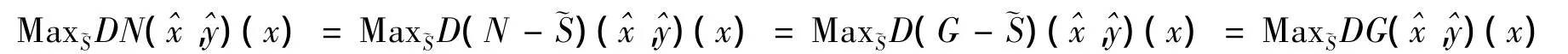
推论1 假设下面的条件:



证明由定理2和定理5直接可得结论成立。
定理7设,如果是(WVVLI)*的解,则

证明设是(WVVLI)*的解,则对任意的
定理8 假设下面的条件:
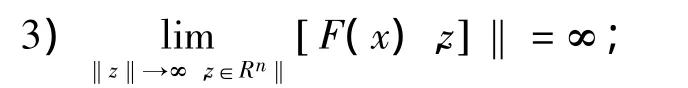
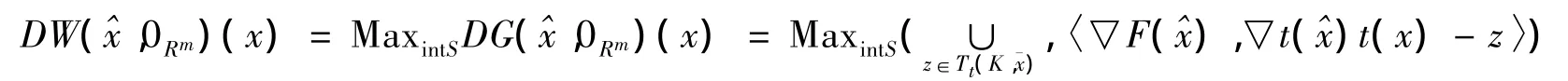
证明是(WVVLI)*的解,0Rm∈MaxSG(x),由定理7知
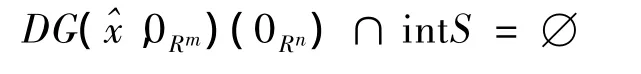
再由推论1知结论成立。
定理9 假设下面的条件:
2)存在闭凸锥 ˜S,满足 ˜S�R{ }m⊂intS;
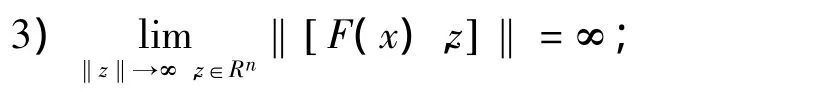

证明由于是(VVLI)*的解,0Rm∈MaxSG(x),根据定理7可得

再由定理6可知结论成立。
[1]游兆勇,龚怀玉,徐宗本.非线性分析[M]西安:西安交通大学出版社,1991.
[2]Abuin J P,Frankowska H.Set-Valued Analysis[M].Boston:Birhauser,1990.
[3]Kalashnikov V,Jadamba B,Khan A A.First and second-order optimization conditions in set optimization.In:Dempe,S.Kalashnikov,V.(eds.)Optimization with Multivalued appings[M].Berlin:Springer,2006:265 -276.
[4]Meng K W,Li S J.Differential and sensitivity properties of gap functions for Minty vector variational inequalities[J].Math A-nal Appl,2008,337:86 -398.
[5]Li S J,Yan H,Chen G Y.Differential and sensitivity properties of gap functions for vector variational inequalities[J].Math Methods Oper Res,2003,57:377 -391.
[6]Tanino T.Sensitivity analysis in multiobjective optimization[J].Optim Theory Appl,1988,56:479 -499.
[7]Li S J,Chen G Y,Lee G M.Minimax theorems for set-valued mappings[J].Optim Theory Appl,2000,106:183 -200.
[8]Shi D S.Contingent derivative of the perturvation map in multiobjective optimization[J].Optim Theorey Appl,1991,70:385 -396.
