公路边坡变形监测数据的小波阈值消噪方法*
2011-06-02姜越川
姜越川
(长沙理工大学华罡科技有限责任公司,湖南长沙 410076)
公路边坡变形监测数据的小波阈值消噪方法*
姜越川
(长沙理工大学华罡科技有限责任公司,湖南长沙 410076)
基于小波分析理论,介绍小波阈值消噪中阈值函数的选取和阈值的具体估计方法,并对阈值函数的选取进行比较分析。以工程实例为背景,就公路边坡变形监测数据消噪前后的信噪比和均方根误差2个指标对各种阈值方法进行对比分析。理论分析和应用实例的结果表明,几乎硬阈值方法比Garrote阈值方法能更好地恢复被噪声湮没的公路边坡局部变形信息。
边坡工程;变形监测;小波阈值函数;信噪比
公路边坡监测数据是公路边坡稳定性分析的重要科学依据,其可靠性和准确性直接影响到公路边坡稳定评判的结果。实际上,公路边坡由于受外界多种客观条件的影响,如施工条件、气候条件、测量仪器、测量人员等,导致边坡监测数据中往往包含有误差即噪声,很难准确判定该非平稳信号是边坡体本身变形突变的表现,还是噪声对其影响造成的突变现象,或是二者的综合体现。因为这些突变的影响在信号曲线中都表现为尖峰和突变,且都处于信号的高频部分。要准确分析这类信号,须采用相关的信号分析理论先对信号进行正确的分析处理,去除噪声产生的高频量,保留边坡本身突变产生的高频量[1]。
采用GPS技术监测公路边坡的变形已经是一个很成熟的技术。然而,GPS信号从发射到接收的过程中受到多种误差的影响,包括GPS卫星自身的钟差、卫星轨道误差,信号在传播介质中受到的电离层延迟和对流层延迟,以及地面环境效应,如多路径效应影响、杂波信号干扰等。因此,为了获得令人满意的监测结果,如何消除或削弱误差(即噪声)一直是变形监测数据处理研究的热点[2-9]。其中采用小波阈值收缩法消噪是目前研究最为广泛的去噪方法。近年来,随着小波理论研究的不断深入,其应用也得到了迅猛发展。小波去噪法一般有3类:第1类是基于小波变换模极大值原理;第2类是基于阀值的小波降噪法;第3类是基于小波系数区域相关性的去噪法。而小波阈值消噪方法有2个关键点:阈值函数的选取和阈值的估计方法,从某种程度上说,它直接关系到信号消噪的质量。在比较硬阈值方法、软阈值方法、几乎硬阈值方法和Garrote阈值方法对边坡变形的信噪比及均方根误差数据分析上看,几乎硬阈值方法和Garrote阈值方法都兼顾了软、硬阈值方法的优点,从滤波的效果上看,几乎硬阈值方法比Garrote阈值方法在效果上更好。本文对小波阈值消噪中的关键点进行了分析比较,结合某公路边坡变形监测数据进行了分析,得到了一些有用的结论。
1 小波阈值滤波原理
小波滤波基于小波变换的“集中”或“聚焦”能力。一般认为,信号经小波变换后,由信号产生的小波系数包含有信号的重要信息,其幅值较大,但数目较少,而噪声对应的小波系数幅值小、数目多。通过在不同尺度上选取合适的阈值,并将小于该阈值的小波系数置零或弱化,而保留大于阈值的小波系数,从而使信号中的噪声得到有效抑制,最后经小波逆变换,得到滤波后的重构信号[10]。小波阈值收缩法去噪的关键是要解决2个主要问题:阈值函数的选取和阈值的具体估计。
1.1 阈值函数的选取分析及比较
软、硬阈值方法虽然得到了广泛应用,也取得了较好的效果,但2种方法本身都有一些潜在的缺点。为了克服软、硬阈值法的缺点,Gao等提出的半软阈值法可以兼顾软、硬的优点,但要估计2个阈值,实现起来比较困难。在软阈值方法的基础上,Breiman提出的Garrote阈值方法可以兼顾软、硬的优点,Donoho提出的几乎硬阈值方法也有效地克服了软、硬阈值方法的缺点[10]。
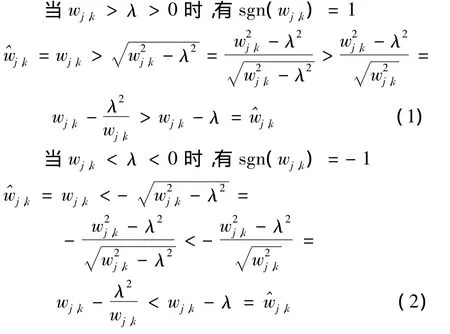
几乎硬阈值方法和Garrote阈值方法都较好地克服了硬阈值方法的不连续性缺点,由式(1)和(2)可知,几乎硬阈值方法比Garrote阈值方法更加逼近硬阈值方法,则几乎硬阈值方法比Garrote阈值方法能更有效地克服软阈值方法恒定偏差的缺点。
1.2 阈值的具体估计
由于阈值λ的选取比较灵活,有多种选取规则,对于阈值的选取主要有自适应阈值、启发式阈值、通用阈值和极大极小阈值等4种阈值选择规则[10]。对噪声进行小波分解时,产生的高频系数向量是有用信号和噪声信号的高频系数的叠加。由于自适应和极大极小阈值选取规则比较保守,仅将部分系数置零,因此在信号的高频信息有很少一部分在噪声范围内时,这2种阈值十分有用,可以将弱小信号提取出来;而启发式阈值和通用阈值选取规则,在去除噪声时更为有效,但是可能将有用信号的高频部分当作噪声信号除去。可以根据不同的噪声特点,选择相应的阈值处理方法。
固定(通用)阈值是针对多维独立正态变量联合分布,在维数趋向无穷时得出的结论,是基于最小最大估计得出的最大阈值,阈值λ的选取满足
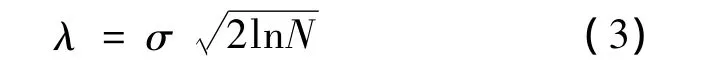
2 公路边坡变形监测数据分析
对某公路边坡变形采用GPS技术监测,布设点G06与G11为监测基准点,在公路边坡中部及其两侧布设3个监测变形点0P03,0P04与0P05。边坡侧部监测点0P04 Y方向(水平位移)的GPS变形监测数据如图1所示,其中GPS监测数据在期数7,11,12 d处受到的外界干扰较大,产生了明显的局部变形特征信息。

图1 点0P04 Y方向变形数据Fig.1 Deformation data of point 0P04 in Y direction
为说明几乎硬阈值方法去噪的优越性,采用db3小波基函数,对该信号进行3层分解去噪处理,并用硬、软阈值方法、Garrote阈值方法进行对比实验。

图2 消噪的变形数据Fig.2 The deformation data of de-noising
由图2可以看出,由于硬阈值函数的不连续性,导致去噪后曲线在GPS期数11 d处有明显振荡、折线现象;软阈值方法去噪后曲线虽光滑,但由于估计小波系数和带噪小波系数间有恒定的偏差,信号重构后处过于光滑,基本上不能保留边坡变形的局部变形特征信息;Garrote阈值方法兼顾了软、硬阈值方法的优点,去噪后曲线相对光滑,没有明显振荡、折线现象,在GPS期数7 d处、12 d处都略微保留了局部变形特征信息,但在期数11 d处仍然没有反映出边坡变形的局部变形特征信息。几乎硬阈值方法克服了软、硬阈值方法的缺点,去噪后曲线相对光滑,没有较大振荡、折线现象,在期数7 d处、11 d处、12 d处较好地保留了边坡变形的局部变形特征信息。从而得到更接近真实值的数据,也更好地反映公路边坡的水平位移变形规律,给后期的变形预报分析提供了更精确的数据。
为了从数值上反映几乎硬阈值方法的优越性,下面给出4种阈值去噪方法的信噪比、均方根误差。从滤波的效果上看,信号的信噪比越高,均方根误差越小,则消噪信号越接近于原始信号,去噪效果越好。
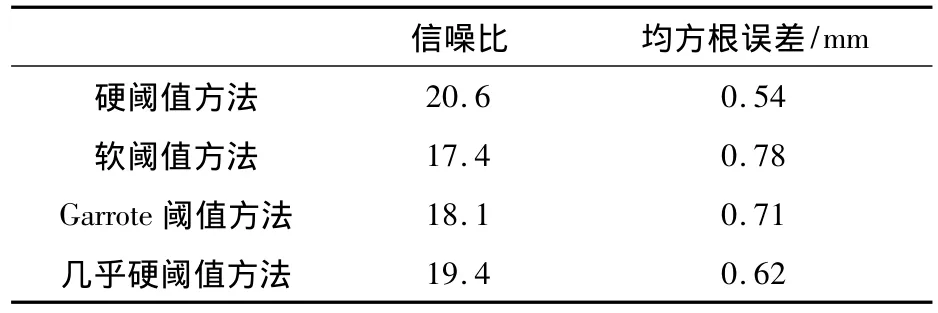
表1 4种方法对去噪效果的比较Table 1 De-noising result contrast between 4 methods
从表1中看出,硬阈值方法得到的信噪比最大,软阈值方法得到的信噪比最小,几乎硬阈值方法和Garrote阈值方法介于两者之间,几乎硬阈值方法得到信噪比又比Garrote阈值方法得到信噪比大;硬阈值方法得到的均方根误差最小,软阈值方法得到的均方根误差最大。几乎硬阈值方法和Garrote阈值方法介于两者之间,几乎硬阈值方法得到均方根误差又比Garrote阈值方法得到均方根误差小。因此,几乎硬阈值方法和Garrote阈值方法都兼顾了软、硬阈值方法的优点,从滤波的效果上看,几乎硬阈值方法比Garrote阈值方法去噪效果好。
3 结论
几乎硬阈值方法和Garrote阈值方法都能对变形中的噪声进行分离消除,从而较大程度地减小误差的影响,获得公路边坡变形的真实信号。但从滤波的效果上看,几乎硬阈值方法比Garrote阈值方法能更有效地恢复被噪声湮没的边坡局部变形信息,进一步提高消噪的精度与可靠性。工程实例表明,几乎硬阈值方法能更好地表现公路边坡水平位移的变形特征。
[1]梁桂兰,徐卫亚,谈小龙,等.岩石高边坡安全监测数据的小波变换去噪处理[J].岩石力学与工程学报,2008,27(9):1837 -1844.
LIANG Gui-lan,XU Wei-ya,TAN Xiao-long,et al.Denoising processing of safety monitoring data for high rock slope based on wavelet transform[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(9):1837 -1844.
[2]田胜利,周拥军,葛修润,等.基于小波分解的建筑物变形监测数据处理[J].岩石力学与工程学报,2004,22(7):1856-1860.
TIAN Sheng-li,ZHOU Yong-jun,GE Xiu-run,et al.Processing of monitoring data of building deformation based on wavelet transform[J].Chinese Journal of Rock Mechanics and Engineering,2004,22(7):1856 -1860.
[3]阎 振,陆 阳,余建华,等.小波分析在边坡深部水平位移监测数据降噪中的应用[J].中南公路工程,2007,32(2):41 -44,55.
YAN Zhen,LU Yang,YU Jian-hua,et al.Application of wavelet analysis to noise removal for slope’s displacement monitoring data[J].Central South Highway Engineering,2007,32(2):41 -44,55.
[4]李元松,李新平,代翼飞,等.小波神经网络在高陡边坡位移预测中的应用[J].武汉工程大学学报,2010,23(1):19-24.
LI Yuan-song,LI Xin-ping,DAI Yi-fei,et al.The application of wavelet neural network on displacement predicting for high - steep slope[J].Journal of Wuhan Institute of Technology,2010,23(1):19 -24.
[5]秦真珍,杨 帆,徐 佳.基于小波神经网络的边坡预报模型研究[J].城市勘测,2009,14(4):28 -32.
QIN Zhen-zhen,YANG Fan,XU Jia.The study of slope forecasting model based on wavelet neural network[J].Urban Geotechnical Investigation & Surveying,2009,14(4):28-32.
[6]李长洪,范丽萍,郭俊温.小波神经网络在露天矿边坡变形预测中的应用[J].中国矿业,2010,22(7):56-59.
LI Chang-hong,FAN Li-ping,GUO Jun-wen.Application of wavelet neural network in open-pit mine slope deformation prediction [J].China Mining Magazine,2010,22(7):56-59.
[7]陈宗成,封良泉,董胜光.基于小波分析的光照电站边坡位移变形监测研究[J].北京测绘,2009,21(2):45-48.
CHEN Zong-cheng,FENG Liang-quan,DONG Shengguang.The research of irradiation station side slop displacement deformation monitoring based on wavelet analysis[J].Beijing Surveying and Mapping,2009,21(2):45-48.
[8]张 勤,蒋延臣,王秀萍.小波变换在变形监测中的应用研究[J].测绘工程,2005(3):8-10.
ZHANG Qin,JIANG Yan-chen,WANG Xiu-ping.Research on application of wavelet transform to deformation observation[J].Engineering of Surveying and Mapping,2005(3):8-10.
[9]吴继忠.GPS观测数据的小波阈值法消噪[J].大地测量与地球动力学,2008,9(4):79 -83.
WU Ji-zhong.De-noising of GPS observations with wavelet threshold method[J].Journal of Geodesy and Geodynamics,2009,9(4):79 -83.
[10]成礼智,王红霞,罗 永.小波理论与应用[M].北京:科学出版社,2004.
CHENG Li-zhi,WANG Hong-xia,LUO Yong.Wavelet theory and application [M].Beijing:Science Press,2004.
[11]黄声享,尹 晖,蒋 征.变形监测数据处理[M].武汉:武汉大学出版社,2004.
HUANG Sheng-xiang,YIN Hui,JIANG Zheng.Deformation monitoring data processing[M].Wuhan:Wuhan University Press,2004.
Wavelet thresholding de-noising method for road slope deformation monitoring data
JIANG Yue-chuan
(Changsha University of Science and Technology,Changsha 410076,China)
Based on the wavelet analysis principle,the estimation method and function choosing in de-noising of wavelet threshold was introduced in this paper,and comparative analysis of threshold function choosing was presented.Based on observed data from one road slope,the compare between the original and the modify signal after de-noising on evaluate index of SNR and MSE was proposed.According to the theoretical analysis and engineering projects,the almost- hard thresholding can be more effective than Garrote thresholding in taking the road slope local deformation characteristic information.
slope engineering;deformation monitoring;wavelet threshold function;SNR
U416.1+4
A
1672-7029(2011)03-0046-04
2011-05-09
姜越川(1968-),男,辽宁丹东人,工程师,从事道路工程研究
