不同编码激励的超声气体流量测量性能对比

蒲 诚，张 涛，綦 磊

(天津大学电气与自动化工程学院，天津 300072)

不同编码激励的超声气体流量测量性能对比

蒲 诚，张 涛，綦 磊

(天津大学电气与自动化工程学院，天津 300072)

对比研究了13位巴克码、2周期7位m序列(均为二进制相位调制)和线性调频3种典型脉冲压缩编码激励下，超声流量测量系统的性能．对接收信号进行脉冲压缩处理后，测得流速与横河1.0精度等级的涡街流量计读数比对，以评估其测量性能．结果表明，m序列激励下脉冲压缩输出旁瓣远高于理论值，而巴克码和线性调频激励时，旁瓣与理论值相差不超过10%．在3～19,m/s的实验流速范围内，相同时宽带宽积条件下，线性调频信号频谱与换能器带宽的匹配度最高，因此有最小的流速标准偏差和读数误差，巴克码次之，m序列最大．

超声气体流量测量；编码激励；脉冲压缩；性能对比

脉冲压缩编码[1]广泛应用于雷达，但在超声检测领域发展缓慢．其主要原因是，超声信号在介质中的频率衰减和非线性传播特性，导致接收到的编码信号失真，脉冲压缩性能劣化[2]．然而，随着传感器材料、制造工艺和信号处理方法的发展，脉冲压缩技术近20年已成功应用于医疗超声成像、超声测距，可有效提高信噪比和检测分辨率[3-4]．

传统的传播时间法超声流量测量系统，采用单脉冲或猝发脉冲(tone burst)作为激励信号．发射功率恒定条件下，脉冲越宽(带宽越小)，作用距离越大；脉冲越窄(带宽越大)，时间分辨率越高．同时提高时间/流速分辨率和作用距离是一对矛盾，为兼顾两者，可选择大时宽带宽积信号以及脉冲压缩技术，以提高信噪比和时延估计精度．这类信号[5]既有二进制编码，如巴克码(Barker)和m序列等，也包括线性调频(linear frequency modulation，LFM)，统称为脉冲压缩编码信号．早在1988年，文献[6]将此技术引入超声流量测量，并基于自相关函数旁瓣最小原则，选择了11位巴克码作为二进制调相激励信号．文献[7]使用线性调频激励和连续波相位差法，实现海上平台火炬尾气的超声流量监测，流速范围达0.3～80,m/s．Tanisawa等[8-9]近年来也致力于调频激励气体超声流量测量研究，认为调频信号有利于稳定声场分布，提高流速测量精度．但是，关于不同编码激励对超声流量测量影响的对比研究鲜见报道．Nowicki等[10]针对医学超声成像系统，用水听器测量了线性调频、巴克码和格雷码(Golay)3种不同编码激励的超声远场特性，并与单脉冲激励比较，发现脉冲压缩与窄脉冲激励产生的声场分布相似，更能有效抑制距离/时间旁瓣，其中格雷码激励系统的旁瓣水平最低．

然而，相对于超声测距、成像和无损检测所要求的主旁瓣比和分辨率[2]，脉冲压缩输出的峰值位置精度(即传播时间精度)是编码激励超声流量测量中更为重要的指标．理论上，只要旁瓣水平低于主峰，就可正确估计传播时间，从而精确测得流速．基于上述原理，笔者在标准表法气体流量实验装置上，以流速样本的读数误差和标准偏差为参考指标，对比研究了时宽带宽积相同的3种脉冲压缩编码，即巴克码、m序列和线性调频激励下的超声流量测量系统，前两者均为二进制相位调制(binary phase shift keying，2PSK)．

1 脉冲压缩编码激励的超声流量测量

脉冲压缩编码激励的超声流量测量原理如图1所示．用编码调制信号激励超声换能器，顺、逆流接收信号分别与预先存储的零流速基准信号作匹配滤波[5]，输出波形峰值对应的时间轴坐标即为超声信号顺、逆流传播时延tdn和tup，以此计算流速．

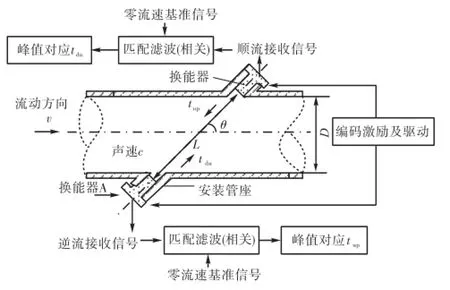
图1 脉冲压缩编码激励的超声流量测量原理Fig.1 Ultrasonic flow metering system with coded excitation and pulse compression

匹配滤波器是脉冲压缩处理的核心，数学上与相关处理等价，其时延估计性能用估计量标准偏差理论下界——克拉美·罗界(Cramer-Rao bound，CRB)[12]描述．超声流量测量系统中的信号一般为窄带信号，采用的带通形式[11]为

式中：σ为时延估计量的标准偏差；SNR为信噪比；T为测量时间；B为信号自功率谱带宽；f0为载波频率，对应超声换能器的中心工作频率．式(1)表明，相关时延估计的标准偏差，即流速标准偏差，与信噪比、时宽带宽积TB、中心频率以及相对带宽B/f0(fractional bandwidth)成反比；对窄带信号，B/f0≪1，相同信噪比和中心频率条件下，信号的时宽带宽积TB是决定测量精度的主要因素．传统激励信号，如单脉冲或猝发脉冲，其时宽带宽积接近于1[5]，而脉冲压缩信号的时宽带宽积可以远大于1．因此，当超声信号在流体介质中衰减较大，系统信噪比低时，如超声气体流量测量场合，使用TB≫1的编码调制激励，有更好的测量性能．

2 实验装置和方法

超声换能器为SensComp收发两用型压电换能器120kHF25，最大驱动电压峰峰值50,V，中心频率125,kHz，带宽10,kHz．使用标准表法常压空气流量实验装置，标准表为横河DY100型数字式旋涡流量计，流速小于35,m/s时，读数误差±1.0%．实验管段内径D＝150,mm，换能器以插入式Z型安装，轴线与水平夹角θ约为45.8°，如图1所示，声程长度L实测为242,mm，为保证实验管段内为充分发展的紊流，配置了足够长的上游直管段(20,D)．

由FPGA芯片ACEX1K30设计的编码激励超声流量测量平台[12]，其信号发生模块基于直接数字频率合成原理(direct digital frequency synthesizer，DDS)[13]，改变少数参数配置，就可产生各种编码和带宽的激励信号．接收信号经前置放大滤波后，使用NI公司的USB6251数据采集卡(16,bit，单通道最大采样速率1.25,MHz)进行A/D转换，其采样时钟和触发方式均选用外部源，由FPGA系统时序模块提供．顺、逆流接收信号，采样至上位机，分别与零流速下的基准信号作相关，测得顺、逆流传播时间，计算声程平均流速为

式中：v为声程平均流速；L为声程长度；θ为换能器轴线与水平管道轴线夹角，如图1所示．GB/T 18604—2001[14]中的单声道修正系数为

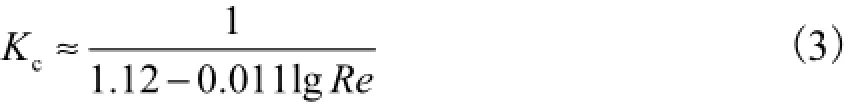
式中Re为雷诺数．将声程线速度转化为计算流量所需的面平均流速．此流速与温压补偿后的标准涡街测得流速比对，计算流速相对误差和标准偏差．

3 编码激励信号的选择

选择3种典型的脉冲压缩信号——巴克码、m序列和线性调频，对比研究了相同时宽带宽积(TB≈26)下，各种不同编码激励下的超声流量测量性能．理论上，TB越大，测量性能越好．但巴克序列最长13位[15]，要使其带宽与超声换能器10,kHz带宽匹配，相应码片宽度200,μs，则TBmax＝13×200,μs× 10,kHz＝26．m序列带宽也由码片宽度决定，最接近的序列长度是14位，即2周期7位m序列，因此TBm＝24．上述2种序列的载波频率均为125,kHz.线性调频信号的带宽为10,kHz，时宽2.6,ms，TBlfm＝26．三者TB值相近．

3.1 巴克码

巴克序列是一种二元伪随机序列，最长13位(1111100110101)．码片宽度200,μs，13位巴克码二进制相位调制的激励信号，其频谱如图2(a)所示．巴克序列具有良好的0和1相间的非周期自相关函数，旁瓣高度为1/N(N为序列长度)，如图2(b)所示．

3.2 m序列

m序列也称最大长度移位寄存器序列，由本原多项式生成[15]，长度为2n-1(n为大于1的自然数)．它的周期自相关函数很理想，峰值为1，其余值为-1/N(N为序列长度)，如图3(b)所示．但是m序列的非周期自相关特性并不理想，具有很高的旁瓣．码片宽度200,μs，2周期7位m序列(1110100)二进制相位调制的激励信号，其频谱如图3(a)所示．

3.3 线性调频

线性调频信号对多普勒频移不敏感，自相关函数具有sinc函数型包络(sinc x＝sin x/x)，-4,dB主瓣宽度为1/B(B为带宽)，第1旁瓣高度为-13.2,dB，如图4(b)所示．10,kHz带宽的线性调频信号，中心频率为125,kHz，持续时间为2.6,ms，频率变化率K＝B/T≈3.85×106,Hz/s，频谱如图4(a)所示．

图2 13位巴克序列相位调制信号的频谱和自相关函数Fig.2 Spectrum and auto-correlation function of signalphase modulated by 13 bit barker code

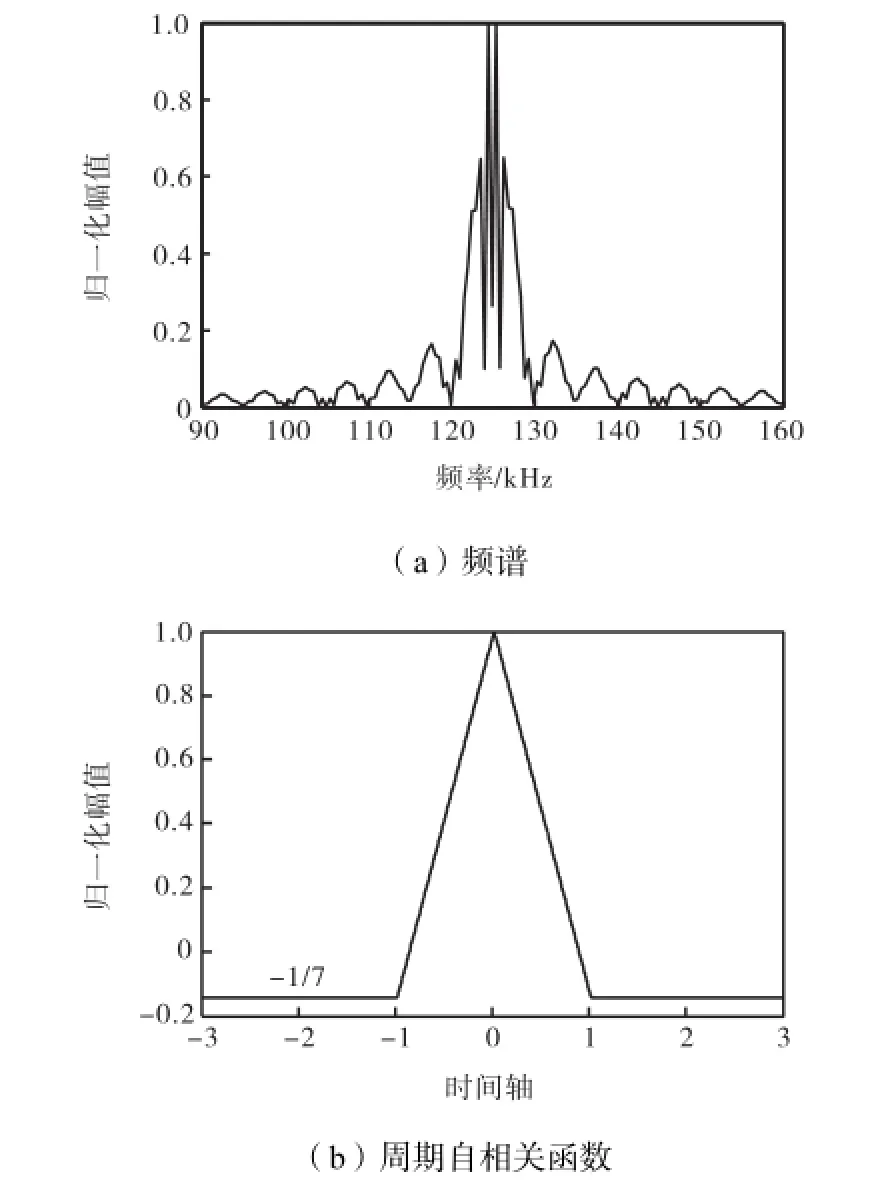
图3 2周期7位m序列相位调制信号的频谱和周期自相关函数Fig.3 Spectrum and periodic auto-correlation function of signal-phase modulated by 2 cycles of 7 bit m sequence

图4 线性调频信号频谱和自相关函数Fig.4 Spectrum and auto-correlation function of LFM signal

图5 13位巴克码2,PSK系统，200,m3/h，顺流波形Fig.5 Waveforms of 13 bit Barker code 2,PSK system at 200,m3/h，downstream

4 结果及讨论

图5(a)、6(a)、7(a)分别是标准流量200,m3/h时、13位巴克码、两周期7位m序列相位调制激励和线性调频激励下的顺流接收波形，图5(a)、6(a)的包络能看见明显的相位变化．图5(b)、6(b)、7(b)则是相应的脉冲压缩输出，均具有尖锐的主峰．但是，与巴克码和线性调频激励相比，m序列的旁瓣较高．依图顺序，三者的旁瓣主瓣比分别为0.084、0.287和0.239，而三者旁瓣主瓣比的理论值分别为0.077 (图2(b))、0.143(图3(b))和0.219(图4(b))由此可得，巴克码和线性调频激励下输出的旁瓣主瓣比与理论值相差10%左右，而m序列激励下的旁瓣主瓣比明显偏离理论值，这是由于其非周期自相关性能变差所致．值得注意的是，距离主峰1.4,ms左右处存在一幅值较大的峰，为二次回波，即由接收换能器界面法向反射至发射端，又由发射端反射至接收端的回波信号，对应的脉冲压缩输出．声程长度为242,mm，室温20,℃左右，理论声速约344,m/s，二次回波与主波间隔约242×2/344≈1.407,ms．

为进一步对比不同脉压编码激励系统的性能，以空气为介质，在工况(1个标准大气压，20,℃)流量200～1,200,m3/h(对应实验管段流速3～19,m/s)范围内，每隔100,m3/h进行检定，各流量点均采集100个样本．图8(a)是流速测量样本iv的标准偏差，且有

式中refv为温压补偿后的标准涡街测得流速参考值．

结果表明，相同时宽带宽积条件下，线性调频激励的流速偏差和读数误差最小，巴克码次之，m序列最大．这是因为超声换能器有限带宽10,kHz，相当于一带通滤波器，区间[120,kHz，130,kHz]之外的频率分量被滤除或衰减．对比图2(a)、3(a)和4(a)所示各编码激励的频谱，线性调频信号在以上区间的能量最集中，而巴克码和m序列频谱分布更分散，再加上m序列非周期自相关特性不理想，造成脉冲压缩输出失真程度变大，其峰值的偏移度和重复性也变差．

另外，无论何种编码，标准偏差和读数误差均随流速的增加而变大．这是由于流速变大时，流动噪声对超声信号参量，如幅值、相位等的调制作用较大，使得系统的信噪比减小，接收信号与标准信号的相关性减弱．读数误差均为负则是安装效应引起．如图1所示，实测声程长度L＞D/sin θ，因此流体在换能器与安装管座之间的凹槽形成旋涡，在小范围内改变了声信号的传播速度，使得传播时间差偏小．

图6 2周期7位m序列2,PSK系统，200,m3/h，顺流波形Fig.6 Waveforms of two cycles of 7-bit m sequence 2,PSKsystem at 200,m3/h，downstream

图7 线性调频激励系统，200,m3/h，顺流波形Fig.7 Waveforms of LFM system at 200,m3/h，downstream

图8 不同编码激励系统性能对比Fig.8 Comparison of systems with different coded excitations

5 结 语

超声流量测量中，使用脉冲压缩编码调制的激励信号，可提高信噪比和时延估计精度．笔者分析了巴克码、m序列和线性调频3种典型脉冲压缩信号的频谱及自相关函数特征，在基于FPGA的系统平台上，对比研究了上述3种激励下的流量测量性能．结果表明，2周期m序列的脉冲压缩输出有较高旁瓣，与理论值相差较大，而巴克码和线性调频的输出与理论形状一致．在相同的时宽带宽积条件下，线性调频信号与换能器的频谱匹配度最高，具有最小的流速标准偏差和读数误差；巴克码次之；有限周期的m序列最差．因此，在脉冲压缩编码激励的超声流量测量系统中，应根据超声换能器的频带特征和信号的自相关函数特征选择激励类型，以获得最优的流量测量性能．

［1］ Skolnik M I. 雷达系统导论[M]. 北京：电子工业出版社，2006. Skolnik M I. Introduction to Radar System[M]. Beijing：Electronics Industry Press，2006(in Chinese).

［2］ Chiao R Y，Hao Xiaohui. Coded excitation for diagnostic ultrasound：A system developer’s perspective[J].IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，2005，52(2)：160-170.

［3］ O’Donnell M. Coded excitation system for improving the penetration of real-time phased-array imaging systems [J]. IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，1992，39(3)：341-351.

［4］ Elmer H，Schweinzer H. High resolution ultrasonic distance measurement in air using coded signals [C]//IEEE Instrumentation and Measurement Technology Conference. Anchorage，AK，USA，2002：1565-1570.

［5］ 林茂庸，柯有安. 雷达信号理论[M]. 北京：国防工业出版社，1984.

Lin Maoyong，Ke Youan. Theory of Radar Signals[M]. Beijing：National Defense Industry Press，1984(in Chinese)．

［6］ Differential Correlation Analyzer： US：4787252[P]. 1988-11-29.

［7］ Mylvaganam F. Chirp excitation of ultrasonic probes and algorithm for filtering transit times in high-rangeability gas flow metering[J]. IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，1993，40(3)：193-215.

［8］ Saitou T，Tanisawa S，Hirose H. Basic examination of the FM ultrasonic flowmeter for gas[C]// SICE Annual Conference．Osaka，Japan，2002：1728-1731.

［9］ Tanisawa S，Hirose H. Study on a gas FM ultrasonic flow rate sensor for a small diameter pipe[C]// SICE Annual Conference．Sapporo，Japan，2004：521-524.

［10］ Nowicki A，Klimonda Z，Lewandowski M，et al. Comparison of sound fields generated by different coded excitations—experimental results[J]. Ultrasonics，2006，44(1)：121-129.

［11］ Quazi A H. An overview on the time delay estimate in active and passive systems for target localization[J]. IEEE Transactions on Acoustics，Speech，and Signal Processing，1981，29(3)：527-533.

［12］ 蒲 诚，张 涛，吕 方. 编码激励超声流量测量平台[J]. 传感器与微系统，2009，28(10)：85-87.

Pu Cheng，Zhang Tao，Lü Fang. An ultrasonic flow metering platform with coded excitation[J]. Transducer and Microsystem Technologies，2009，28(10)：85-87 (in Chinese)．

［13］ 董国伟，李秋明，赵 强，等. 基于FPGA的直接数字频率合成器的设计[J]. 仪器仪表学报，2006，

27(6)：877-879. Dong Guowei，Li Qiuming，Zhao Qiang，et al. Design of direct digital frequency synthesizer based on FPGA[J]. Chinese Journal of Scientific Instrument，2006，27(6)：877-879(in Chinese)．

［14］ 国家质量监督检验检疫总局．GB/T 18604-2001用气体超声流量计测量天然气流量[S]. 2001．

General Administration of Quality Supervision，Inspection and Quarantine of the People’s Republic of China. GB/T 18604-2001 Measurement of Natural Gas Flow by Ultrasonic Flow Meter[S]. 2001(in Chinese)．

［15］ Zepernick H J，Filger A. 伪随机信号处理——理论与应用[M]. 北京：电子工业出版社，2007．Zepernick H J，Filger A. Pseudo Random Signal Processing Theory and Application[M]. Beijing：Electronics Industry Press，2007(in Chinese)．

Performance Comparison of Ultrasonic Gas Flow Metering Systems with Different Coded Excitations

PU Cheng，ZHANG Tao，QI Lei
(School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China)

This paper reports the performance comparison of ultrasonic gas flow metering systems with three typical pulse compression coded excitations. In addition to the chirp signal，the excitation sequences phase-modulated with 13 bit Barker code and 2 cycles of 7 bit m sequence are investigated. Receiving signals are compressed to calculate the flow rate which can be compared with the reference provided by the Yokogawa vortex flowmeter(reading error± 1.0%). Results indicate that the main-peak side-lobe ratio(MSR)of the pulse compression output deviates seriously from the theoretical value when using m sequence excitation，while the ratio is not more than 10% when using Barker code and chirp signal. It is also found that at the similar time-bandwidth product and the experimental flow range of 3—19,m/s，the system energized by chirp signal has the smallest flow rate standard deviation as well as the reading error due to its most matching spectrum within the transducer bandwidth.

ultrasonic gas flow metering；coded excitation；pulse compression；performance comparison

TP216

A

0493-2137(2011)09-0768-06

2010-03-04；

2010-04-21.

国家高技术研究发展计划(863计划)资助项目(2008AA042207)．

蒲 诚（1981— ），男，博士研究生，pucheng2008@gmail.com．

张 涛，zt50@tju.edu.cn.