磁异常共轭元反演解释法研究

晏月平 ，戴前伟，蔡家雄 ，鲁光银

(1. 中南大学 地球科学与信息物理学院，湖南 长沙，410083；2. 湖南省有色地质勘查局，湖南 长沙，410000；3. 湖南省国土资源厅，湖南 长沙，410004)

以复变函数[1]为基础、建立于经典静位场理论基础之上的磁法勘探方法[2-3]，由于正演理论较其他地球物理勘探方法成熟，所以，率先在计算机上实现了一系列的反演方法和技术，尤其是近30年来，随着电子计算机的广泛应用，地球物理反演的理论和方法得到了极大的发展[4-5]。Backus-Gilbert反演理论[6]、广义逆矩阵理论、统计参数估计、最小二乘参数估计、最大似然法参数估计、正则化理论、约束最优化、动态规划、遗传算法[7]、神经网络法[8]等得到应用。这些方法在磁法反演上的共同特点是，在观测数据与模型之间建立一种函数关系，在解释过程中不断修改模型参数[9-10]，不断评价观测值与理论模型计算值的拟合程度，最后通过某种评判标准中断反演进程求得最终模型。它们的实质都是完全以位场理论为基础寻求获得稳定解和收敛速度的计算方法，由于过多依赖于计算技巧的运用，在理论上难以有实质性的突破，同时，这些方法在解释过程中有一系列近似条件的设定和线性方程组[11]的求解，这些过程势必导致误差累加，影响反演结果的真实性。特征点法[12]是一种简便而快速的定量解释方法，解释是以剖面磁异常特征为基础，但由于缺少完整的数学模型，依赖于经验积累和简单的几何运算，其定量计算结果难以取得好的效果，尤其对复杂异常或迭加异常，特征点解释法更是难以进行。本文作者提出的方法其理论原形可以追溯到特征点法，但方法的实质和求解过程远远超出了特征点法的概念范畴。它试图摆脱现有各类反演方法，以板状体磁异常为切入点，以磁异常平面和剖面特征为突破对象，通过提取异常共轭元等特征参数，建立磁异常图形变换的数理模型，并以变换图形的手段实现磁异常的反演解释，期望为磁法勘探的正反演计算提供新的途径。

1 板体磁场计算公式

对特定地理环境下的板状体，已知板体宽度2b，板体走向长度为2L，板体下延长度为l，上项埋深为h，板倾角为β，中心点坐标为x0等，如图1所示。若知道地磁场倾角I0、板体走向与磁北的夹角A和剖面内有效磁化倾角is，则剖面任意点处总强度磁异常ΔT计算公式[13]为：

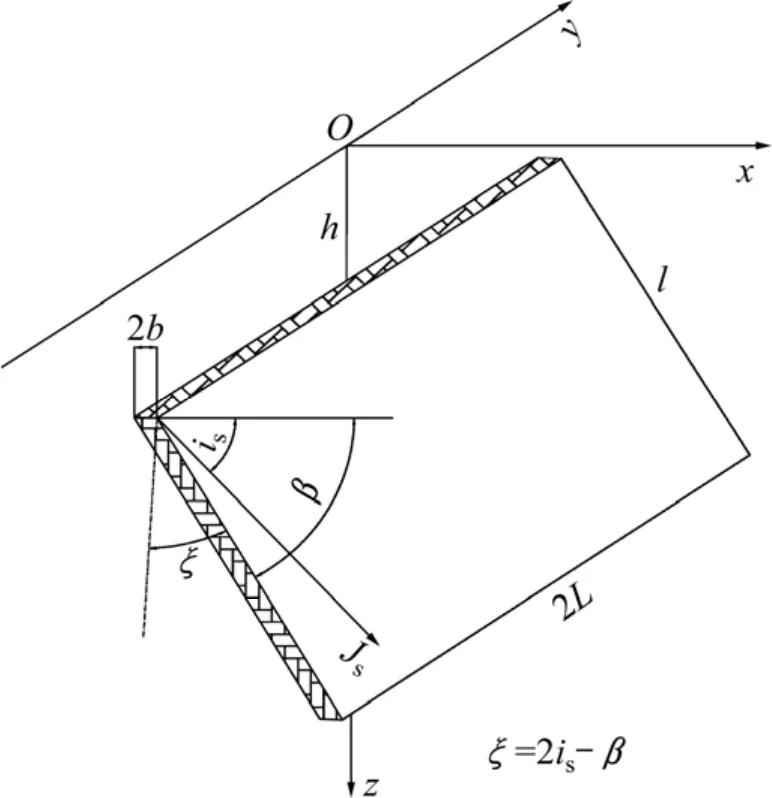
图1 薄板体几何及磁场要素图Fig.1 Thin body geometry and magnetic field elements

式(1)最初由Grant提出[13]，该公式对三度、似二度、二度异常均较适用，但由于在角度处理上存在问题，因而，一直未能得到推广使用。本文在利用此式前对相关错误进行纠正，并通过理论模型验算。本文提出的公式是修正后的公式。

2 共轭三角形建立及图形转换

磁异常共轭三角形及共轭元如图2所示。图2中曲线为单一板体磁异常曲线，异常包含了峰值区和谷值区2个主要部分。在图2中，线段AB和AV所在直线分别是通过峰值左翼拐点P1和右翼拐点P2的切线，线段VC所在直线是通过谷值区右翼拐点P3的切线，3条线段交汇构成一对底边平行，并以AV为公共边的三角形，这里称之为共轭三角形，其中三角形BAV与板体磁场峰值区对应，形象地称为“A型”三角形；三角形AVC与谷值区对应，形象地称为“V”型三角形，线段AV称为共轭边。三角形的高AU及VW将底边分成 BU，UV，AW 和 WC，显然，a，c，d和e这4个线段反映了共轭三角形的固有属性，也包含了丰富的磁异常信息，它们定义了一个完整的共轭三角形，这里称为共轭元。

根据式(1)一阶导数、二阶导数的数学意义[1]，可以计算出通过拐点P1，P2和P3的斜率k1，k2和k3及4个共轭元a，c，d和e。显然，共轭元是与板状体几何参数及磁场参数相关的初等函数，考虑到磁矩 Ms与磁化强度J及板体宽度b具有正比关系，共轭元的计算可以用通式表示为：

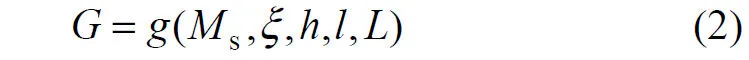
其中：g ∈(a,c,d,e)。

将G函数定义为共轭元函数，并把根据磁异常曲线求取共轭元函数的过程称为磁异常的图形转换。图形转换建立了共轭元与板体各要素 ),,,,(sLlhMξ 的函数关系，为异常特征信息直接进入反演过程奠定了理论基础。

通过式(1)求取一阶、二阶导数的过程是非常繁琐的过程，求解结果是一个相当复杂且包含板状体全部要素的五次方程，因而共轭元的精确解析非常复杂，必要时需借助数学工具，通过限定精度采取迭代法求解。

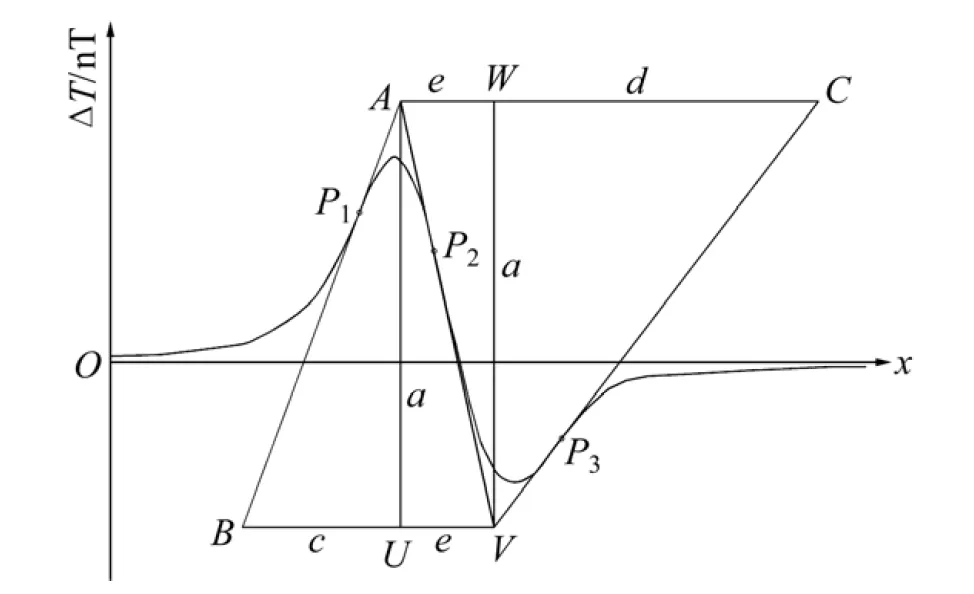
图2 磁异常共轭三角形及共轭元Fig.2 Magnetic anomaly conjugate triangle and conjugate element

3 共轭比值定义

下面定义2个比值：

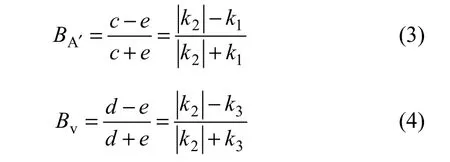
BA′和Bv反映了共轭三角形的畸异特性，包含了磁异常曲线的许多异常特征，定义为共轭比值。由于其计算过程实际上是共轭元函数的四则运算过程，因而，其计算通式可以表示为：

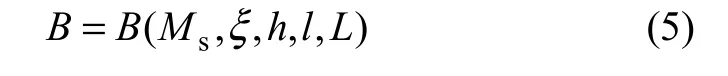
其中： B ∈ ( BA′,Bv)。

为了讨论问题方便，以BA′为纵轴，Bv为横轴定义一个共轭坐标系，数据对(BA′, Bv)称为共轭坐标。

在式(5)中，与板状体几何形态相关的参数为ξ，L和l，这3个参量也是影响磁场分布特征的关键因素，也往往是异常反演解释时的重要目标参量[14]。为了简化求解过程，需要设定初始条件，暂时将Ms和h看成常量，令其等于1个单位，而走向长度L也可以近似于异常走向长度 Cd，即令 L/h=Cd。简化后式(5)可以写成：

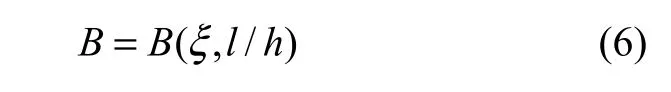
式(6)表明：在初始条件下，决定共轭坐标形态的参量只有2个。

设定边界条件如下：有效磁化倾角is=60°，L/h=3，讨论ξ和l/h变化时共轭坐标轨迹的一些特征。

首先分别令 l/h为 0.5，1.0，1.5，2.0，2.5，3.0和3.5，连续变化ξ，通过搜索得到的共轭坐标轨迹是一系列封闭或近似封闭的曲线，即图3中虚线，形象地称为共轭纬线。

同理，分别令ξ等于某一固定值，连续变化l/h，则搜索得到的共轭坐标轨迹是一系列向外发散的放射状曲线，即图3中实线，形象地称为共轭经线。

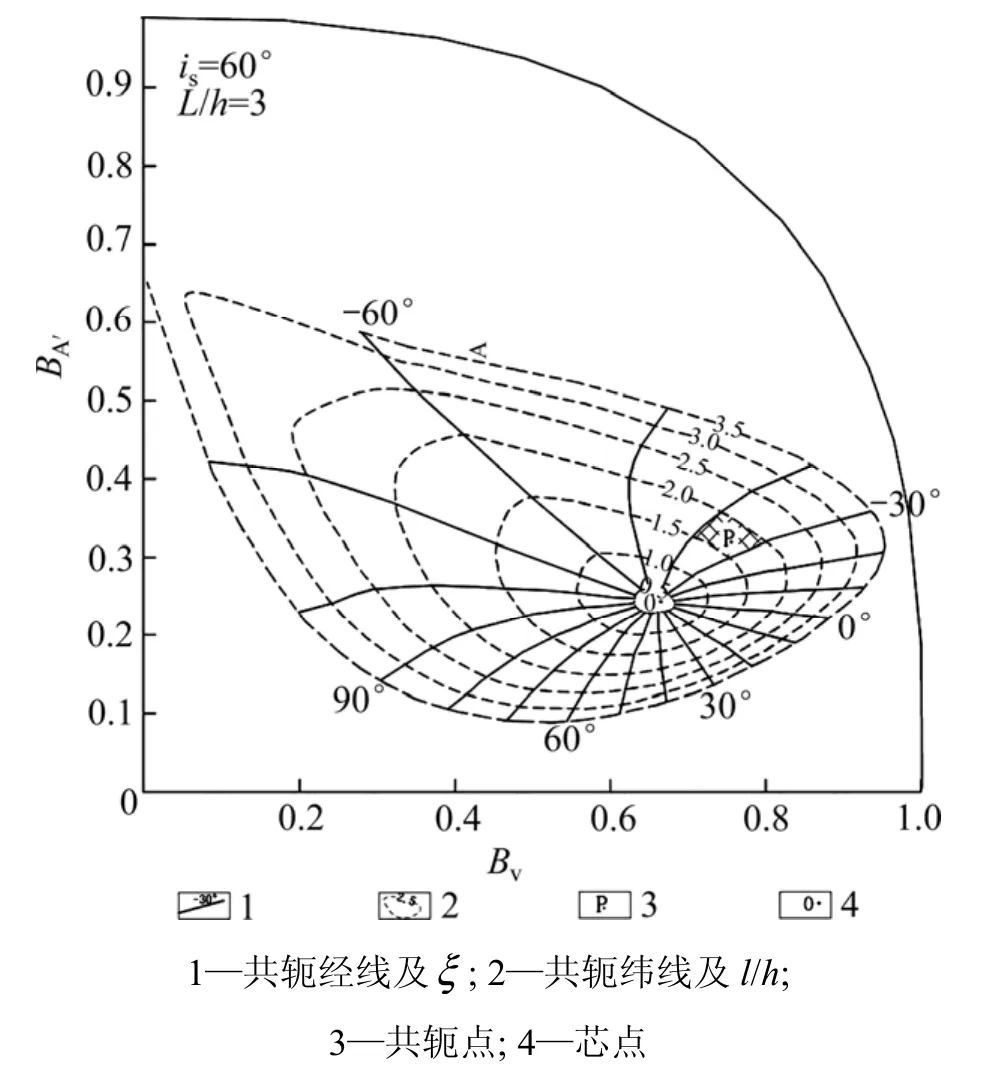
图3 ΔT磁异常共轭网络Fig.3 Magnetic anomaly conjugate network diagram

图3 中经线与纬线组成了一个网状图形，称为共轭网络图。搜索网络中的点(例如点P)或某个网格块可以初步确定板状体倾角、下延长度等参数值或其变化范围。

因而，一个异常的2个共轭比值A′B和Bv，在分别以A′B和Bv为纵、横坐标的共轭坐标系中形成一个共轭点。无数边界条件相同的共轭点以变化磁性体倾角的共轭点轨迹形成共轭纬线；变化磁性体下延长度的共轭点轨迹形成共轭经线；并以倾角为0°、下延长度近似为0的共轭点为共轭“芯点”。一定边界条件的共轭坐标、经纬线、芯点组成一幅形似蓓蕾的“共轭网络图”。

边界条件确定的共轭点在共轭网络中具有唯一性。这是最重要的性质。利用这一性质，通过坐标逐步搜索，即可优先精确地解出ξ与l/h这2个参数，其中ξ是最重要的关键参数。ξ被优先得出，是采用共轭元突破磁异常全参量解释的重要贡献。

4 磁异常共轭元反演解释

基于共轭元求取磁异常磁源体几何、磁性参数的过程简称为磁异常的共轭元反演解释。一个完整异常的共轭元反演解释由共轭解释与校正解释 2部分组成，解释过程可由程序根据异常的特征参数自动完成。

4.1 共轭解释

在实际应用中，通过几何作图法或曲线拐点追踪算法[14]求出实测磁异常的共轭元，利用式(3)和(4)计算共轭坐标点(A′B, Bv)。然后利用式(6)，不断变化板状体要素ξ和l/h求取共轭点，通过多次迭代，可以使求取的共轭点逼近实测的共轭点(A′B, Bv)。当满足设定条件时，可以将ξ和l/h作为最终结果。因此，共轭元反演解释过程实际上包括2个主要环节，即图形变换与变换图形。变换图形是指逐步变换共轭三角形的图形，在相同边界条件的共轭网络图中，搜索到由实测异常确定的共轭点的位置。在解释过程中，每一个共轭点都是通过设定参数去计算异常，并经图形变换为共轭三角形后计算获得。因此，实测异常确定的共轭点与解释过程中的共轭点之间的本质差异是：前者虽包容了实测异常中的重要信息，但全部是未知的；后者在解释过程中虽与实测异常暂无关系，但其异常中的所有参数均是具体的。在几何上可以证明：当2点重合后，实测异常的共轭三角形与解释异常的共轭三角形为相似三角形。在实测异常与解释异常共轭点重合时，根据相似原理变未知为已知，则可解出异常体的全部未知参数。下面对这一过程进一步说明。

当共轭点确定后，据共轭经线坐标得出ξ，据共轭纬线坐标得出l/h。该过程完成时，相当于在共轭解释子程序中，建立了一个以磁体上顶埋深、磁矩为单位(都等于1)的“相似共轭三角形”。

由图形变换得到的共轭三角形，其中有关磁性体的参数是完全未知的。而相似共轭三角形中除优先解出ξ和lt/h外(由于前述l非最终值，暂令lt=l)，还可以给出：

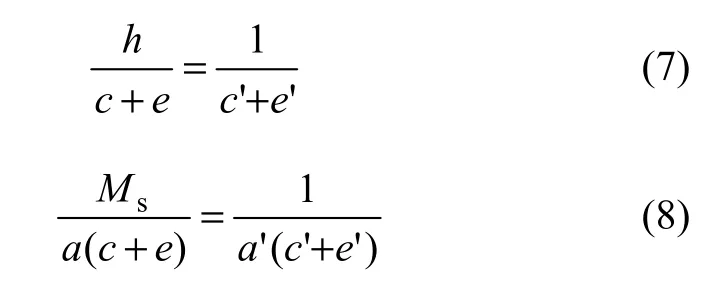
因此，利用共轭三角形与相似共轭三角形中对应参数的等比性质，并令M (ξ)=，则有：

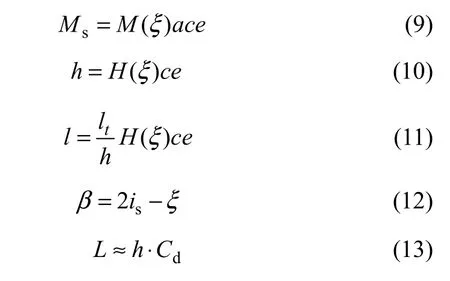
式(9)～(12)分别是共轭法求解磁矩、磁性体上顶埋深、下延长度、倾角的定量解释公式；式(13)是磁性体半长度的半定量解释公式，其中，Cd为异常走向长度，是L/h的近似数。

定量解释实测异常时，还有2个公式也相当重要：

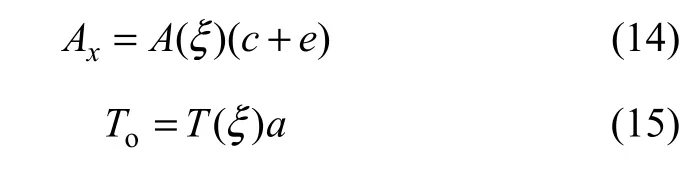
式(14)和(15)分别是异常的原点、正常场定量解释公式。其中：Ax是共轭三角形顶点与磁性体上顶中心在地表投影点间的横坐标；To是共轭三角形顶点至正常场间的纵坐标。同样，A(ξ)和T ( ξ)是以ξ为变量的函系数。T(ξ)等所有函系数均是某一常量的倒数，因此，磁性体有关参数的求解均十分简便。

4.2 校正解释

校正解释是指异常经剖面解释后，为校除因“近似数Cd”给解释结果带来的误差，根据磁异常平面特征参数，校正用于剖面解释中的L/h代数值，进而完善解释结果的过程。

地磁倾角以及异常体走向半长度与埋深之比(L/h)是共轭解释的2个不可或缺的边界条件。但在共轭元解释过程中，L/h选用数值十分相近Cd参数代替。因此，解释结果存在误差。

校正解释中涉及的参数都是与异常平面特征有关的特征参数见图4。

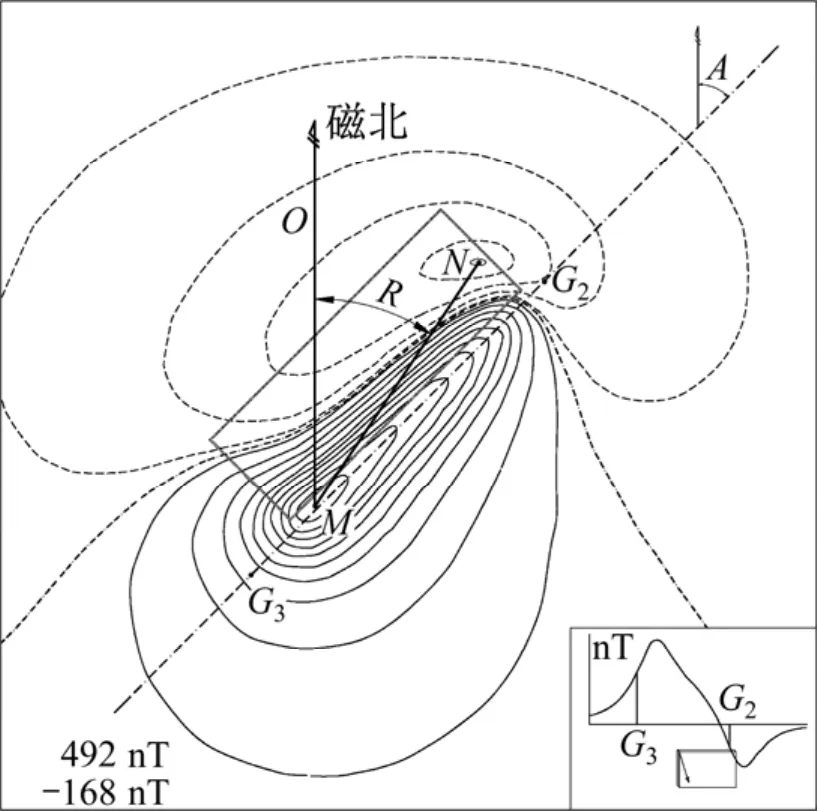
图4 异常平面特征点及要素Fig.4 Abnormal plane feature point and factor

图4 中：GMN为极值距，指异常平面图中的极值间距；R为极线角，是极值连线与磁北之间的夹角；G23为长轴拐点距，为异常平面图中异常长轴上拐点之间的坐标量；为正负异常极值点距离。

图4中：GMN=；R=∠OMN； G23= G2-G3。

当异常长轴方位角A＜45°时，GMN与2L之间在量值上有近似相等的关系；当异常长轴方位角A＞45°时，G23与2L之间，在量值上有近似相等的关系。因此，选择了GMN与LG作为长深比Cd的代数。

当-45°＜A＜45°时，

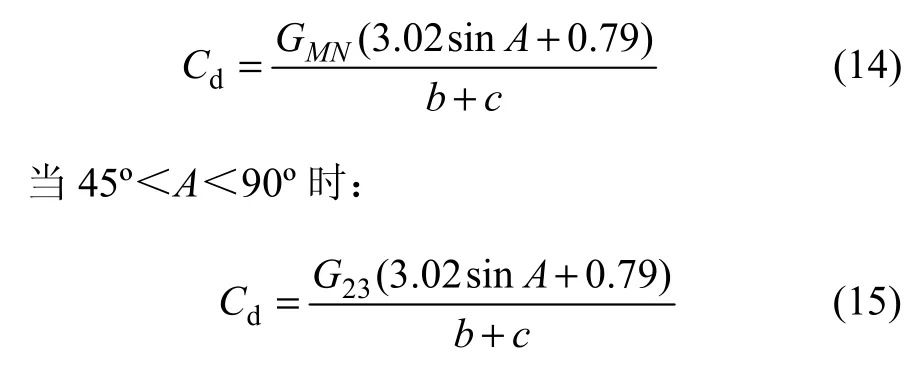
在一般情况下，Cd与L/h具有较高的近似程度。倘若长深比Cd等于L/h，则剖面解释阶段即会得到精确的解释结果，绘制的解释结果平面等值线图必定与给定异常平面等值线图完全一致。同时，解释结果的剖面曲线与给定异常剖面曲线之间也会高度拟合；假若Cd小于或大于L/h，则解释结果平面等值线图的长轴会明显减短或加长，同时解释结果剖面曲线与给定异常剖面曲线之间拟合后会出现明显的剩余异常。可见，解释结果的误差主要来源于Cd。因此，校正解释过程是校正Cd的过程。

校正解释是在完成共轭解释基础上进行的。校正有2种途径：

(1) 利用共轭解释前、后异常平面图中的“极间距”与“极线角”差异完成校正。

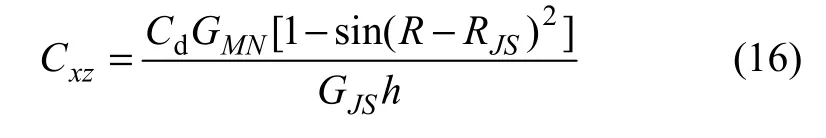
(2) 利用共轭解释前、后异常平面图中的“极间距”与“长轴拐点距”比值完成校正。

当-45°＜A＜45°时：

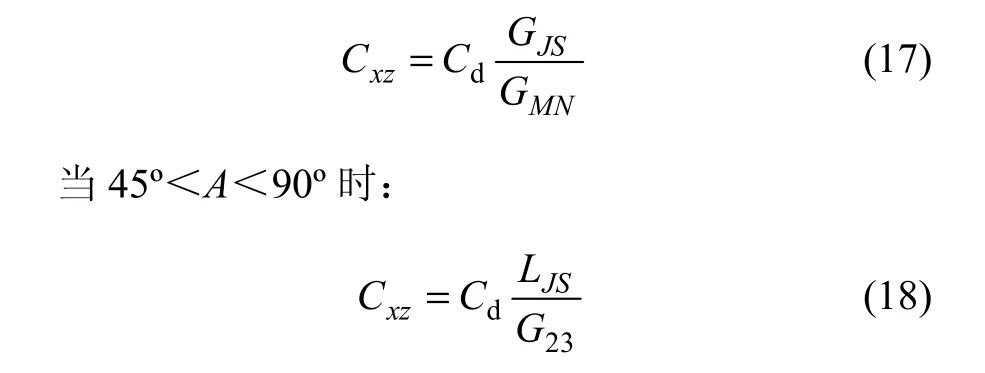
式中：Cxz，CJS和LJS分别为长深比代数校正值、解释结果平面异常的极间距、解释结果平面异常的长轴拐点间距。

采用式(16)对一模型异常进行反演计算，其模型参数、共轭解释结果、校正结果及校正误差见表 1，可见：通过校正解释后，解释结果相对误差不大于1%，6个模型参数均得到了精确解释结果。

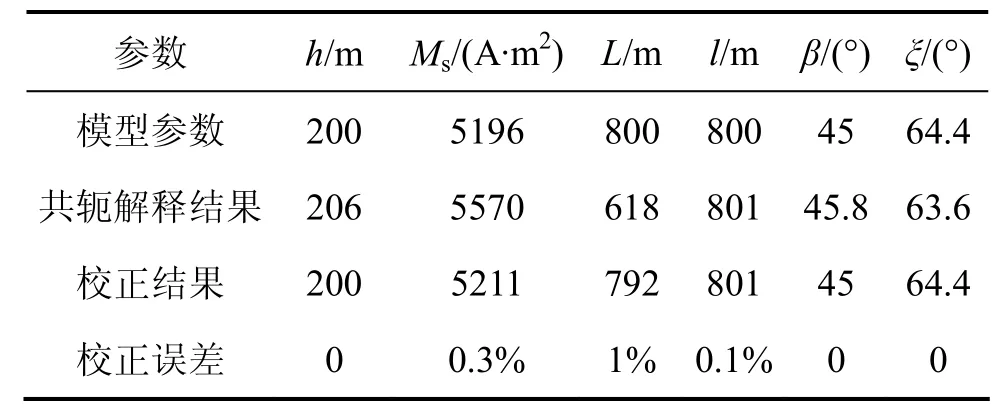
表1 理论模型磁异常共轭元反演解释过程参数表Table1 Theoretical model of magnetic anomaly conjugate element inverse interpretation process parameter

实践中，给定异常的参数都是未知的，解释结果中不可能给出模型参数误差水平；因此，可靠性的鉴别要靠异常剖面的拟合与平面图的比照完成。

当异常剖面拟合后出现明显剩余异常时，表明尚未得到最佳解释结果，这是ΔT磁异常共轭解释法的剖面判别；当进行平面图异常比照后，如果异常形态基本一致，但展布面积与异常极值有明显差异，亦表明尚未得到最佳解释结果，这是ΔT磁异常共轭元解释法的平面鉴别。通过剖面判别与平面鉴别，采用ΔT磁异常共轭解释法均可得到相对精确而可信的解释结果。

5 实例

共轭元反演在广东省、湖南省、青海省得到多次应用，均取得了较好的应用效果。现以广东某铁矿[15]为例，阐明其应用过程与效果。

区内地磁倾角为34.4°，异常圈定基本完整(图5)。异常的长短轴比值约为3.5。利用N44线磁异常进行共轭元反演解释。异常曲线总体具有单体异常的曲线特征，但经过逐步解释后发现，异常由3个磁性体叠加引起。其解释结果如表2及图5所示。

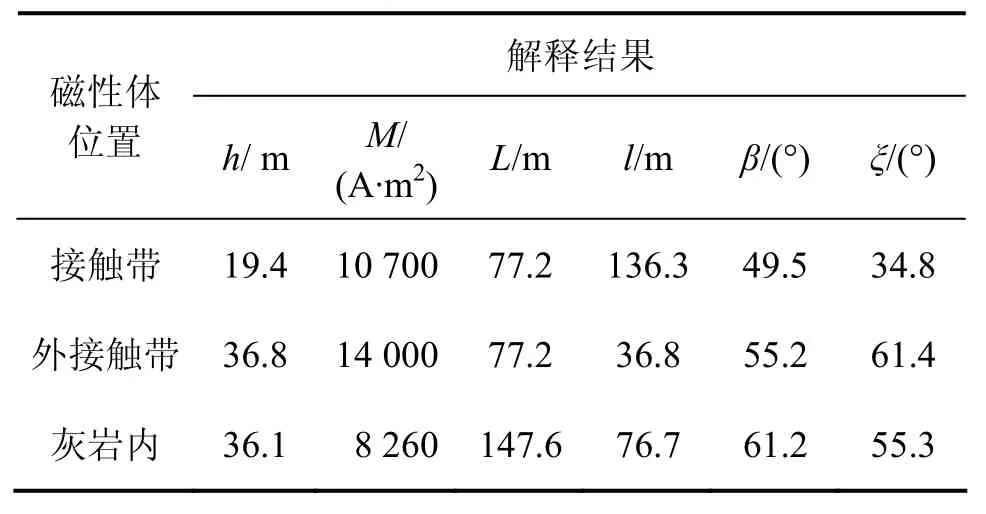
表2 广东某磁铁矿N44线磁异常共轭元反演解释结果Table2 A magnetite magnetic anomaly conjugate element inverse interpretation results for Line44

表2中，接触带指灰岩与花岗岩接触部位。剖面解释结果表明：实测磁异常与反演结果模型磁异常的平面图及剖面图展示的异常形态、展布范围、幅值特征基本吻合；钻孔见矿深度与反演模型通过部位基本吻合，解释结果得到的外接触带磁性体磁性强度更高且无钻孔控制，为盲矿体的可能性大。实例反演结果较充分地体现了共轭元反演解释方法的实用性、可靠性及在异常识别、异常分解等方面的优越性。

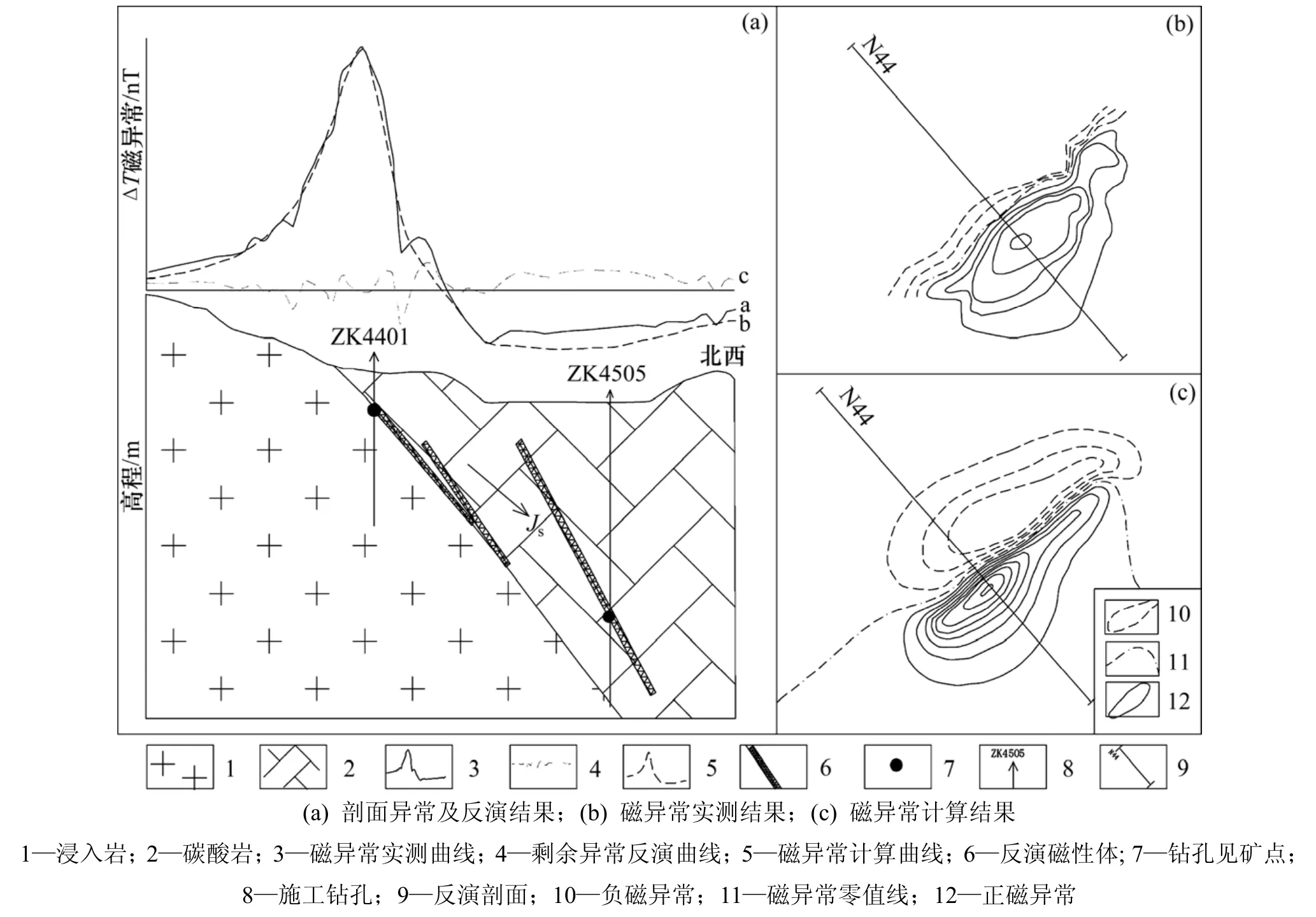
图5 广东某磁铁矿磁异常共轭元反演解释结果Fig.5 Magnetite magnetic anomaly conjugate element inverse interpretation results

6 结论

(1) 共轭元反演解释是通过提取磁异常剖面特征和平面特征实现磁异常的图形转换，在解释过程中不断细化对异常特征的认识，最后得出磁性体几何参数和磁场参数的反演方法。

(2) 在解释过程中考虑了磁异常平面信息，但又不完全依赖于平面信息的完整程度，该方法在提高解释结果可靠性的同时，较大限度地放宽了方法的应用条件。在反演过程中没有复杂的数学运算和大型方程的求解，可以大大提高反演效率，减少反演期间的累加误差。

(3) 虽然该方法是建立在薄板体磁异常的基础之上，但由于该方法同样满足迭加原理，因而可以通过不同特征薄板体的迭加实现诸如二度体、三度体等模型体的反演。该方法具有较大的研究空间和广阔的应用前景。模型试算和实例结果表明：其解释结果具有较高的精度和可靠性。

[1] 安玉林, 谭保华. 局部重磁场源全方位成像[M]. 北京: 地质出版社, 1997: 3-16.

AN Yu-lin, TAN Bao-hua. Omnidirectional imagery of local gravity and magnetic anomaly sources[M]. Beijing: Geological Press, 1997: 3-16.

[2] 管志宁. 地磁场与磁法勘探[M]. 北京: 地质出版社, 2005:85-160.

GUAN Zhi-ning. Geomagnetic field and magnetic exploration[M]. Beijing: Geological Press, 2005: 85-160.

[3] 刘天佑. 位场勘探数据处理新方法[M]. 北京: 科学出版社,2007: 1-85.

LIU Tian-you. New data processing methods for potential field exploration[M]. Beijing: Science Press, 2007: 1-85.

[4] 刘天佑. 重磁异常反演理论与方法[M]. 北京: 中国地质大学出版社, 1992: 19-88.

LIU Tian-you. The theory and method on inversion of gravity and magnetic anomalies[M]. Beijing: The Press of China University of Geosciences, 1992: 19-88.

[5] John A. Introductory geophysical inverse theory[M]. Colorado:Samizdat Press, 2001: 183-185.

[6] Snieder R. An extension of Backus-Gilbert theory to nonlinear inverse problems[J]. Inverse Problems, 1991(7): 409-433.

[7] 赵改善. 求解非线性最优化问题的遗传算法[J]. 地球物理学进展, 1992, 7(1): 90-97.

ZHAO Gai-shan. Nonlinear optimization using genetic algorithms[J]. Progress in Geophysics, 1992, 7(1): 90-97.

[8] Raiche A. A pattern recognitionapproach to geophysical inversion using neural nets[J]. Geophysics J Int, 1991, 105(3):629-648.

[9] Tarantola A. Inverse problem theory and methods for model parameter estimation[M]. The Society for Industrial and Applied Mathematics, 2005: 1-40.

[10] Anderssen R S, Seneta E. Asimple statistical estimation procedure for Monte-Carlo inversion in geophysics[J]. Pure Appl Geophys, 1971, 96(1): 5-14.

[11] Nabighian M N. Toward a tree-dimensional automatic interpretation of potential field data via generalized Hilbert transforms: Fundamental relations[J]. Geophysics, 1984, 49(6):780-786.

[12] 刘天佑. 地球物理勘探概论[M]. 北京: 地质出版社, 2007:122-124.

LIU Tian-you. Conspectuss of geophysical exploration[M].Beijing: Geological Press, 2007: 122-124.

[13] Grant F S. Interpretation theory applied geoghysics[M]. US: Mc Graw-Hill Book Company, 1965: 307-354.

[14] Nabighian N N. The analytic signal of two-dimensional magnetic bodies with polygonal cross-section[J]. Geophysics,1972, 37(3): 507-517.

[15] 伍卓鹤, 何俊美. 粤中-粤东地区区域重力成果[J]. 物探与化探, 2007, 31(5): 435-439.

WU Zhuo-he, HE Jun-mei. Achievements of regional gravity survey in central and eastern Guangdong Province[J].Geophysical and Geochemical Exploration, 2007, 31(5):435-439.