刚性挡墙主动破坏墙后土拱效应细观研究

彭述权，李夕兵，樊 玲

(中南大学 资源与安全工程学院，湖南 长沙，410083)

土拱效应是岩土工程中的一种常见现象。Terzaghi等[1]认为土拱效应是一部分土体与其余部分发生相对位移运动，导致该部分土体压力减小、相邻土体压力增加的现象。Fang等[2-3]通过挡墙模型试验分析得出刚性挡墙墙体运动会导致墙后土体内产生土拱效应。土拱效应是导致刚性挡墙绕墙顶转动墙后土压力呈非线性分布的1个重要原因，使得土压力合力作用点上移，降低挡墙的稳定性。Huang等[4-6]通过对挡墙绕墙顶转动位移模式研究，认为挡墙绕墙顶转动土压力与其他位移模式有很大不同。由于试验技术条件所限，以上研究并没有给出墙后土拱效应特征的任何测量结果。目前，考虑土拱效应挡墙土压力计算分析是挡墙土压力理论研究的热点。Handy等[7]提出主应力旋转而导致土拱效应，假定土拱曲线为悬链线；Park[8]提出圆弧曲线法分析土拱曲线； 彭述权等[9]提出抛物线法分析土拱曲线，并且归纳土拱曲线可为二次曲线；李永刚等[10-11]将此理论进行拓展，将其用于挡墙后土压力计算，认为土拱效应导致刚性挡墙后土压力非线性分布；墙土摩擦角和土体摩擦角越大，土拱效应越显著；吴子树等[12-13]推断了土拱效应的形成条件。目前，土工效应形成机理尚不清楚，在其应用过程中，没有考虑土拱效应适用条件，笼统地将土拱效应用于任何挡墙位移模式的土压力分析，导致与试验结果相矛盾[2]，因而，有必要深入研究土拱效应形成机理，分析其与挡墙土压力非线性分布之间的关系，进而完善考虑土拱效应挡墙土压力计算方法。颗粒流理论(PFC2D)是由 Cundall等[14]提出的一种基于离散元理论数值模拟方法，是一种适合土体等散粒体细观模拟的方法。周健等[15]利用颗粒流方法模拟刚性挡墙主动土压力和被动土压力；彭述权[16]将刚性挡墙后土体看作土颗粒聚合体，应用颗粒流方法研究挡墙和重力作用下土颗粒位置和其间接触力变化规律，揭示挡墙后土体细观破坏机理，研究表明：细观颗粒流方法是一种研究挡墙土拱效应细观机理的可行方法。基于以上分析，本文作者建立刚性挡墙颗粒流模型，运用颗粒流方法研究刚性挡墙后土拱效应细观形成机理，提出跨高比和矢高比表征细观土拱曲线，得到刚性挡墙墙后土拱效应的形成条件；进一步分析土颗粒和墙土摩擦因素、挡墙位移、土颗粒刚度对土拱效应影响规律。

图1 刚性挡墙PFC数值模拟图Fig.1 PFC2D numerical simulation of rigid retaining wall

1 绕墙顶转动墙后主动土压力细观颗粒流模拟

首先，采用颗粒流方法模拟刚性挡墙绕墙顶转动主动土压力分布，与试验结果[2]进行对比分析，验证颗粒流方法模拟土拱效应的可行性。

模型箱高为0.70 m，宽为1.20 m，在自重作用下，平衡后土体高为0.50 m。模型箱左侧由2段墙体组成，下段长为0.05 m，上段长为0.65 m，见图1。颗粒本构模型采用滑动连接模型，颗粒生成参数见表 1。滑动连接模型的颗粒之间或颗粒与墙体之间的接触力和颗粒位移呈线性关系；颗粒之间或颗粒与墙体之间的连接刚度由颗粒刚度或墙体刚度并联而成；颗粒之间或颗粒与墙体之间存在摩擦因素，颗粒之间的切向力与法向力之比小于或等于摩擦因素，即

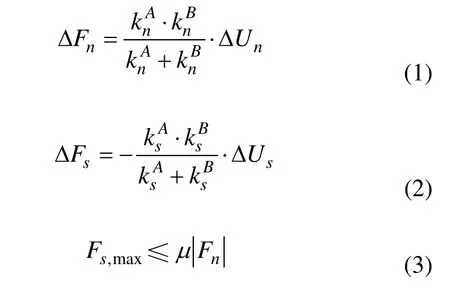
式中：Fn和Fs分别为颗粒间或颗粒与墙体间的法向力和切向力；ΔUn和ΔUs分别为颗粒间法向位移和切向位移；分别为颗粒A的法向接触刚度和切向刚度；分别为颗粒B的法向接触刚度和切向刚度；µ为颗粒摩擦因素或墙体摩擦因素。

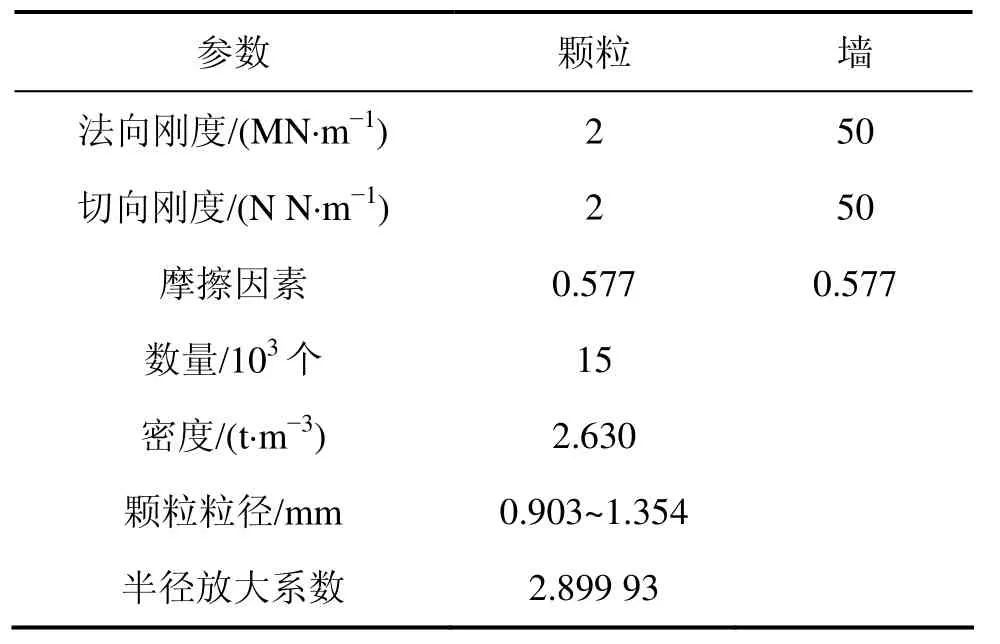
表1 刚性挡墙模型参数Table1 Parameters of retaining wall model

刚性挡墙PFC模型建立步骤如下。

(1) 用墙体建立模型箱，在其内随机生成15 000个颗粒，初始孔隙度为0.9，按表1设定墙体和颗粒刚度、摩擦因素。重力加速度设为10 m·s-2。

(2) 采用扩大颗粒半径方法逐步增大颗粒半径，直到满足颗粒孔隙度为0.16为止。

(3) 施加竖向重力加速度9.81 m·s-2，重新设定摩擦因素，使颗粒体在自重作用下重新平衡生成试样，如图1所示。

图 2(a)所示为挡墙绕墙顶转动主动土压力分布呈模拟结果，刚性挡墙的速度经试算平转动角速度为1.5×10-5rad·s-1；挡墙土压力通过测量圈获得，测量圈半径为颗粒平均半径的6倍。由图2(a)可见：当墙体底部位移为0.016H(H为墙高)时，挡墙主动土压力显著非线性分布。

图 2(b)所示为Fang等[2]提出的挡墙绕墙顶转动土压力分布模型试验测量结果。其中：填土高度为0.50 m；密度为1.550 t/m3；smax为挡墙底部处水平位移。由图 2(a)和图 2(b)可知：颗粒流模拟结果和模型试验结果基本吻合，说明颗粒流模拟刚性挡墙土压力分布是可行性的，模拟刚性挡墙后土拱效应具有可行性。

图2 绕墙顶转动土压力颗粒流模拟结果与实测结果比较Fig.2 Comparison of active earth pressure with rigid retaining wall movement model of RT by PFC2D and experiment

2 墙后土拱效应细观颗粒流模拟

2.1 挡墙绕墙顶转动土拱曲线模拟

土拱效应细观解释如下：土颗粒不均匀位移形成挡墙后土拱曲线，刚性挡墙后土拱曲线为向上开口的曲线。

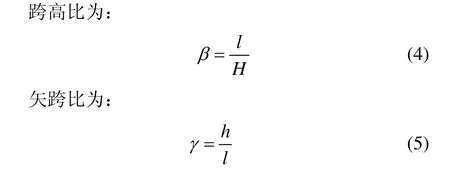
式中：l为土拱曲线跨度；h为土拱曲线最大高度；H为挡墙后土颗粒的高度。土拱曲线的跨高比和矢跨比表明土拱曲线弯曲程度。土拱曲线跨高比和矢跨比越大，土拱效应越明显；反之，土拱效应不显著。

图3所示为土体不同水平高度处颗粒竖向位移，对应挡墙最大水平位移为20 mm。距墙顶部0.4H范围内水平位置颗粒竖向位移成勺型，形成土拱曲线；位于 0.4H到墙底部水平范围土颗粒竖向位移随到挡墙水平距离增大而单调减小，土拱曲线逐渐不明显。土拱效应形成区域是沿着挡墙高度特定范围内形成，而不是沿墙高均匀形成。取土拱曲线对称部分，跨度约为0.12 m，跨高比约为0.24，土颗粒最大位移约为0.80 mm，土拱曲线最大高度为0.80 mm，矢跨比为0.68%。

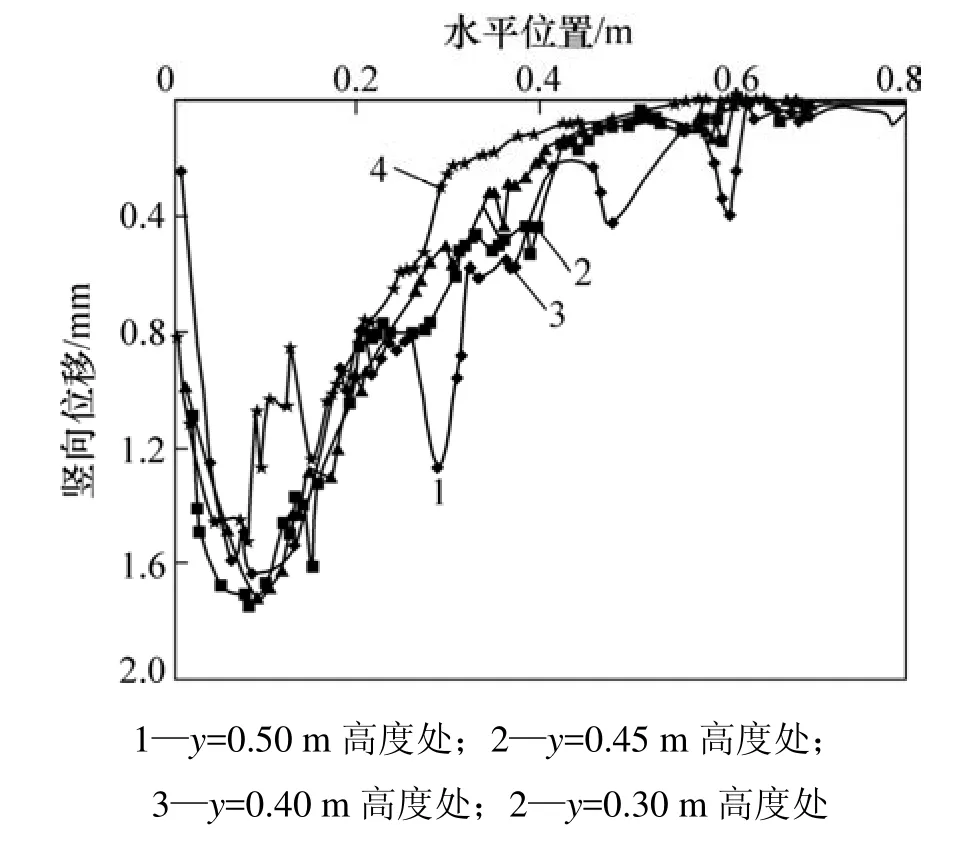
图3 挡墙绕墙顶转动竖向位移Fig.3 Vertical displacements of particles with rigid retaining wall movement model of RT

图4 和图5所示分别为挡墙绕墙顶转动不同挡墙位移土颗粒竖向位移和颗粒接触力分布，对应挡墙0.3H处。从图4和图5可见：当挡墙位移为10 mm，相对位移为0.02H时，同一高度处竖向位移呈明显勺型，靠近挡墙部位土体内部细观接触力分布发生明显旋转，接触力主方向不再是竖向方向，而是接近水平方向，此时，土压力已经达到主动土压力状态，土拱效应尚未消失；而当挡墙位移增大到25 mm，相对位移为0.05H时，挡墙土拱效应不再明显。

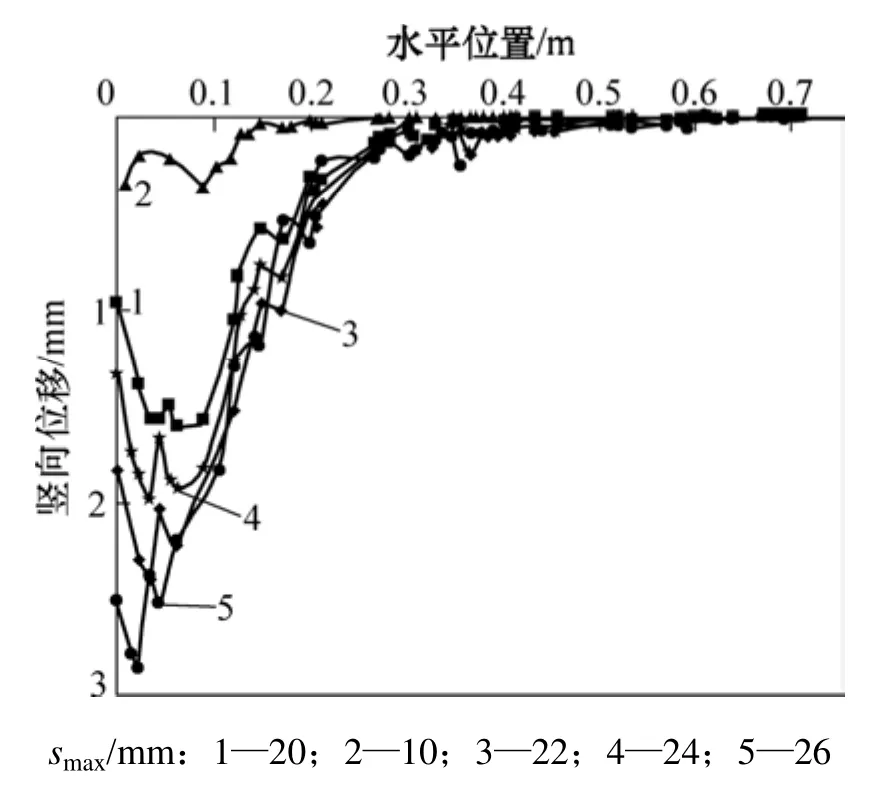
图4 不同挡墙位移时的颗粒竖向位移Fig.4 Vertical displacements of particles with different displacements

图5 不同挡墙位移的颗粒接触力分布Fig.5 Distribution of particle’s contact force with different displacements

2.2 不同位移模式对土拱效应影响

图6 所示为挡墙平移和绕墙底部转动墙后水平位置土颗粒竖向位移。从图6可知：两者竖向位移均单调减小，没有形成明显土拱效应；对应刚性挡墙位移均为20 mm，相对位移为0.04H，颗粒摩擦因素和墙体摩擦因素均为0.577。结合图3和图6可知：土拱效应显著地受到挡墙位移模式的影响，挡墙绕墙顶转动情况下土拱效应明显，挡墙平移、挡墙绕墙底部转动情况下土拱效应不明显。因此，考虑土拱效应研究挡墙土压力理论时，要充分考虑不同挡墙位移模式对土拱效应的影响。

2.3 不同摩擦因素和颗粒刚度对土拱效应的影响

图7和图8所示分别为不同摩擦因素和颗粒刚度的挡墙后土颗粒竖向位移，其对应位移模式是绕墙顶部转动，挡墙位移为0.04H，颗粒位于挡墙0.2H高度处。从图7可见：在一定范围内，颗粒明摩擦因素越大，土拱效应较明显；当颗粒摩擦因素为0时，墙后土拱曲线不再是规整的曲线，土拱效应不再明显。颗粒刚度包括法向刚度和切向刚度，本次模拟中法向刚度和切向刚度保持相同比例，分析土颗粒法向刚度变化对土拱曲线影响规律。从图8可知：土颗粒刚度越小，土拱曲线的跨度和高度越大，土拱效应越明显。

图6 不同位移模式的颗粒竖向位移Fig.6 Vertical displacements of particles with different retaining wall movement models

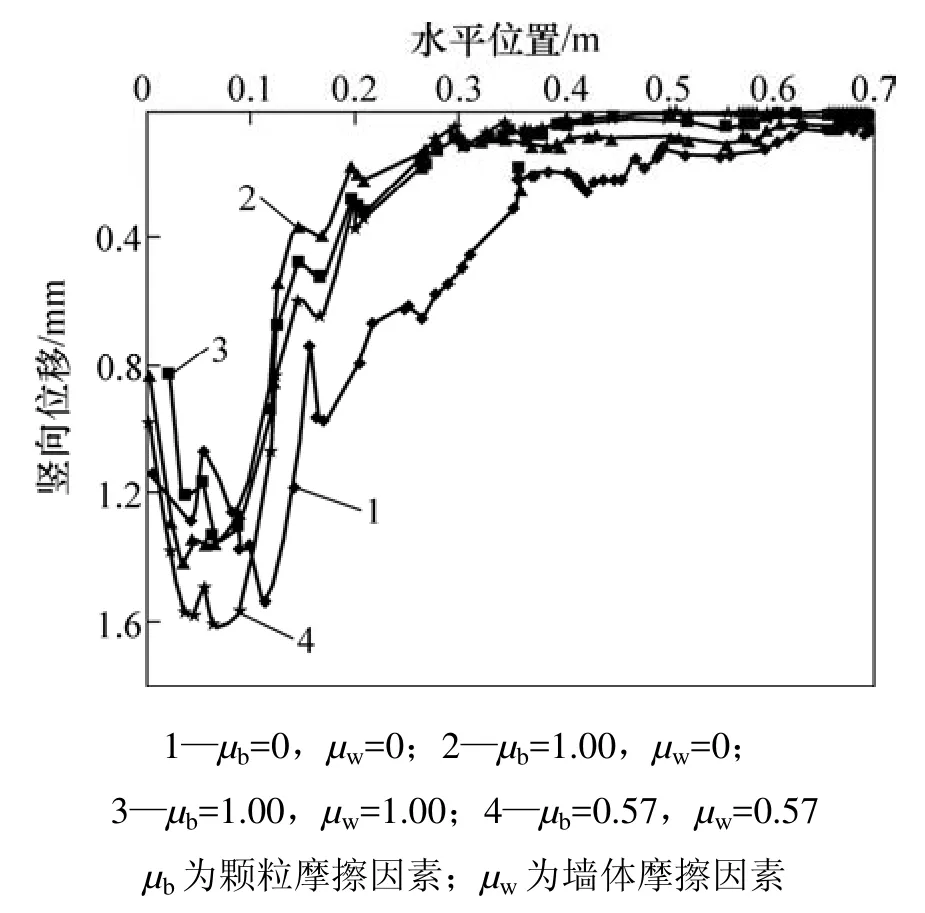
图7 不同摩擦因素的颗粒竖向位移图Fig.7 Vertical displacements of particles with different frictional coefficients

图8 不同颗粒刚度颗粒竖向位移图Fig.8 Vertical displacements of particles with different shiftnesses

在挡墙绕墙顶转动位移模式情况下，将挡墙位移、颗粒和墙体刚度摩擦因素和颗粒刚度三因素的相对比值作为横坐标，土拱曲线的跨高比和矢高比作为纵坐标，得到土拱效应影响因素(颗粒粒度比、摩擦因素比、位移比)综合评价结果，见图9。从图9可知：随着颗粒摩擦因素增大，土拱曲线矢高比、跨高比均增大，土拱效应越明显，且土拱效应受颗粒刚度和挡墙位移影响最大，颗粒摩擦因素影响较小。采用细观颗粒流模拟土拱曲线以及绕墙顶转动刚性挡墙主动土压力分布，与相应主动土压力实测结果较吻合。细观颗粒流模拟结果较好地模拟了墙后土拱效应形成机理以及挡墙位移、颗粒摩擦因素和刚度等细观参数对土拱效应的影响规律。研究结果对更深入研究考虑土拱效应挡墙土压力理论具有重要意义。

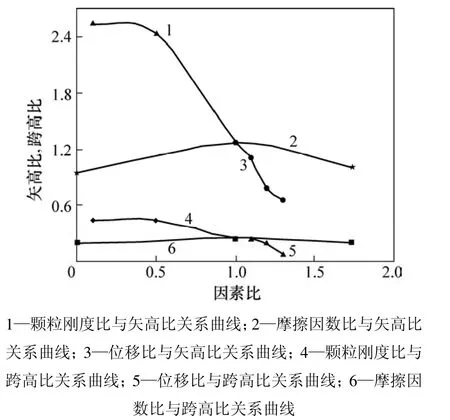
图9 土拱效应影响因素分析Fig.9 Analysis of influencing factors on soil arching

3 结论

(1) 细观颗粒流方法能较好地模拟刚性挡土拱效应的细观机理和绕墙顶转动主动土压力分布，对深入研究考虑土拱效应挡墙土压力理论具有一定的理论价值。

(2) 在刚性挡墙主动破坏过程中，当刚性挡墙绕墙顶转动位移小于0.05H时，沿墙高距墙顶0.4H范围内土拱效应显著，其他挡墙位移模式土拱效应不明显，计算挡墙绕墙顶转动主动土压力时应考虑土拱效应影响。

(3) 刚性挡墙主动破坏墙后土拱效应受挡墙位移模式和颗粒刚度的影响较大，受颗粒和墙体摩擦因素的影响较小。

[1] Terzaghi A. 理论土力学 [M]. 徐志英, 译. 北京: 地质出版社, 1960: 20-50.

Terzaghi A. Theory mechanics of soil[M]. XU Zhi-ying, trans.Beijing: Geology Press, 1960: 20-50.

[2] Fang Y S, Ishibashi I. Static earth pressure with various wall movement[J]. Journal of Geotechnical Engineering, 1986, 112(3):317-333.

[3] 周应英, 任美龙. 刚性挡墙主动土压力的试验研究[J]. 岩土工程学报, 1990, 12(2): 19-26.

ZHOU Ying-ying, REN Mei-long. An experimental study on active earth pressure behind rigid retaining wall[J]. Chinese Journal of Geotechnical Engineering, 1990, 12(2): 19-26.

[4] Huang C C, Menq F Y. The effect of the bending rigidity of a wall on lateral pressure distribution[J]. Canadian Geotechnical,1998, 36(6): 1039-1055.

[5] Chang M F. Lateral earth pressure behind rotating walls[J].Canadian Geotechnical Journal, 1997, 34(2): 498-509.

[6] 龚慈, 魏纲, 徐日庆. RT模式下刚性挡墙土压力计算方法研究[J]. 岩土力学, 2006, 27(9): 1588-1592.

GONG Ci, WEI Gang, XU Ri-qing. Earth pressure against rigid retaining wall rotating about top[J]. Rock and Soil Mechanics,2006, 27(9): 1588-1592.

[7] Handy R L. The arch in soil arching[J]. Journal of Geotechnical Engineering, 1985, 111(3): 302-318.

[8] Park K H. Estimation of active earth pressure against rigid retaining wall considering arching effect[J]. Geotechnique, 2003,53(7): 643-653.

[9] 彭述权, 周健, 樊玲, 等. 考虑土拱效应绕墙顶转动刚性挡墙土压力分布[J]. 岩土力学, 2008, 29(10): 2701-2707.

PENG Shu-quan, ZHOU Jian, FAN Ling，et al. Distribution of earth pressure of retaining wall with wall movement of rotation about top considering soil arching[J]. Rock and Soil Mechanics,2008, 29(10): 2701-2707.

[10] 李永刚, 白鸿莉. 垂直墙背挡土墙土压力分布研究[J]. 水利学报, 2003, 2: 102-106.

LI Yong-gang, BAI Hong-Li. Study of earth pressure distribution on the retaining wall with vertical back[J]. Shui Li Xue Bao,2003, 2: 102-106.

[11] 蒋波, 应宏伟, 谢康和. 挡土墙后土体拱效应分析[J]. 浙江大学学报: 工学版, 2005, 39(1): 131-136.

JIANG Bo, YING Hong-wei, XIE Kang-he. Analysis on soil arching behind retaining wall[J]. Journal of Zhejiang University:Engineering Science, 2005, 39(1): 131-136.

[12] 吴子树, 张利明, 胡定. 土拱的形成机理及存在条件的探讨[J]. 成都科技大学学报, 1995, 83(2): 15-19.

WU Zi-shu, ZHANG Li-ming, HU Ding. Studies on the mechanism of arching action in loess[J]. Journal of Chengdu University of Science and Technology, 1995, 83(2): 15-19.

[13] 贾海莉, 王成华, 李江洪. 关于土拱效应的几个问题[J]. 西南交通大学学报, 2003, 38(4): 398-402.

JIA Hai-li, WANG Cheng-hua, LI Jiang-hong. Discussion on some issues in theory of soil arch[J]. Journal of Southwest Jiaotong University, 2003, 38(4): 398-402.

[14] Cundall P A, Strack O D L. A discrete numerical model for granular assembles[J]. Geotechnique, 1979, 29(1): 47-65.

[15] 周健, 彭述权, 樊玲. 刚性挡土墙主动土压力颗粒流模拟[J].岩土力学, 2008, 29(3): 629-632, 638.

ZHOU Jian, PENG Su-quan, FAN Ling. Particle flow simulation of active earth pressure distribution on rigid retaining wall[J].Rock and Soil Mechanics, 2008, 29(3): 629-632, 638.

[16] 彭述权. 砂土挡墙破坏机理宏细观研究[D]. 上海: 同济大学土木工程学院, 2007: 30-100.

PENG Shu-quan. Macro-scale and meso-scale study on failure mechanism of sand retaining wall[D]. Shanghai: Tongji University. School of Civil Engineering, 2007: 30-100.