多目标土地利用空间优化配置模型及其应用
2011-06-01张鸿辉曾永年刘慧敏
张鸿辉 ,曾永年,刘慧敏
(1. 中南大学 地球科学与信息工程学院,中南大学空间信息技术与可持续发展研究中心,湖南 长沙,410083;2.长沙市规划信息服务中心,湖南 长沙,410013)
由于土地利用空间优化配置目标的多样性,如最大可能节约土地资源、最小化环境不兼容性等,土地利用空间优化配置是一种多目标决策问题[1],如何找到一种客观、量化且能解决多目标决策问题的空间优化配置方法对土地利用空间优化配置研究至关重要。作为一种通用的全局优化算法,遗传算法(Genetic algorithms, 简称GA)已被许多研究人员用于定量求解多目标土地利用空间优化配置问题[2-5]。虽然这些研究表明遗传算法是一种定量求解多目标土地利用空间配置问题的有效方法,但是,在实际应用中,当优化问题比较复杂时,遗传算法容易陷入局部最优解,并且随着问题复杂程度的增加,陷入局部解的可能性和收敛时间也随之增加[6];同时,其无法考虑影响土地利用空间优化配置的各类智能体之间的相互作用关系,因此,仅使用以遗传算法为代表的进化算法来解决复杂的土地利用空间优化配置问题还远远不够,必须更加深层次地挖掘智能计算方法来解决此类问题。基于复杂适应系统理论的多智能体系统(Multi-agent system,简称MAS)在帮助计算机实现智能计算方面已获得显著成果[7],已有不少研究者采用该方法解决土地利用空间优化配置问题[8-10]。研究表明:由于考虑了智能体对土地利用变化的影响及土地利用配置过程中智能体之间的互动关系,多智能体系统不失为一种有效解决土地利用空间优化配置问题的智能计算方法,并且多智能体系统的网格结构使得其在每个智能体的局部邻域进行择优操作,而不是作用于整个群体,因而可以保证群体的多样性,使得模型不易陷入局部最优解[11],这一点正是运用遗传算法求解多目标优化问题所特别需要的;因此,相比单一使用遗传算法方法求解多目标土地利用空间优化配置问题,结合多智能体系统与遗传算法的方法将会获得更优的解决方案,而目前这方面的研究尚未见报道。为此,本文作者从模拟生物对环境的能动适应性和生物间竞争、协同关系出发,在设定的目标与约束条件下,设计应用于土地利用空间优化配置的多智能体遗传进化算法,构建面向“资源节约”与“环境友好”的多目标土地利用空间优化配置 MOSOLUA (Multi-objective spatial optimization model for land use allocation)模型,并以国家资源节约型和环境友好型社会(简称两型社会)建设综合配套改革实验区——长株潭城市群的核心区域为例进行实证应用研究。
1 基于多智能体遗传进化算法的MOSOLUA模型
模型的基本思想是基于参与土地利用利用空间优化配置的各类Agent对土地利用环境的感知和反作用的能力解决多目标土地利用空间优化配置问题。在模型中,参与土地利用空间决策的各个Agent之间存在激烈的竞争与合作,同时,每个Agent具有一定的知识,可以利用自身的知识进行启发式搜索,以提高自身的能量和对环境的适应能力。正是由于每个 Agent利用其所固有的特性和其邻域内的其他Agent相互作用,并通过交叉、突变、死亡、自学习等过程完成多智能体种群的更替,才实现了每一代的进化,进而最终解决多目标土地利用空间优化配置问题。
1.1 模型目标函数
土地利用空间优化配置不仅应做到最大程度地节约土地资源,提高土地利用效率,同时还应尽可能地提高土地利用的环境友好程度;因此,本文设定资源节约与环境友好为模型的总体目标,为加强模型的可操作性,针对这2个目标分别设定相应的子目标,并设定相应的约束条件。以下为模型的目标以及约束条件的具体描述。
资源节约型目标:

式中:j为土地利用单元位置;l和m为土地利用类型,其取值范围为{1,2,…,k};k为土地利用类型个数;u为未开发的土地;U为未开发的土地利用单元集合;D为已开发的土地利用单元的集合;Bj为土地利用单元j的邻域内未开发的单元集合;ej为单元j目前的土地利用类型;clm为土地利用类型l与m之间的环境兼容系数;sj为土地利用单元j的邻域内已被开发的单元个数;dj为单元 j距最近的已开发的土地利用单元的距离;plm为土地利用类型l变更为类型m的费用(以单元为单位);b为土地利用空间优化配置后单元j的邻域内已开发单元的最低要求个数。当未开发单元 j被配置为土地利用类型m时,xjum为1,否则为0;当目前土地利用类型为ej的单元j的用途被更改为m时,xjejm为1,否则为0;当单元j的土地利用类型发生变更时,xik为1,否则为0[12]。
目标(1)和(2)属于资源节约型目标。目标(1)是使新开发区域与已开发区域的空间距离最小化,以避免低密度、粗放型的土地利用方式,促进土地集约利用、提高土地利用效率;目标(2)是使因用地单元用途变更而产生的总费用最小化,以节约土地开发成本;目标(3)属于环境友好型目标,它是使单元j与其邻域内的其他单元之间的环境不兼容性最小化,以促进环境友好的土地利用模式的形成;约束(4)和(5)保障只有1种土地利用类型被分配给单元 j;约束(6)为用地连通性和紧凑性约束,该约束通过确保新增城市用地单元 j的邻域内已开发用地单元个数不得小于临界值 b,而迫使新增城市用地通过填充城市内部未开发土地的方式扩展,避免新增城市用地无限制地往外扩展;约束(7)使得土地利用类型 l和 m既可以占用未开发的单元,也可以占用已开发的单元。
1.2 模型算法
[13-14],在结合多智能体系统与遗传算法各自优点的多智能体遗传算法的基础上,设计了应用于土地利用空间优化配置的多智能体遗传进化算法。该算法将遗传算法中的每一个体当作有协作能力的 Agent,每个 Agent都具有一定的能量和行为,所有 Agent都分布在上文所描述的规模为的二维土地利用空间网格上,每个Agent占据1个格点位置。它通过与邻域中Agent之间的竞争、合作以及自学习来提高自身的适应能力,被Agent占据的土地利用网格将随分布于其上的Agent类型的改变而变更其土地利用状态。
1.2.1 智能体结构
本研究中的智能体(Agent)理解为可以感知和反作用于土地利用环境的实体。在土地利用空间优化配置多智能体遗传进化算法中,Agent结构对算法的功能影响很大,各种Agent的复杂性、适应性、智能都要通过Agent的结构、规则、行为、智能度来体现。根据Agent进行土地利用空间决策的特点,用一个四元属性组描述Agent的结构,具体定义如下:
Agent=<类型,决策变量,决策参数,适应度> (8)式中:类型指参与土地利用空间决策的各类 Agent,如居民、企业主等;决策变量与决策参数分别代表Agent进行土地利用空间决策过程中所选择的决策因素以及各因素对应的权重;适应度反映Agent在土地利用空间决策过程中的适应能力,其值决定Agent在决策过程中的竞争力。
1.2.2 智能体进化算子
设计邻域竞争算子、邻域交叉算子、变异算子、智能体自学习算子共4种智能体进化算子实现智能体之间的竞争、合作、自学习等相互作用行为,模拟智能体的进化过程,从而实现土地利用空间优化配置。在此过程中,Agent主要通过影响与其存在互动关系的Agent的土地利用空间决策参数,从而影响其适应度。为计算方便,用式(9)表示Agent结构的主要属性,并以该形式将其输入智能体进化算子参与计算,其他诸如类型、决策变量、适应度等属性则以附加属性的形式输入算子,不参与具体计算,但适应度将随决策参数的变化而变化。
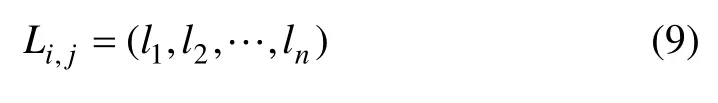
式中:Li,j为分布于土地利用网格(i,j)处的 Agent;li(i=1,2,…,n)代表Agent所选择的决策变量对应的决策参数;n为决策变量的个数。由于不同类型的Agent决策变量的量纲不一致,在输入算子前,需采用隶属函数对其进行标准化处理,本文采用级差标准化法(式(10))将标准化数据压缩到闭区间[0,1]。

(1) 邻域竞争算子。该算子利用邻域信息实现Agent之间的竞争。设算子作用智能体Li,j=(l1,l2,…,ln)上, maxi,j=(m1, m2,…,mn)为 Li,j邻域内适应度最大的智能体(其中,li和mi(i=1,2,…,n)均为智能体决策参数),若 Li,j比 maxi,j的适应度大,则可继续存活在网格上;否则必须死亡,空出的格点被maxi,j占据。若Li,j与maxi,j类型相同,则maxi,j按式(11)产生1个与其同类型的新智能体Newi,j=(e1,e2,…,en)放在空出的格点上;若Li,j与maxi,j类型不同,则先按式(12)将maxi,j映射到区间[0,1]上,然后,根据式(13)确定 N ewi,j'=(,…,en'),最后,根据式(14)将 N ewi,j'映射回区间上以得到 N ewi,j。

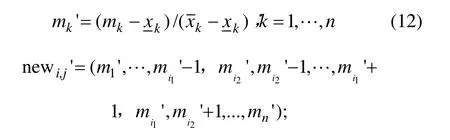
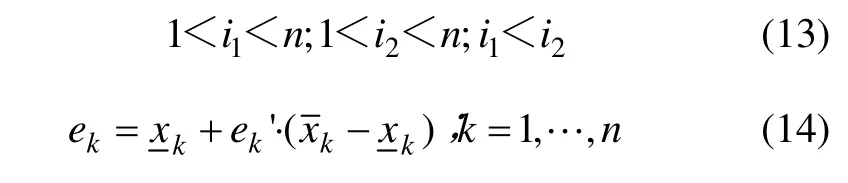
(2) 邻域交叉算子。该算子利用邻域信息来实现智能体之间的合作。本文中的邻域交叉算子采用精英保留策略,目的是使种群更快地向最优解空间进化,减少无谓的随机性退化,而由此造成的种群多样性的减少量可以通过变异算子进行补偿。该算子作用于Li,j和 Li,j邻域内与 Li,j类型相同、适应度最大的智能体maxi,j上,交叉时采用顺序交叉算子,通过该算子的作用产生2个新的智能体,保留适应度大的智能体;重复上述过程m次(m<5),从中选出适应度最大的智能体max。如果max的适应度比Li,j的大,则用它替代Li,j,否则不进行替代[14]。
(3) 变异算子。受某些突发因素影响,智能体在土地利用决策过程中的决策参数可能会发生突变。采用变异算子来描述这种突发情形。Li,j=(b1,b2,…,bn)为 Li,j=(l1,l2,…,ln)变异后的表现形式。bi(i=1,2,…,n)根据下式确定:

式中:k=1,…,n;G(0,1/t)为Gauss分布的随机数;t为进化代数。
(4) 智能体自学习算子。智能体自学习算子可以看成是一个小规模的多智能体遗传进化算法,它作用于每一代中适应度最大的智能体上,通过学习进一步提高其适应度。为了提高自学习过程的收敛速度,将邻域交叉算子也加入自学习算子中,并在算子中设置较大的交叉概率(Pc≥0.8)和较小的变异概率(Pc≤0.1)。智能体自学习时搜索半径应小于 N(其中,N为网格个数,为 5~10)。对于每一代中适应度最大的智能体,首先以其为中心,根据搜索半径产生N×N的智能体网格,然后在该网格内,对智能体分别执行邻域竞争、邻域交叉、变异算子,经过一定次数进化后,从网格中选择1个适应度最高的智能体作为学习后的智能体。
1.2.3 智能体适应度计算方法
在土地利用空间优化配置多智能体遗传进化算法中,通过比较适应度来衡量智能体的优劣,而智能体优劣可以用适应度表征。适应度通过由目标函数变换而成的适应度函数(Fitness function)求取。本文采用排序方法将种群中所有智能体对不同目标函数的优劣进行排序,从而计算总适应度。
用 Z(i)(i=1,2,…,n)表示目标函数(n为目标个数)。对于每一个目标i,智能体Xj(j=1,2,…,N,N为智能体总数)会依据对该目标的函数值Hi(Xj)优劣生成一个可行解的排序序列Y。对每一个目标都排序后,可以得到该智能体对全部目标函数的总体表现。根据智能体的排序计算其适应度:

式中:i=1,2,…,n;j=1,2,…,N;N为智能体总数;Xj为种群的第j个智能体;Yi为其在种群所有智能体中对目标 i的优劣排序后所得的序号;Fi(Xj)表示Xj对目标i所得的适应度;fit(Xj)为Xj对全部目标所得的综合适应度函数;k为区间(1,2)中的常数,用于加大个体的函数值表现最优时的适应度。由式(16)和(17)可以看出:对于总体表现较优的智能体能得到更大的适应度,获得更多的参与进化的机会[15]。
为尽可能保持种群的多样性,避免遗传漂移现象,从而达到同时探索多个区域的目的,引入基于共享机制的小生境技术以减少相似个体的复制量。按下式估算小生境半径(σshare)[16]:

式中:Fits(Xj)为经共享后的Xj对全部目标所得的综合适应度函数;Xk为种群的第 k个智能体;s(Xj,Xk)为智能体共享系数。

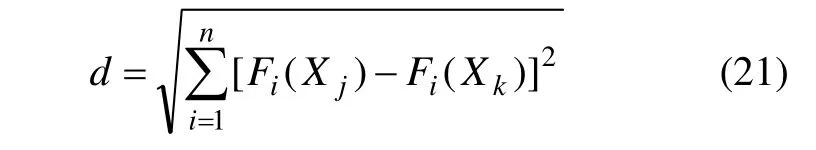
在土地利用空间优化配置过程中,智能体所处土地利用网格对智能体所期望的土地利用目标的适宜性对智能体的适应度也具有一定的影响。考虑此类影响后的智能体适应度函数如下式所示:
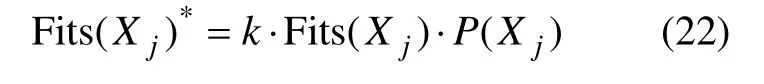
式中:k为调节参数;P(Xj)为智能体Xj对其所处土地利用网格的决策满意度,
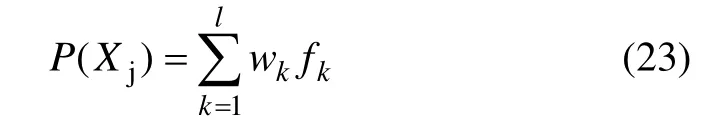
l为决策变量的个数;wk为决策参数;fk为决策变量。
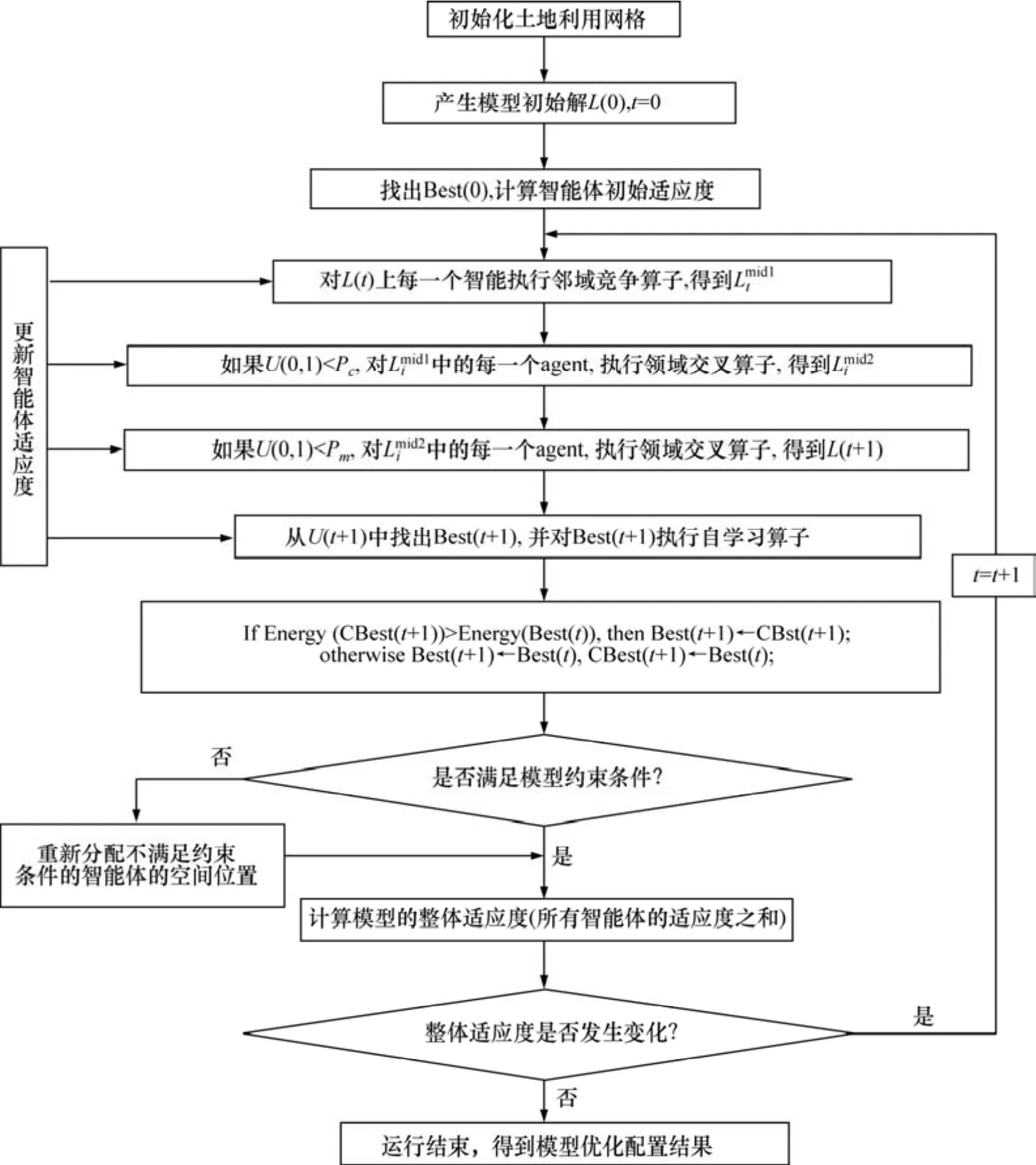
图1 MOSOLUA模型流程图Fig.1 Flow chart of MOSOLUA model
1.3 模型流程
MOSOLUA的具体流程如图1所示。图1中:L(0)为模型的初始解;L(t)为模型运行到第t代时所产生的解;和为模型运行的中间解;Best(0)和Best(t)分别表示 L(0)与 L(0),L(1),…,L(t)中适应度最大的智能体;CBest(t)表示 L(t)中适应度最大的智能体;Pc为邻域交叉概率;Pm为变异概率;U(0,1)为均匀分布的随机数。
首先初始化土地利用网格,得到模型初始解,进而计算各个Agent的适应度,并执行智能体进化算子,随后判断经过进化后的Agent集合是否满足模型的约束条件。若不满足,则通过局部空间搜索,调整不满足约束条件的Agent的空间位置,使其满足模型的约束条件;若经过进化后的Agent集合满足模型的约束条件,则计算该集合中所有Agent的适应度之和,得到模型的整体适应度,然后,通过不断地运行模型,直到满足下面的规则时,模型终止运行。
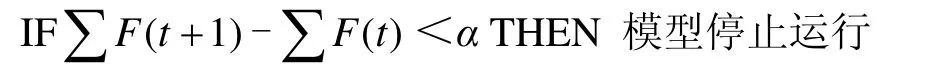
式中:∑ F (t + 1 ),∑F(t)为模型在t+1和t时刻的整体适应度;α是1个很小的值。最后,以运行过程中所得到的具有最大整体适应度的Agent集合作为模型的最优解输出,该最优解对应的土地利用网格即为满足模型要求的空间优化配置结果。
(1)把握度量单位的数学功能和本质特征.没有度量就没有数学,度量是人们认识数学,进而认识现实世界的基本工具和表达语言,是可以因人而异的.度量单位的确立是为了人们能够对度量进行统一的表达和无歧义的交流,因此度量单位必须能够揭示度量的本质,能够得到人们的共识.度量的本质在于表现事物某些指标的顺序,比如:数量的多少以及抽象出来的数的大小;距离的远近;重量的轻重;速度的快慢.
2 模型应用
2.1 实验区与数据
本文选择长株潭城市群两型社会实验区的核心区域——长沙市作为实证研究区域。研究所采用的数据包括遥感数据、GIS数据、社会经济统计数据、环境统计数据等。遥感数据包括 2005年长沙市 TM 和QuickBird数据,主要用于提取未开发用地、山体、水体、绿地等信息;GIS数据包括:比例尺为1:5万的2005年长沙市土地利用现状数据,长沙市土地利用总体规划(1997—2010年),长沙市城市总体规划(2003—2020年),长沙市商业网点规划,比例尺为1:1万的长沙市电子地图(包括学校、医院、银行、居民点、商业、工业等多种专题信息),长沙市交通分布图,长沙市基准地价图,长沙市数字高程模型(分辨率为30 m)等。其中:数字高程模型为ArcGIS软件的GRID格式,其他矢量数据为ArcGIS软件的Shapefile格式。社会经济统计数据包括从长沙市统计局及长沙市统计年鉴获取的1993—2006年长沙市人口统计、城镇居民收入等数据;环境统计数据包括从长沙市环境保护局获取的2000—2005年长沙市环境质量报告等数据。
2.2 长沙市多目标土地利用空间优化配置
2.2.1 初始化土地利用网格
由于本文主要的研究对象为城市土地利用的空间优化配置,故土地利用分类的重点为城市土地,依据城市土地功能的重要性,将研究区内已开发的土地归类为居住用地、商业用地、工业用地3种类型;此外,为简化土地利用分类的复杂性,提高程序运行速度,将尚未开发的土地归类为未开发用地、不可建设用地(主要为山体、水体、绿地、城市规划保护用地等)2种类型。因此,通过对已有的土地利用数据进行整理、归并,将研究区域的土地利用分为居住用地、商业用地、工业用地、未开发用地、不可建设用地等5种类型,土地利用网格划分为30 m×30 m。
2.2.2 初始可行解的产生
在本研究中,模型采用3×3的邻域结构,邻域内已开发用地单元个数临界值b取为3。根据模型设定,每一个土地利用网格上只能分配1种土地利用类型,也只能容纳1个Agent,根据研究区域1993—2005年人口现状,采用灰色GM(1,1)预测模型得到研究区域2010年的居住用地、商业用地、工业用地需求数量分别为69.42,45.85和30.39 km2,根据该需求数量按比例确定2010年居民Agent、工业企业Agent、商业企业Agent的数量。这里,1个Agent只是反映了比例关系,并不是只代表1个人或1个企业,在本文中的实际含义为30 m×30 m的1个网格平均容纳的人口数量或企业数量。接下来将这些Agent根据类型对应分配至 2005年土地利用网格上,剩余的待分配的Agent运用Montocarlo方法分配给研究区域内的未开发土地利用网格,这些网格的土地利用类型随分布于其上的Agent类型的变化而发生变更。这一步产生模型的父代个体即模型的初始解。
2.2.3 智能体结构与决策参数确定
在本文中,主要定义3种智能体类型,分别为居民Agent、商业企业Agent和工业企业Agent。同时,为体现同类型智能体决策时的内部异质性与差异性,根据收入,将居民Agent分为高收入(年收入>5万元)、中等收入(1.2万元<年收入<5万元)和低收入(年收入<1.2万元)3个子类型;根据企业的环保程度,将工业企业Agent分为污染型、环保型2个子类型;根据企业的规模,将商业企业Agent分为大商场型与零售型。不同收入阶层的居民Agent的比例从长沙市统计局获取,工业企业和商业企业的子类型比例主要通过对典型地区进行抽样调查获取。居民收入、企业的环保水平等数据将作为Agent的属性输入模型中。
不同类型的Agent具有不同的决策变量与决策参数。在本文中,居民Agent的主要决策行为是选择合适的区位作为居住地,而企业Agent的主要决策行为则是选择合适的区位作为企业发展用地[17]。经咨询相关行业专家,给出坡度、土地价值、环境价值、规划完备度、交通通达度、产业聚集度等决策变量供Agent选择,不同类型的Agent选择的决策变量不同,并且其决策参数也不同。各种类型Agent所选取的决策变量及其决策参数结果如表1所示,决策参数采用AHP法求得。
依据表1和式(23)可计算智能体Xj对其所处土地利用网格的决策满意度P(Xj)。适应度的计算参照本文1.2.3节中所描述的方法,首先依据Agent对目标函数值的优劣得到各智能体对各个目标的排序序列,然后,依据式(16)计算各 Agent对各个目标的适应度,依据式(17)计算各 Agent对所有目标的综合适应度,再依据式(18)~(21)得到各Agent经共享后对所有目标的综合适应度;最后,依据依据式(23)计算 Agent的决策满意度,并将其代入式(22),得到 Agent的最终适应度。在上述计算过程中,Agent对目标(1)的函数值通过计算Agent所在土地利用网格与最近的已开发的土地利用网格的距离得到,Agent对目标(2)的函数值通过计算土地用途转换的开发费用得到,土地用途转换的开发费用标准见表 2;Agent对目标(3)的函数值通过计算该Agent的3×3邻域内其他Agent所期望的土地利用目标与该Agent所期望的土地利用目标之间的兼容性之和得到。不同土地利用类型之间的环境兼容性见表3[12]。
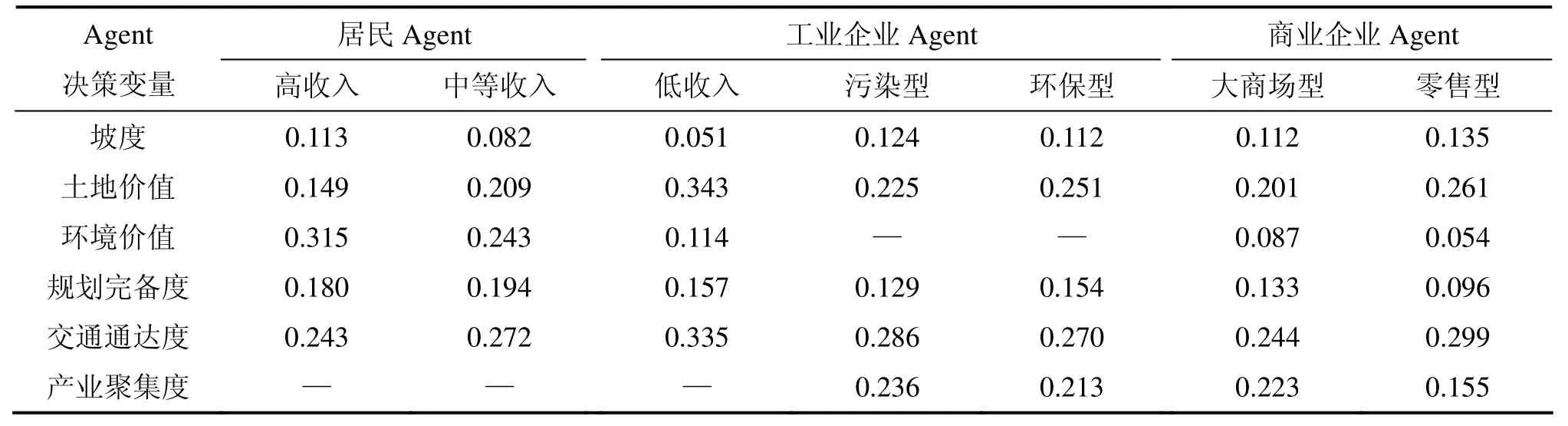
表1 Agent决策变量及决策参数Table1 Agent’s decision-making variables and decision-making parameters
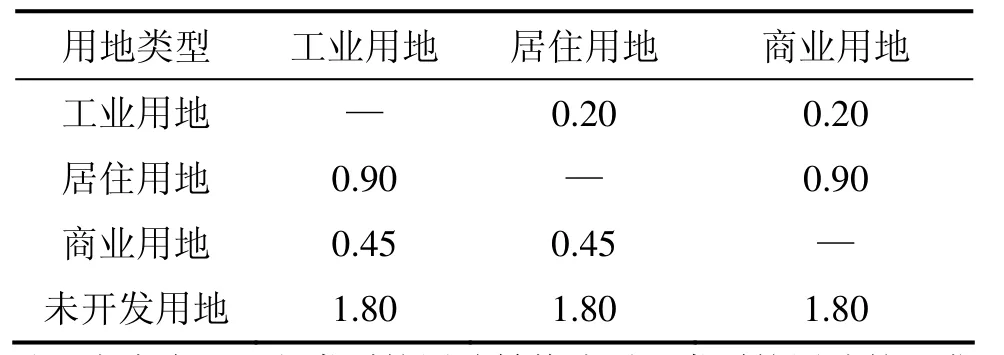
表2 土地用途转换的开发费用标准Table2 Standard of land development cost of land use type conversion 万元/土地利用网格
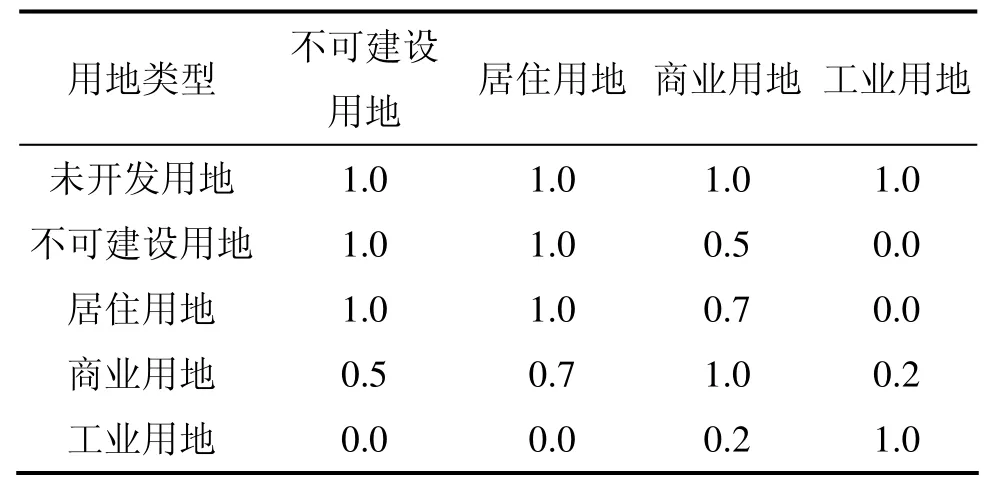
表3 相邻土地利用类型之间的环境兼容性Table3 Environmental compatibility of adjacent land uses
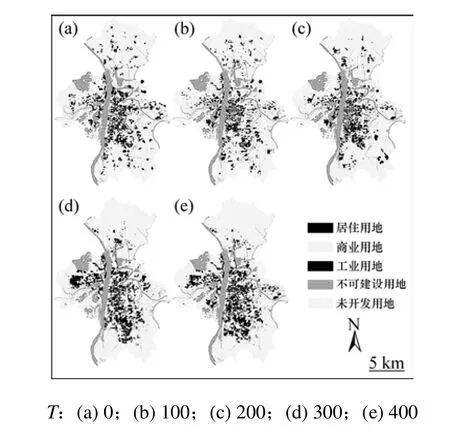
图2 MOSOLUA模型的土地利用空间优化配置过程Fig.2 Land use allocation processes using multi-objective spatial optimization allocation model
2.2.4 多智能体进化
根据1.2.2节中设计的多智能体进化算子,对分布于土地利用网格上的多智能体执行进化操作,具体包括如下几步:
(1) 对土地利用网格上每个智能体执行邻域竞争算子;
(2) 对执行邻域竞争算子后的土地,利用网格上的每个智能体,若 U(0,1)<Pc,则执行邻域交叉算子(其中,Pc为交叉概率,在本研究中,Pc=0.85);
(3) 对执行邻域交叉算子后的土地,利用网格上的每个智能体,若U(0,1)<Pm,则执行变异算子(其中,Pm为变异概率,在本研究中,Pm=0.05);
(4) 从当代所有智能体中找出适应度最大的Agent,对该Agent执行自学习算子;
(5) 若停止准则满足,则输出具有最大总体适应度的智能体集合,模型运行结束;否则令t=t+1,并转步骤(1)。
2.2.5 长沙市土地利用空间优化配置结果
在确定了智能体结构与决策参数后,按照模型的实现流程,采用多智能体遗传进化算法对长沙市土地利用进行空间优化配置。图2所示为对应于模型不同运行时间点的土地利用空间优化配置过程结果。其中:T=0代表模型处于初始状态;T=400代表模型运行了400次。
3 结果分析
2010年长沙市居住用地、商业用地、工业用地的空间优化配置模式如图 3(b)所示。与优化配置前的2005年长沙市上述三类用地的空间分布格局(图 3(a))对比可看出:优化后的居住用地、商业用地、工业用地整体上空间分布更加集中、紧凑,土地利用斑块内部的空地及城市近郊的零星土地利用斑块大大减少,同类型土地利用的空间集聚程度也更高,并且新增城市用地的增长方式多为内部填充,避免了城市土地的过度扩张。
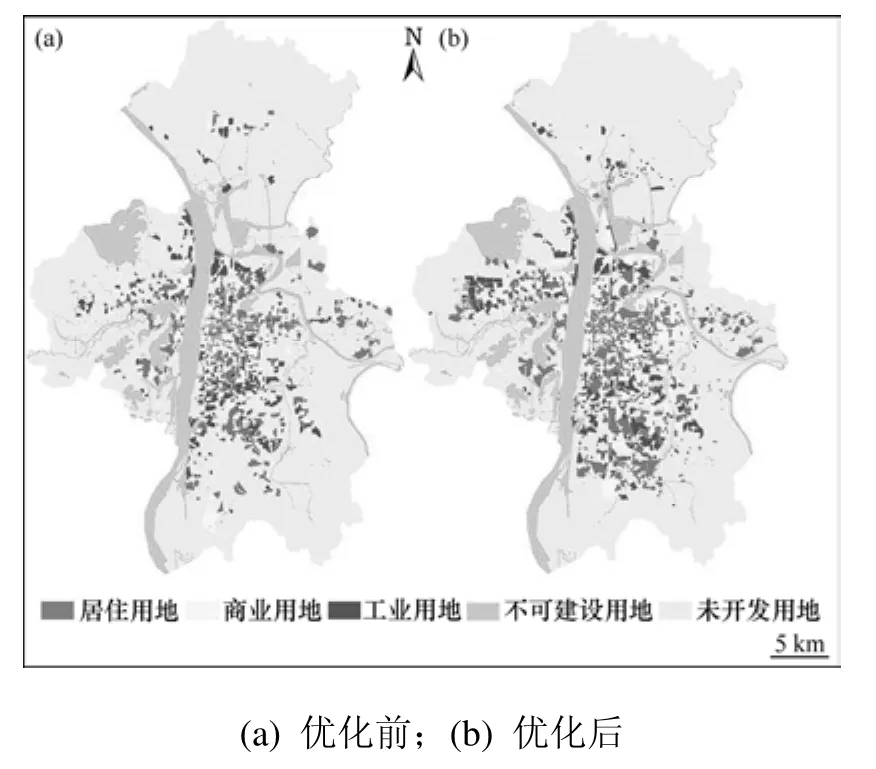
图3 优化配置前后土地利用空间格局比较Fig.3 Comparison of land use spatial patterns before and after spatial optimization
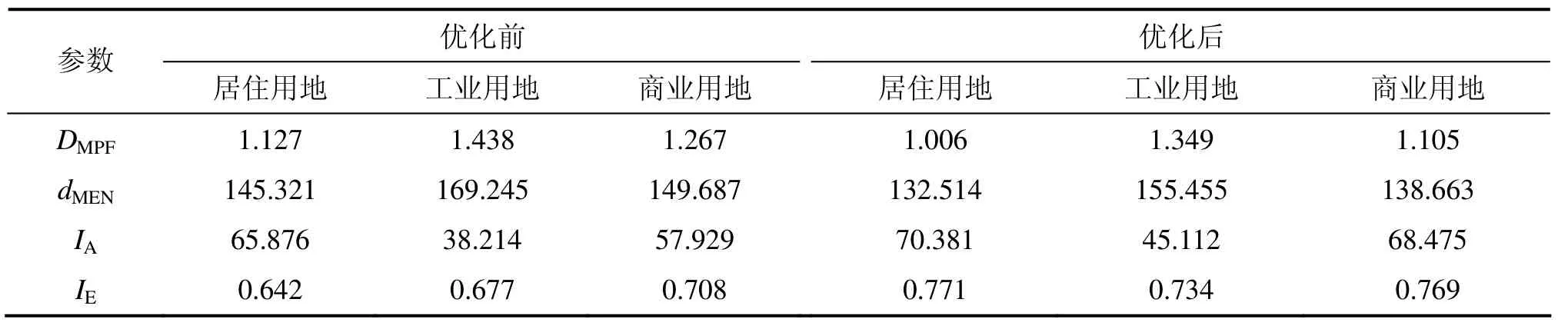
表4 优化前、后的土地利用空间格局的评价结果Table4 Evaluation on land use spatial patterns before and after spatial optimization allocation
为定量分析优化前、后的土地利用空间配置模式,结合本研究所设立的目标函数,采用平均斑块分维数(Mean patch fractal dimension,DMPF)、平均斑块最邻近距离(Mean euclidean nearest-neighbor distance,dMEN)和聚集指数(Aggregation index,IA)等空间格局指标来评价某一土地利用类型斑块总体呈紧凑型的程度,即土地资源节约程度;采用环境兼容性指数(Environmental compatibility,CE)来评价某一土地利用类型的环境友好程度。DMPF,dMEN和IA的计算公式参见文献[18]。CE的计算公式为:

其中:ei为斑块 i与其邻域内相邻土地利用单元的环境兼容性;n为斑块数目。表4所示为基于上述指数对研究区域优化前、后的居住用地、工业用地、商业用地空间格局的评价结果。从表4可看出:优化后的各类用地的DMPF和dMEN均比优化前的低,而IA和IE则比优化前的高。这说明优化后的土地利用空间格局的斑块邻接性、连接性、聚集度、紧凑度、环境兼容性均较优化前有较大提高,从而也证明优化后土地利用配置模式的总体资源节约与环境友好程度要比优化前的高。
为进一步验证模型的可行性,基于相同的目标函数,比较了采用该模型和采用普通遗传算法空间优化配置模型得到的土地利用配置结果(图 4(a)和(b))以及2种模型的收敛性能(图 5),并根据 DMPF,dMEN,IA和IE,评价了采用普通遗传算法空间优化配置模型得到的土地利用配置结果(表5)。
从图4可发现:基于MOSOLUA模型所得到的土地利用配置结果的空间格局较基于普通遗传算法空间优化配置模型获取的土地利用配置结果更为规则、紧凑,而从图5则可发现:对同一研究区域的土地利用进行空间优化配置,采用普通遗传算法空间优化配置模型与MOSOLUA模型,得到最终土地利用空间优化配置结果时的模型总体适应度分别为14.88和16.75,MOSOLUA模型的总体适应度与普通遗传算法空间优化配置模型的相比均提高了12.57%。对比表5与表4还可发现:表5中各类用地的DMPF和dMEN均比表4中优化后的高,而IA和IE则比表4中优化后的低,反映了基于 MOSOLUA模型所得到的土地利用配置结果的总体资源节约与环境友好程度明显比基于普通遗传算法空间优化配置模型获取的土地利用配置结果好。此外,对于同一研究区域,基于相同的目标函数,为得到优化配置结果,MOSOLUA模型和普通遗传算法空间优化配置模型实际运行的总时间分别为8.57 h和3.31 h,MOSOLUA模型的运行效率比普通遗传算法空间优化配置模型的运行效率提高了61.38%。

图4 MOSOLUA模型与普通遗传算法空间优化配置模型的配置结果比较Fig.4 Comparison of land use allocation results using different allocation models
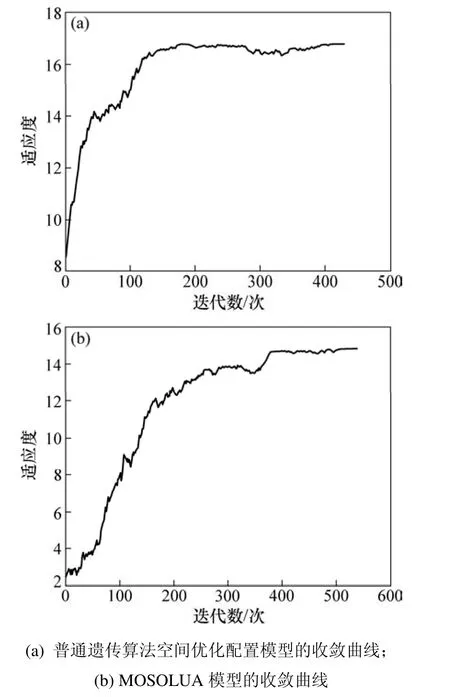
图5 MOSOLUA模型与普通遗传算法空间优化配置模型的收敛性比较Fig.5 Comparison of convergence curves using different allocation models

表5 基于普通遗传算法空间优化配置模型的土地利用配置结果评价Table5 Evaluation on land use allocation results using GA spatial optimization allocation model
4 结论
(1) “资源节约”与“环境友好”目标约束下,从模拟生物对环境的能动适应性和生物间竞争、协同关系出发,构建了多目标土地利用空间优化配置MOSOLUA模型,为土地资源的科学规划与管理问题的合理解决提供了新的有效方法。
(2) MOSOLUA模型与采用普通遗传算法的模型相比,收敛速度快,其运行效率与普通遗传算法空间优化配置模型相比提高了61.38%;采用该模型优化配置的土地利用空间格局从斑块紧凑度、邻接性、聚集度、环境兼容性、总体资源节约与环境友好程度方面均比采用普通遗传算法模型的配置结果优,并且模型的总体适应度与采用普通遗传算法的模型相比提高了12.57%。上述研究结果验证了MOSOLUA模型的合理性与先进性。该模型可为政府和城市规划工作者制定用地政策提供定量的辅助决策依据。
(3) 土地利用空间优化配置是一个复杂的多目标决策过程,尽管本研究考虑了资源节约与环境友好等目标,但是,在实际土地利用过程中,土地利用空间优化配置需考虑的目标往往更多或更复杂,如政策约束、资源约束、生态建设用地需求等;因此,在其他区域的应用中利用该模型时,应根据实际情况制定合适的目标体系。
参考文献:
[1] Duh J D, Brown D G. Knowledge-informed Pareto simulated annealing for multi-objective spatial allocation[J]. Computers,Environment and Urban Systems, 2007, 31(3): 253-281.
[2] 黎夏, 叶嘉安. 遗传算法和 GIS结合进行空间优化决策[J].地理学报, 2004, 59(5): 745-753.
LI Xia, YE Jia-an. Optimal spatial search using genetic algorithms and GIS[J]. Acta Geographica Sinica, 2004, 59(5):745-753.
[3] 姜友华, 王新生. 遗传算法用于产生可供选择的城市规划方案[J]. 武汉大学学报: 工学版, 2002, 35(3): 63-66.
JIANG You-hua, WANG Xin-sheng. Using genetic algorithms to generate alternative schemes for urban planning[J]. Engineering Journal of Wuhan University, 2002, 35(3): 63-66.
[4] Holzkamper A, Seppelt R. A generic tool for optimising land-use patterns and landscape structures[J]. Environmental Modelling &Software, 2007, 22(12): 1801-1804.
[5] Stewart T J, Janssen R, van Herwijnen M. A genetic algorithm approach to multi objective land use planning[J]. Computers &Operations Research, 2004, 31(14): 2293-2313.
[6] 杜国明, 陈晓翔, 黎夏. 基于微粒群优化算法的空间优化决策[J]. 地理学报, 2006, 61(12): 1290-1297.
DU Guo-ming, CHEN Xiao-xiang, LI Xia. Spatial optimal search based on particle swarm optimization[J]. Acta Geographica Sinica, 2006, 61(12): 1290-1297.
[7] LIU Ji-ming, TANG Yuan-yan, Cao Y C. An evolutionary autonomous agents approach to image feature extraction[J].IEEE Trans on Evolutionary Computation, 1997, 1(2): 681-688.
[8] Saarloos D J M, Arentze T A, Borgers A W J, et al. A multi-agent paradigm as structuring principle for planning support systems[J].Computer, Environment and Urban Systems, 2008, 32(1):29-40.
[9] 黎夏, 叶嘉安, 刘小平, 等. 地理模拟系统: 元胞自动机与多智能体[M]. 北京: 科学出版社, 2007: 64-66.
LI Xia, YE Jia-an, LIU Xiao-ping, et al. Geographical simulation system: Cellular automata and multi-agent system[M]. Beijing:Science Press, 2007: 64-66.
[10] 刘小平, 黎夏, 叶嘉安. 基于多智能体系统的空间决策行为及土地利用格局演变的模拟[J]. 中国科学: D辑, 2006, 36(11):1027-1036.
LIU Xiao-ping, LI Xia, YE Jia-an. Multi-agent systems for simulating spatial decision behaviors and land use dynamics[J].Science in China: Series D, 2006, 36(11): 1027-1036.
[11] Cardon A, Galinho T, Vacher J P. Genetic algorithms using multi-objectives in a multi- agent system[J]. Robotics and Autonomous Systems, 2000, 33(2): 179-190.
[12] Ligmann-Zielinska A, Church R, Jankowski P. Spatial optimization as a generative technique for sustainable multi objective land-use allocation[J]. International Journal of Geographical Information Science, 2008, 22(6): 601-622.
[13] 张鸿辉, 曾永年, 金晓斌, 等. 多智能体城市土地扩张模型及其应用[J]. 地理学报, 2008, 63(8): 869-881.
ZHANG Hong-hui, ZENG Yong-nian, JIN Xiao-bin, et al. Urban land expansion model based on multi-agent system and application[J]. Acta Geographica Sinica, 2008, 63(8): 869-881.
[14] 钟伟才, 刘静, 焦李成. 多智能体遗传算法用于线性系统逼近[J]. 自动化学报, 2004, 30(6): 933-938.
ZHONG Wei-cai, LIU Jing, JIAO Li-cheng. Optimal approximation of linear systems by multi-agent genetical algorithm[J]. Acta Automatic Sinica, 2004, 30(6): 933-938.
[15] 陈南祥, 李跃鹏, 徐晨光. 基于多目标遗传算法的水资源优化配置[J]. 水利学报, 2006, 37(3): 308-313.
CHEN Nan-xiang, LI Yue-peng, XU Chen-guang. Optimal deployment of water resources based on multi- objective genetic algorithm[J]. Journal of Hydraulic Engineering, 2006, 37(3):308-313.
[16] 赖红松, 董品杰, 祝国瑞. 求解多目标规划问题的Pareto多目标遗传算法[J]. 系统工程, 2003, 21(5): 24-28.
LAI Hong-song, DONG Pin-jie, ZHU Guo-rui. A Pareto multi-objective genetic algorithm for multi-objective programming problem[J]. Systems Engineering, 2003, 21(5):24-28.
[17] 薛领, 杨开忠. 城市演化的多主体(multi-Agent)模型研究[J].系统工程理论与实践, 2003, 23(12): 1-9.
XUE Ling, YANG Kai-zhong. Researh on urban evolution using Ageng-based simulation[J]. Systems Engineering-Theory &Practice, 2003, 23(12): 1-9.
[18] 黎夏, 杨青生, 刘小平. 基于CA的城市演变的知识挖掘及规划情景模拟[J]. 中国科学: D辑, 2007, 37(9): 1242-1251.
LI Xia, YANG Qing-sheng, LIU Xiao-ping. Data mining and scenarios simulation in urban simulation based on cellular automata[J]. Science in China : Series D, 2007, 37(9):1242-1251.
