基于混合QPSO的LS-SVM参数优化及其应用

朱红求，阳春华，王 觉，桂卫华

(中南大学 信息科学与工程学院，湖南 长沙，410083)

支持向量机(SVM)[1]作为一种基于结构风险最小化学习训练方法，较好地解决了小样本、高维数、非线性、局部极小值等实际问题，具有很强的泛化能力。在此基础上，Suykens等[2]提出了最小二乘支持向量机(LS-SVM)方法，它将SVM的求解从二次规划问题转化为线性方程组，降低了 SVM 的计算复杂度，同时解决了大样本训练过程中计算速度变慢的问题，在故障检测与诊断、过程预测、文本分类、生物信息学、模式识别和冶金过程等领域获得了广泛的应用[3-8]。LS-SVM具有优良的学习能力和推广能力，然而，其参数优化选择对LS-SVM回归模型学习精度和泛化能力起着决定性作用。针对参数选取问题，国内外一些学者从不同的角度对此进行了深入的研究和探讨。传统网格搜索法的计算量大，搜索时间长，特别是在预测精度要求高和大样本的情况下尤为突出。吴景龙等[9-10]提出了基于遗传算法(GA)的支持向量机参数选择法，取得了较好的效果。考虑到粒子群算法原理简单和容易实现的优点，Huang等[11]提出了将PSO算法应用到支持向量机参数选择中，Zhou等[12]提出基于量子粒子群算法(QPSO)算法的支持向量机参数选择法。在此，本文作者采用QPSO算法对LS-SVM的参数进行优化选择，同时，为了加快搜索速度和解的精确性，引入Powell算法对QPSO算法进行改进。采用测试函数对所提出的HQPSO LS-SVM建模方法进行验证分析，并将该建模方法应用于湿法炼锌净化过程离子浓度预测。

1 最小二乘支持向量机

对于训练集(xi，yi)(xi∈Rn，yi∈R，i=1，…，l)，其中l为训练样本个数，选择一个非线性映射()φ·将n维输入，1维输出样本向量，从原空间映射到高维特征空间，则LS-SVM回归问题可表达为：

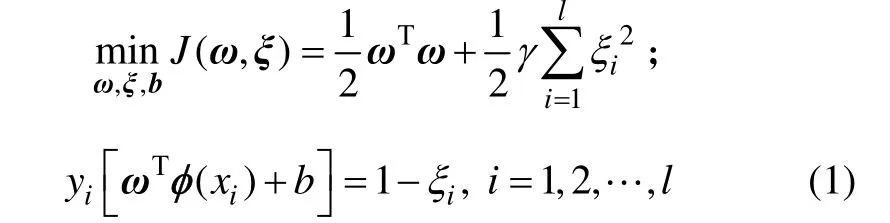
其中：ξi为松弛变量；φ (·)为映射函数；b为偏移量；w 为支持向量；ξ=(ε1，ε2，…，εl)；γ为用于平衡拟合误差和模型复杂度的正则化参数。一般地，由于ω可能为无限维，直接求解式(1)的优化问题极其困难，因此，将这一优化问题转化到其对偶空间中，引入拉格朗日函数对其进行求解，可得：

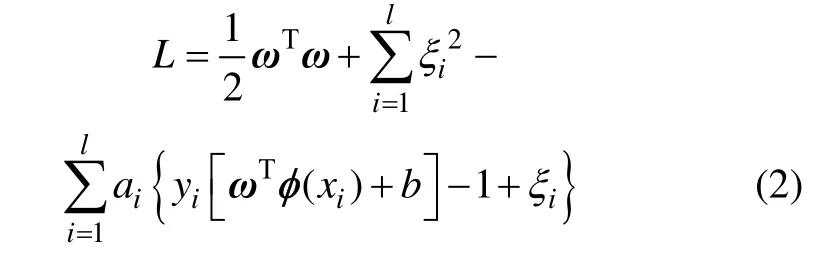
式中：ai(i=1，2，3，…，l)为拉格朗日乘子，再根据Karush-Kuhn-Tucher(KKT)最优化条件，可得线性方程组：

式中：Y=[y1，…，yl]T；ηl=[1，…，1]；a=[a1，…，al]；s=[1，…，1]T；I为单位矩阵；是满足Mercer条件的对称函数(核函数)。

应用最小二乘法求出a和b，得到LS-SVM函数回归结果为：

RBF核函数又称径向核函数或高斯核函数，是具有全局收敛特性的线性学习算法前馈网络，其学习速快，是应用最广泛的核函数，即：

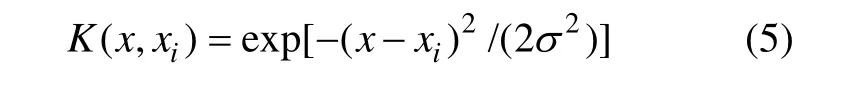
其中：σ为核宽度。

核宽度σ和正则化参数γ是LS-SVM回归模型的2个重要参数，它们的选取直接影响着算法的学习能力和泛化性能。为此，本文作者提出一种结合 QPSO算法和 Powell 算法的 HQPSO优化算法，优化选择LS-SVM回归模型中的2个重要参数，以提高模型的泛化性能。

2 基于HQPSO的LS-SVM方法

2.1 QPSO算法和Powell算法

Sun等[13]从量子力学的角度，通过对粒子收敛行为的研究，提出了量子粒子群优化算法。在QPSO中，由于粒子满足聚集态的性质完全不同，使粒子能在整个可行解空间中搜索全局最优解，因而QPSO算法在搜索能力上远比标准粒子群算法的优。QPSO 中粒子的更新方式如下：

其中：mbest为所有个体当前最佳位置的中心点；Pij为第i个个体在第j维上的最佳位置；Pgj为粒子群在第j维上的最佳位置；ijcP 为介于Pij与Pgj之间的随机位置；M为粒子群规模；φ和u为(0，1)之间的随机数；α为收缩扩张系数，它是QPSO收敛的1个重要参数，第t次迭代时可取：

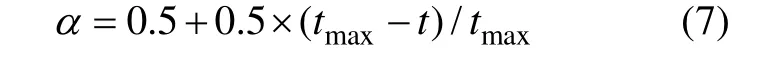
tmax为最大迭代次数。

Powell算法是以共轭方向为基础收敛速度快的直接搜索法。对于n维极值问题，首先沿着n个坐标方向求极小，经过n次之后得到n个共轭方向，然后，沿n个共轭方向求极小，经过多次迭代后便可求得最小值。对于给定的目标函数，通过任意选定的初始点出发，利用共轭方向的概念和性质逐次构造共轭方向，并以此作为搜索方向而形成的一种算法。该算法具有较快的收敛速度，但容易陷入局部最优。

在QPSO算法中引入Powell算法对其进行局部寻优，主要体现在以下3个部分：首先，在量子粒子群初始化时，对每个粒子的初始随机位置进行Powell寻优；其次，在迭代过程中对QPSO的局部最优解进行Powell寻优；最后，在QPSO搜索到全局最优解后，对其进行Powell寻优，以加快QPSO的搜索效率和提高解的精确性。

2.2 HQPSO算法的实现

Powell算法搜索方法思路简单，使用方便，具有很好的局部收敛效果，故在QPSO算法全局收敛的基础上，提出在 QPSO算法搜索过程中，使用 Powell搜索方法来提高 QPSO算法的寻优能力和解的精确性。其步骤如下：

Step 1：初始化，迭代次数t=0，限制范围内随机初始化粒子的初始速度和位置；

Step 2：对粒子的初始位置进行Powell局部寻优，得到更优的初始位置；

Step 3：计算粒子的目标函数值；

Step 4：更新每个粒子的新局部最优位置Pij；

Step 5：对每个粒子的新局部最优位置进行Powell局部寻优，得到更好的新局部最优位置；

Step 6：更新全局最优位置Pgj；

Step 7：根据式(6)计算mbest，ijcP ，并更新粒子的新位置；

Step 8：令t=t+1，重复执行Step 3 ~Step 7，直到满足迭代次数要求或精度要求；

Step 9：对Pgj进行Powell局部寻优，若最优值在若干次内保持不变，则结束寻优操作。

在量子粒子群算法的寻优过程中，对粒子随机初始位置、粒子的新局部最优位置以及全局最优解，应用Powell算法对其进行局部寻优，较大地提高QPSO算法的寻优能力和解的精确性。

3 仿真实验

为了验证上述算法的有效性，利用加有噪声的二维函数 f(x1，x2)进行仿真测试：f(x1，x2)= sin x1cos x2+σ0，x1，x2∈[-π，π]。其中：σ0是均值为 0、偏差为 0.01，0.05，0.10，0.15的高斯噪声。对噪声的每一个方差按x在区域内均匀分布，取200对数据作为一个数据集，将每个数据集中的数据分为2组：一组用作LS-SVM模型的训练，另一组用作LS-SVM模型的测试。

分别采用HQPSO算法和PSO算法对LS-SVM进行参数优化，以均方差(MSE)和平均绝对误差(MAD)作为两种算法的比较指标。设定HQPSO算法和PSO算法的迭代次数M=100，初始化群体个体数目N=30，LS-SVM 模型的初始化参数(σ，γ)范围为：σ=[0，10]，γ=[0，1 000]，以避免盲目搜索。

表1 LS-SVM参数优化平均结果比较Table1 Average results in parameters selection of LS-SVM

表 1所示为 PSO算法和 HQPSO算法分别对LS-SVM模型参数多次优化平均结果对比。从表1可见：在不同噪声干扰下，相比于PSO LS-SVM模型,HQPSO LS-SVM模型的 MSE和 MAD较小，说明HQPSO LS-SVM模型具有更高的精度和跟踪效果，进一步提高了模型的泛化性能；2种算法的MSE和MAD都比较小，说明 LS-SVM具有较强的泛化能力。

4 在湿法炼锌净化过程中的应用

净化过程[14]是湿法炼锌生产流程中的重要工序之一，净化的目的是尽可能除去对锌电解及析出锌的质量可能造成不利影响的各种杂质离子。净化过程主要由8号、4号、5号、6号和7号5个净化槽串联而成，一段后液从8号槽进入，依次经过4号、5号、6号和7号槽，其中锌粉和锑盐由8号槽加入，如图1所示。现场操作工人主要根据4号槽钴离子质量浓度来确定锌粉和锑盐的添加量，因此，实时预测4号槽的钴离子浓度对实际生产操作具有重要的现实意义。

鉴于湿法炼锌净化除钴过程4号槽钴离子质量浓度预测的重要性，本文在深入研究净化过程机理的基础上，提出基于HQPSO的LS-SVM离子浓度预测方法。以均方差(MSE)作为模型参数优化选择的标准，最优化模型参数，使得HQPSO LS-SVM预测模型具有最小的均方差。

利用湿法炼锌净化过程连续生产的在线数据对所提出的预测模型进行验证分析。随机选取工业现场某一段时间的部分连续生产数据，经过数据预处理得到300组有效数据，其中260组作为训练样本，40组进行预测。在训练前，首先对样本数据进行归一化处理，模型参数优化时，设定HQPSO迭代次数M=100，初始化群体个体数目N=30，初始化模型参数(σ，γ)的范围：σ=[0，10]，γ=[0，1000]，以避免盲目搜索。

通过HQPSO算法对LSSVM模型参数进行优化选择，得到最优化参数值：核宽度σ=1.85，正则化参数γ=171，其仿真验证结果如图2所示。

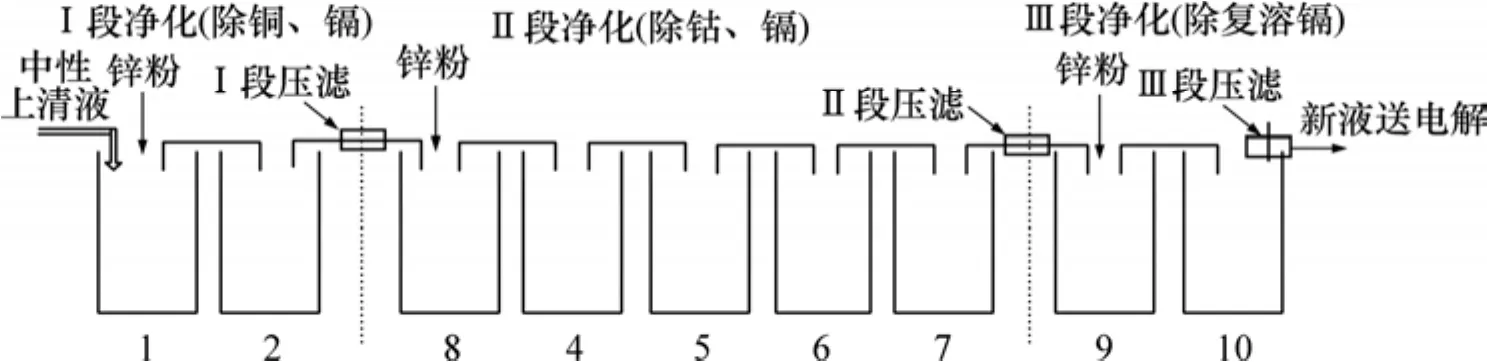
图1 硫酸锌溶液净化工艺流程Fig.1 Purification process of zinc sulfate solution

图2 4号槽Co离子浓度仿真结果Fig.2 Simulation result of cobalt concentration in No.4 tank

通过分析计算，可知均方差为0.034 8，最大相对误差为10.56%，最大绝对误差为0.544 6 mg/L，模型具有较高的预测精度。此外，净化过程工业标准为在离子质量浓度小于10 mg/L的情况下要求绝对误差小于1 mg/L。可以看出：模型预测结果满足现场工艺生产的要求，为净化过程的操作优化创造了条件。

5 结论

(1) 所提出的基于HQPSO算法的LS-SVM参数选择法，提高了LS-SVM模型的学习性能和泛化能力。

(2) 提出了结合 QPSO算法的全局优化能力和Powell的局部寻优能力的HQPSO算法。以QPSO算法为基础，在QPSO算法寻优过程中，分别对粒子的随机初始位置、新局部最优位置以及全局最优解，应用Powell算法对其进行局部寻优，以保证QPSO算法的求解速度和解的精确度。

(3) HQPSO LS-SVM模型的训练效果和预测效果好，验证了该支持向量机模型的有效性。利用湿法炼锌净化过程的实际生产数据进行仿真。基于所提出方法构造的LS-SVM 预测模型具有较好的预测精度，预测结果满足现场工艺要求，为生产过程的操作优化创造了条件。

[1] Vapnik V N. The nature of statistical learning theory[M]. New York: Springer-Verlag, 1998: 17-34.

[2] Suykens J A K, Vandewalle J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3):293-300.

[3] YUAN Sheng-fa, CHU Fu-lei. Fault diagnostics based on particle swarm optimization and support vector machines[J].Mechanical Systems and Signal Processing, 2007, 21(4):1787-1798.

[4] HONG Wei-chiang. Chaotic particle swarm optimization algorithm in a support vector regression electric load forecasting model[J]. Energy Conversion and Management, 2009, 50(1):105-117.

[5] WANG Tai-yue, CHIANG Huei-min. One-against-one fuzzy support vector machine classifier: An approach to text categorization[J]. Expert Systems with Applications, 2009, 36(6):10030-10034.

[6] Exarchos K P, Papaloukas C, Exarchos T P, et al. Prediction of cis/trans isomerization using feature selection and support vector machines[J]. Journal of Biomedical Informatics, 2009, 42(1):140-149.

[7] Wu Y C, Lee Y S, Yang J C. Robust and efficient multiclass SVM models for phrase pattern recognition[J]. Pattern Recognition, 2008, 41(9): 2874-2889.

[8] 王凌云, 桂卫华, 刘梅花, 等. 基于改进在线支持向量回归的离子浓度预测模型[J]. 控制与决策, 2009, 24(4): 537-541.

WANG Ling-yun, GUI Wei-hua, LIU Mei-hua, et al. Prediction model of ion concentration based on improved online support vector regression[J]. Control and Decision, 2009, 24(4):537-541.

[9] 吴景龙, 杨淑霞, 刘承水. 基于遗传算法优化参数的支持向量机短期负荷预测方法[J]. 中南大学学报: 自然科学版, 2009,40(1): 180-184.

WU Jing-long, YANG Shu-xia, LIU Cheng-shui. Parameter selection for support vector machines based on genetic algorithms to short-term power load forecasting[J]. Journal of Central South University: Science and Technology, 2009, 40(1):180-184.

[10] Osowski S, Siroic R, Markiewicz T, et al. Application of support vector machine and genetic algorithm for improved blood cell recognition[J]. Instrumentation and Measurement, 2009, 58(7):2159-2168.

[11] HUANG Cheng-lung, DUN Jian-fan. A distributed PSO–SVM hybrid system with feature selection and parameter optimization[J]. Applied Soft Computing, 2008, 8(4):1381-1391.

[12] ZHOU Lin-cheng, YANG Hui-zhong, LIU Chun-bo.QPSO-based hyper-parameters selection for LS-SVM regression[C]//Proceedings of Fourth International Conference on Natural Computation. Jinan: IEEE, 2008: 130-133.

[13] SUN Jun, FENG Bin, XU Wen-bo. Particle swarm optimization with particles having quantum behavior[C]// Proceedings of Congress on Evolutionary Computation. Portland: IEEE, 2004:325-331.

[14] Boyanov B S, Konareva V V, Kolev N K. Purification of zinc sulfate solutions from cobalt and nickel through activated cementation[J]. Hydrometallurgy, 2004, 73(1): 163-168.