车用柴油机振动故障混沌诊断系统及其应用

谭季秋 ，鄂加强，谭 青，邓元望，钟定清

(1. 湖南工程学院 机械工程学院，湖南 湘潭，411101；2. 湖南大学 机械与运载工程学院 湖南 长沙，410082；3. 中南大学 机电学院 湖南 长沙，410083)

车用柴油机振动是衡量柴油机工作质量的一个重要标志[1-3]。振动过大时会加速机件的疲劳破坏，降低车用柴油机的工作寿命。车用柴油机振动还会使乘员易于疲劳并有不舒适感，同时影响仪表的精度和指示，有时还使结构和仪器遭受损坏[4-6]。车用柴油机是一个内部存在不确定性因素和非线性作用机制的宏观复杂系统。在这个系统中，数据具有极复杂的非线性特征，在数学上很难用各影响因素描述[7]。车用柴油机状态监测信息能否快速而准确地被提取与及时报警，在很大程度上制约着车用柴油机的整体性能和运行能力的提高。此外，在建立振动模型时，其参数估计工作较繁琐且它们并不能直观、有效地从单变量时间序列中将系统的动力特性描绘出来。近20年来，混沌与分形理论在气象、地震、冶金、资源环境以及经济上的成功预测[8-11]为该问题的解决提供了新的思路。混沌理论能从一个输出变量的时间序列有效地提取出系统的动力特性，找出时间序列中包含的丰富信息及参与动态的全部变量的信息，达到真正认识该系统的目的。因此，如何准确地判断从车用柴油机提取的振动信号中是否含有混沌特性，已成为车用柴油机振动故障诊断中重要的基本问题。在此，本文作者采用混沌理论和计算检测技术相结合，研究被车用柴油机状态监测系统提取的车用柴油机振动信号产生机制，以便为车用柴油机振动信号的识别以及故障诊断提供一种有效且实用的新技术。

1 车用柴油机振动信号故障诊断系统设计

1.1 车用柴油机状态监测系统构成

1.1.1 硬件构成

以4105型四冲程柴油机为实验对象，分别在第1和第2缸进气阀附近的缸盖和排气阀阀壳上布置传感器，以及第1和第2缸的缸套靠近活塞上止点的位置布置传感器。测点布置与测试系统如图1所示。

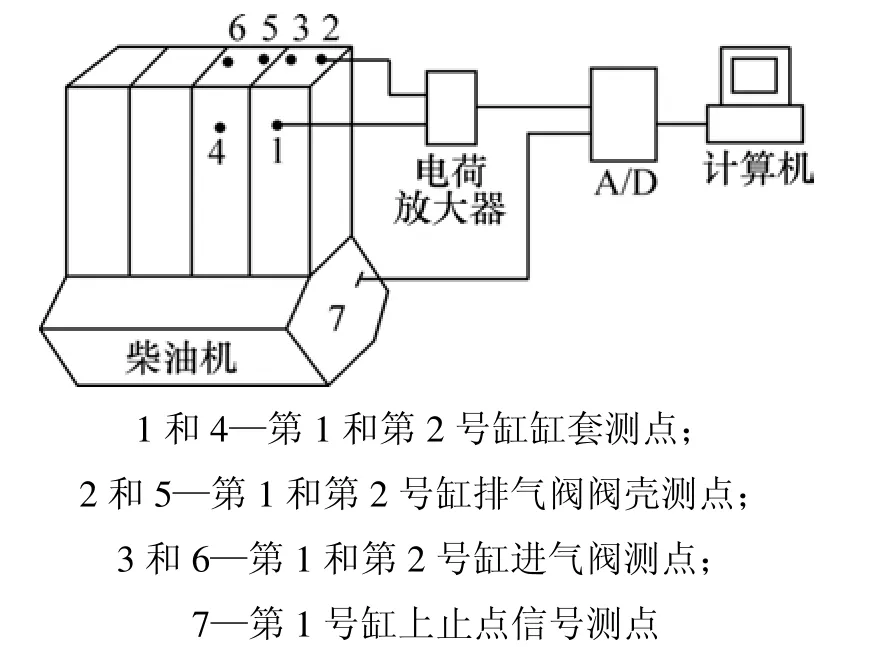
图1 测点布置与测试系统简图Fig.1 Sketch of measurement spot disposal and measurement system

振动信号用 YD系列加速度传感器测取，配用DFH型电荷放大器。

车用柴油机状况监测系统采用上、下两级结构。上位机运行于Windows NT环境下，负责从下位机调取监测数据、对数据进行处理分析以及各种报告和图表的打印等；下位机系统完成的主要功能是把测试信号转化为0~5 V或4~20 mA的标准信号，利用数据采集仪把标准信号变换为字节数据，通过RS485通信方式实时向上位机传送。

1.1.2 上位机的串行通信程序设计

从经济实用性考虑，对于车用柴油机热工状况监测系统，利用Visual C++就能实现与上位机的串行通信相关的功能。应用Visual C++开发串行通信的方法很多，常用的有：

Ⅰ. 利用Windows API通信函数；

Ⅱ. 利用Visual C++的通信控件MSComm；

Ⅲ. 利用第3方编写的C类库。

第Ⅰ种在应用程序开发中使用较广，但由于 API函数较复杂，要求了解 Windows编程的各种信息机制，对使用者有较高的要求；第Ⅱ种方法看似较简单，直接使用MSComm控件，其封装了API函数的许多功能，只需要对串行进行简单设置，但由于使用了Variant类，很容易出错，在程序调试时带来许多异常；第Ⅲ种方法是直接使用编写的通信类C类库，在Internet上有较多的第3方提供的类供选择，进行测试后可安全使用；使用C类库时只需要了解该类的成员函数，就可以正确使用。为此，在本监测系统中使用一个编写的C类库，其具体结构如下：

Class CSerial

{

public:

CSerial

CSerial

BOOL Open(int nPort=2, int nBaud=9600);

BOOL Close(void);

int ReadData(void *, int);

int SendData(const char *, int);

int ReadDataWaiting(void);

BOOL IsOpened(void)

{return(m_bOpened); }

protected:

BOOL WriteCommByte(unsigned char);

HANDLE m_hIDComDev;

OVERLAPPED

m_OverlappedRead,m_OverlappedWrite;

BOOL m_bOpened;

}

其中：CSerial( )为类构造函数，不带参数，初始化所有类成员变量；Open( )函数打开通信端口，第1个参数是串行号，第2个参数是数据传输速率，返回1个布尔值；Close( )函数关闭通信端口；SendData( )将数据从1个Buffer写到串行端口，第1个参数是缓冲区指针，其中包含要被发送的数据；ReadData( )为从端口接收缓冲区读入的数据；ReadDataWaiting( )为返回等待在通信端口Buffer中的数据，其中，第1个参数是Void*缓冲区指针，数据被送入该Buffer；第2个参数是INT类型，给出Buffer的值。

该类的使用非常方便，直接调用相关函数即可实现相关功能，且不易出错，方便程序调试和系统维护。

上位机通信程序软件设计包括：打开串行，设置通信格式，用查询方式向下位机发出命令，接收数据并实时显示报警。完成的主要操作包括：上位机向下位机发送通信开始标志“1BH”，呼叫下位机的联络地址、指令下位机接收数据等信息。车用柴油机热工状况在线监测系统通信流程如图2所示。

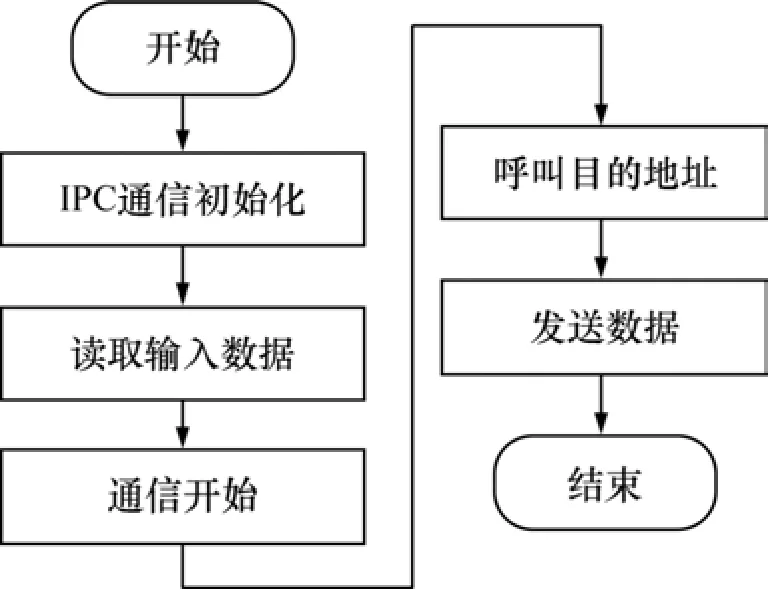
图2 监测系统通信流程图Fig.2 Communication flow chart of monitoring system

1.1.3 车用柴油机状况在线监测数据库开发

由于车用柴油机状况在线监测系统中需要保存各种实时接收的数据，并实现以后的数据再次回放，所以，需要建立数据文件。本系统将串行编程与ODBC技术相结合，将测试数据放在Access数据源文件中，通过编程接口对其进行访问。Microsoft的ODBC为各种类型的数据库管理系统提供了统一的编程接口。ODBC是一种使用SQL的程序设计接口。

Visual C++的MFC提供了几个数据库类，在利用ODBC编程时，经常用到 Cdatabase(数据库类)、CrecordSet(记录集类)和CrecordView(可视记录类)。

值得注意的是：在Visual C++中生成应用程序框架的视图类(Class view)时，包含一个指向操作数据库即Access文件的指针。该指针的目的是在视表单和记录集间建立联系，同时使历史数据的查询结果方便地在表单上显示出来。

用Microsoft Access创建1个Testing.mdb数据库，然后，在 View类中定义几个相关的重要变量。对于采集数据的曲线显示及报警直接采用编写的Active控件来实现具体的功能。主要是在WM_TIMER的消息处理函数OnTimer( )中调用数据显示函数以定时刷新数据。

1.1.4 软件系统主要功能

(1) 车用柴油机状态参数监测。实时检测信号主要以状态图、数据表格图等方式动态显示测量数据，当信号超过上限时，以红色在界面动态显示。该模块同时按不同的功率和热工状况对数据进行汇总，用于车用柴油机运行状况分析与诊断提供标准参数。对各传感器检测点的状态参数进行比较和整合，以调整到合理值。

(2) 车用柴油机振动特性分析。该程序块利用数据库参数对车用柴油机振动特征进行分析与识别，这对提高运行经济性、及时发现异常运行情况、指导运行人员操作维护很有帮助。

(3) 打印和报表。主要包括监测报表的生成、相关的数据打印。该功能较容易实现。

1.2 车用柴油机振动特征信号混沌识别特征参数

1.2.1 关联维数计算

1983年，Grassberger与 Procaccia提出了一种计算动力系统吸引子维数的方法，简称为 G-P算法[12]。此方法常用于资料点数不是很多的时间序列以及需计算高维行为的离散系统。定义相关积分函数Cm(ε)为：

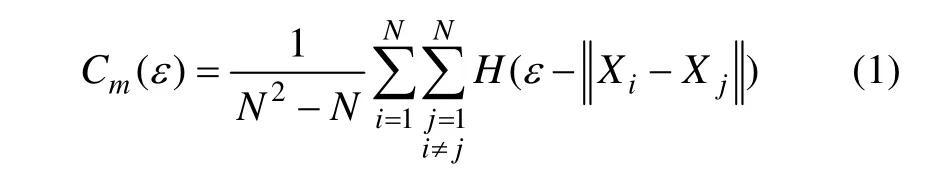
式中：ε为以Xi或Xj为区域中心的半径；‖Xi-Xj‖为Xi与Xj的欧氏距离；H为Heaviside阶跃函数，即

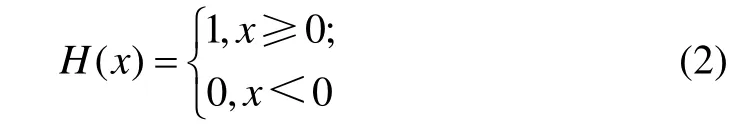
给定ε后，Cm(ε)表示2点间距离小于ε的概率，在适当的范围内，当ε增加时，

对式(3)两端同时取对数后成为：

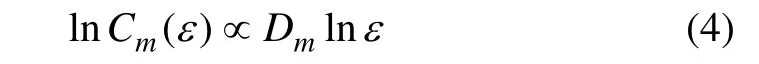
维数m的选择一般从小到大，不断增大其取值。针对某个m值，选取若干个不同的ε，分别计算相应的 Cm(ε)。将这些不同的 ε和 Cm(ε)代入式(4)可得到 lnε与lnCm(ε)的关系曲线。对于随机过程，Dm将随m的增加而增加，并不会达到饱和。但对确定性系统，Dm将在某一特定的m后趋于饱和(lnε与lnCm(ε)的关系图存在无标度区即直线段)，表明时序分布存在分形特征，且直线段的斜率就是吸引子的维数D2，与之相对应的嵌入维数为饱和嵌入维数 m∞。m∞表征系统自由度数目，它和D2分别给出了系统包含的基本变量数目的上限与下限。

1.2.2 Lyapunov指数计算

对于一维动力学系统，Lyapunov指数可表示为：

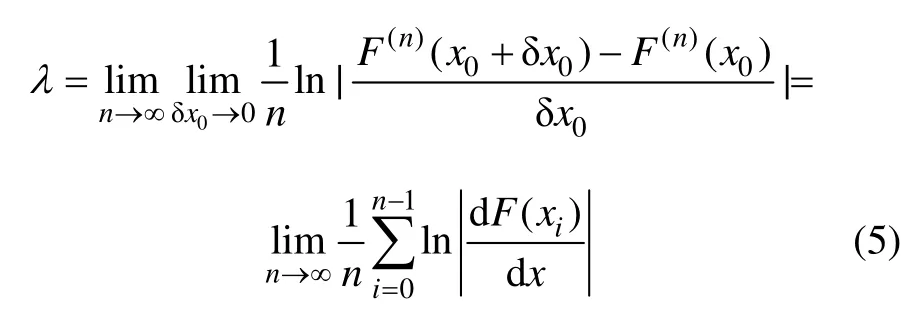
对于高维动力学系统，Lyapunov指数可表示为：

式中：||·||表示m维空间的距离。

1.3 实例应用

本文实验在4105型柴油机上进行。在转速为900 r/min、负荷为满负荷的75%时以15kHz采样频率测取500个含噪声的柴油机机身振动混合信号数据，通过EMD去噪声处理得到如图3所示的500个车用柴油机振动信号时间序列数据(其中，a为加速度，t为时间)。当嵌入维数m不同时，柴油机振动信号lnε与ln(Cm(ε))关系见图4。

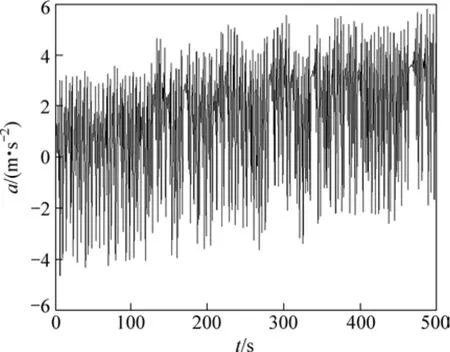
图3 车用柴油机振动信号时间序列Fig.3 Vehicle diesel engine vibration signals time series

为便于操作，对以上数据进行归一化处理，然后，通过对饱和关联维数进行计算。车用柴油机振动信号时间序列嵌入相空间维数m与关联维数D2的关系见图5。

从图5可见：当含噪声振动信号时间序列嵌入相空间维数m≥8时，关联维数(吸引子维)趋于稳定，即达到饱和关联维D2=0.868 62。

据混沌理论，车用柴油机振动系统内部影响机身振动信号变量的因素较多，最多可达8个，最少不会少于1个，可能包括：气体爆发压力、排气门开启时气体节流冲击、进气门落座冲击、排气门落座冲击、活塞换向时对缸套的冲击、燃烧激振、转速以及曲轴等运动件的回转运动等因素。因此，从这一意义上说，去噪车用发动机振动信号时间序列具有混沌特性。

图4 柴油机振动信号lnε-ln(Cm(ε))关系曲线Fig.4 ln(ε) and ln(Cm(ε)) of vehicle diesel engine vibration signals

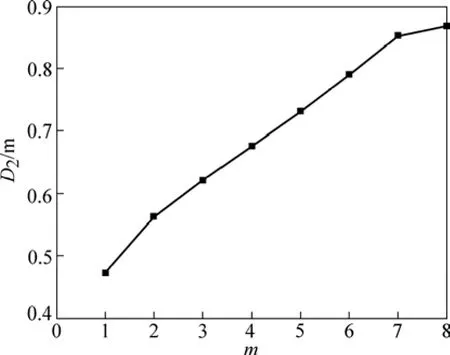
图5 车用柴油机振动信号时间序列嵌入相空间维数m与关联维数D2关系Fig.5 Relationship between embedded dimension and saturated dimension of vehicle diesel engine vibration signals time series

2 车用柴油机振动信号故障诊断系统应用

以4105型车用柴油机第2缸缸盖、缸套及机身振动信号为例进行说明。为进行标定，同时测量了第 2缸上止点信号。信号采样频率为25 kHz，柴油机转速为1 500 r/min，负荷为满负荷的50%，采用基于EMD和小波分析融合的车用柴油机振动信号去噪处理方法对振动信号进行去噪声处理。车用柴油机振动信号不但含有本缸激励力的信息，而且其他缸对其振动也有影响。为验证混沌及分形理论在4105型车用柴油机故障诊断中的应用，对第2缸排气门设置如表1所示的不同的故障(正常间隙为0.25 mm，进气门正常)，采集相应情况下的各种振动信号，计算信号的关联维数及李雅普诺夫指数，以便为4105型车用柴油机实现故障诊断。

图6所示为车用柴油机正常工况(状态2)下，缸盖、缸套及机身振动信号的时域波形。显然，振动信号是非平稳的。

由于测量的位置及激励力不同，3种振动信号的波形在时域上有一定的差别，幅值及位置差异也较大，其中包含柴油机工作状态信息，如气阀状态、气缸压力冲击力等。

2.1 关联维数计算结果

对实测的经去噪处理后的车用柴油机振动信号进行计算，通过10次平均，求得信号的关联维数如表2所示。

表1 排气门状态Table1 States of exhaust valves

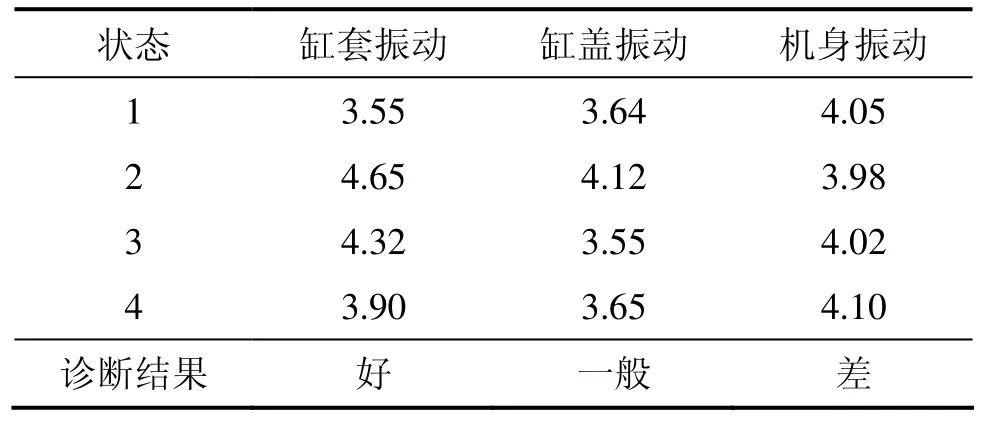
表2 m∞=10时车用柴油机振动信号关联维数D2Table2 Correction dimension number D2 of some vibration signals from vehicle diesel engine when m∞ is 10

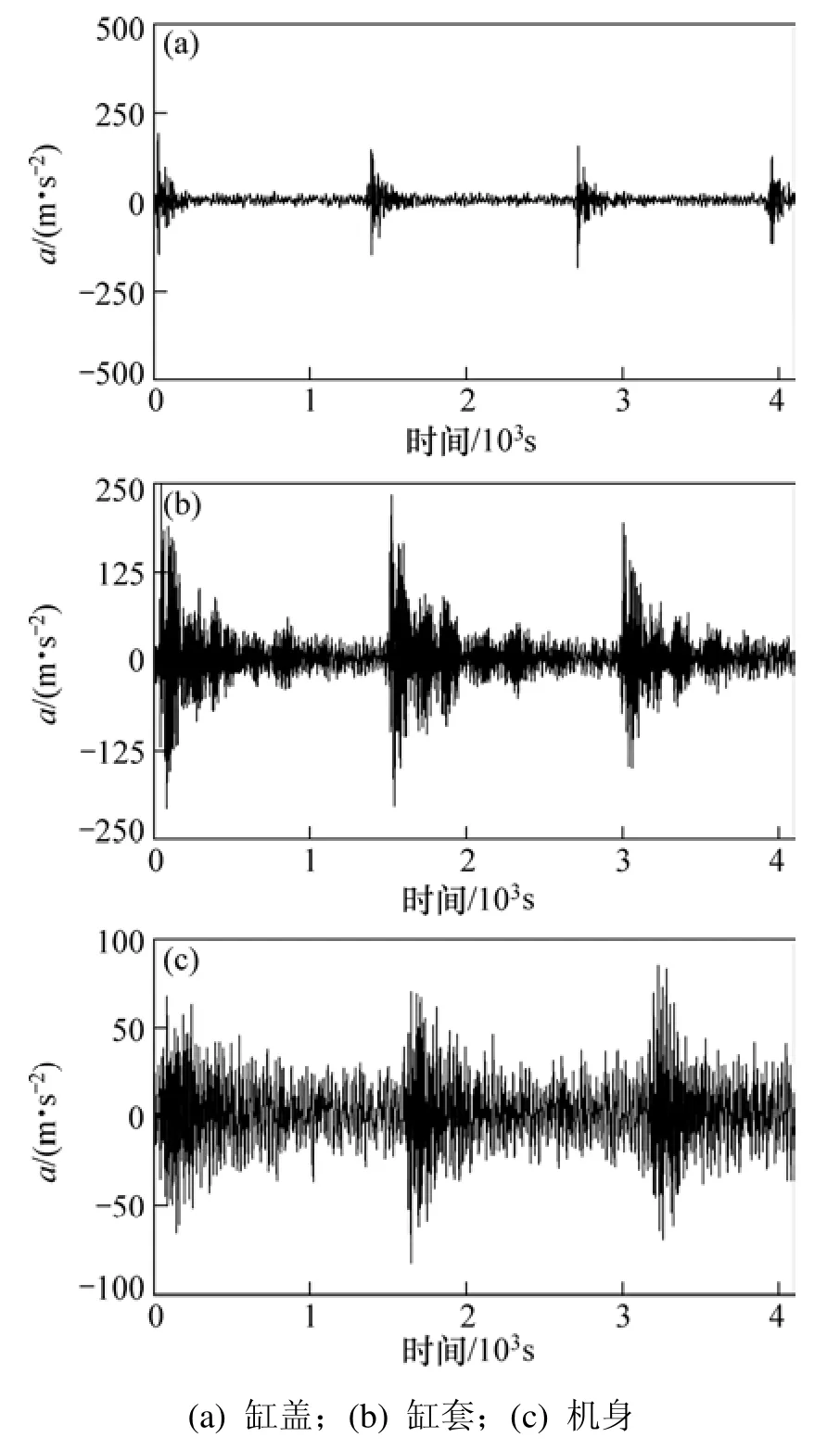
图6 车用柴油机振动信号Fig.6 Some vibration signals from vehicle diesel engine

从表2可以看出：3种振动信号的关联维数均为分数，具有一定的诊断能力，效果最好的为缸套振动信号的关联维数，其次是缸盖振动信号的关联维数；机身振动信号的关联维数的诊断能力最差。缸套振动主要由活塞横向撞击力引起，气阀机构状态变化时气门启闭时刻将改变，从而导致气缸工作状况发生变化，活塞横向撞击力也将随之改变，所以，在缸套振动信号中反而能较好地体现这一变化。本文中缸套磨损间隙为正常值，对缸套磨损严重等故障情况未进行研究。机身振动由于激励力传递路径较远，所以，计算的关联维数相差不大，导致诊断效果不好。本来缸盖振动信号的关联维数应该是最具有诊断能力的诊断特征量，因为气门状态的变化直接会在缸盖振动信号中体现出来，但由于气缸压力对缸盖振动的影响较大，当气门处于不同状态时导致计算的关联维数差别不是很明显。关联维数为分数也说明信号可能具有混沌特性。

分析缸盖振动信号的关联维数可以看出：当气门磨合良好时，缸盖振动信号的关联维数最大。这主要是因为这时“漏气作用力”对缸盖振动的贡献较小，缸盖的振动行为不确定因素最大，系统行为将在相空间趋于某一有限维吸引子或者奇异吸引子；而当气门处于故障状态时，关联维数将下降，此时，缸盖的振动行为在相空间趋于有限维的吸引子或奇异吸引子与正常状态时的相比是不同的。这主要是因为“漏气作用力”对缸盖振动的贡献明显大于磨合良好时的贡献，系统行为的不确定性减小，关联维数将减小，所以，关联维数下降意味着故障发生。这说明关联维数可以作为判断气门故障的特征量。

2.2 Lyapunov指数计算结果

各种振动信号的李雅普诺夫指数计算结果如表 3所示。

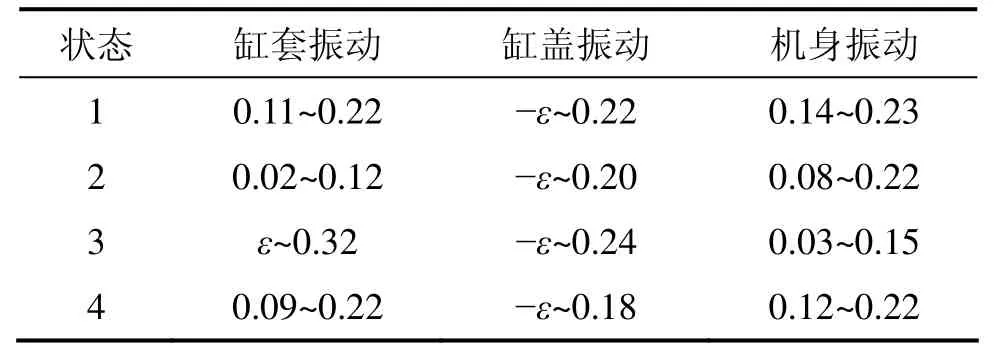
表3 0＜ε＜0.001时车用柴油机振动信号李雅普诺夫指数λTable3 Lyapunov index λ of some vibration signals from vehicle diesel engine when 0＜ε＜0.001

从表3可以看到：机身、缸套振动信号的李雅普诺夫指数基本均为正；缸盖振动信号的李雅普诺夫指数为负时的绝对值很小。从各种振动信号的李雅普诺夫指数可以看出：缸盖振动信号较缸套、机身振动复杂，规律性不强，即缸盖振动具有周期突变性，确定性与混沌特性共存，而缸套振动、机身振动可以认为是混沌振动。

3 结论

(1) 车用柴油机振动信号时间序列是混沌序列，具有非线性混沌动力系统演化特征；影响车用柴油机振动的系统内部因素最多可达 8个，最少不会少于1个。

(2) 车用柴油机各种振动信号具有混沌特征，但缸盖振动不能简单地认为是确定性混沌振动，而是确定性与混沌特性共存，在应用分形及混沌理论处理时需要注意。

(3) 车用柴油机振动信号的关联维数对气门机构的简易诊断具有一定的参考意义，可以作为1个诊断特征量。

[1] 张亮, 杜海平, 史习智. 基于小波分析的柴油机振动信号降噪处理[J]. 数据采集与处理, 2000, 15(4): 521-524.

ZHANG Liang, DU Hai-ping, SHI Xi-zhi. Noise reduction of cylinder vibration based on wavelet series[J]. Journal of Data Acquisition & Processing, 2000, 15(4): 521-524.

[2] Shigehiro U, Masaya O, Masahisa N. Noise and vibration reduction of newly developed 3.0l direct injection diesel engine[J]. JSAE Review, 2002, 23(3): 285-289.

[3] 黄强, 高世伦, 宾鸿赞, 等. 基于分形和神经网络的柴油机振动诊断方法[J]. 华中科技大学学报: 自然科学版, 2005, 33(9):68-70.

HUANG Qiang, GAO Shi-lun, BIN Hong-zan, et al. The method of vibration diagnosis for diesel engine based on the fractal theory and neural network[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2005, 33(9):68-70.

[4] Charles P, Sinha J K, Gu F, et al. Detecting the crankshaft torsional vibration of diesel engines for combustion related diagnosis[J]. Journal of Sound and Vibration, 2009, 321(3/5):1171-1185.

[5] Vakman D. New high precision frequency measurement[J].Measurement Science and Technology, 2000, 11(3) 1493-1497.

[6] Gu F, Yesilyurt I, Li Y, et al. An investigation of the effects of measurement noise in the use of instantaneous angular speed for machine diagnosis[J]. Mechanical Systems and Signal Processing, 2006, 20(6): 1444-1460.

[7] Carlucci A P, Chiara F F, Laforgia D. Analysis of the relation between injection parameter variation and block vibration of an internal combustion diesel engine[J]. Journal of Sound and Vibration, 2006, 295(1/2): 141-164.

[8] 王德智, 夏军, 张利平. 东北地区月降雨时间序列的混沌特性研究[J]. 水电能源科学, 2002, 20(3): 32-34.

WANG De-zhi, XIA Jun, ZHANG Li-ping. Chaos analysis of monthly precipitation time series in North-east China area[J].Hydroelectric Energy, 2002, 20(3): 32-34.

[9] E Jia-qiang, MEI Chi. Chaotic behavior of crude copper composition time series in the process of matte converting and its predicable time scale[J]. Nonlinear Analysis: Real World Applications, 2006, 7(4): 651-661.

[10] Abarbanel H D I, Brown R, Sidorowich J J, et al. The analysis of observed chaotic data in physical systems[J]. Rev Mod Phys,1993, 65(4): 1331-1392.

[11] Rosenstein M T, Collins J J, DeLuca C J. Reconstruction expansion as a geometry-based framework for choosing proper delay times[J]. Physica D, 1994, 73: 82-98.

[12] WEI En-bo, TIAN Ji-wei, XU Ji-shan. New method to obtain the power spectra of hidden variables and its application to ocean data[J]. Chinese Journal of Oceanology and Limnology, 2001,19(1): 29-34.