相似原理应用于混响室缩比模型的验 证 分 析
2011-05-29齐万泉汪宗福马蔚宇杨于杰
齐万泉 汪宗福,2 马蔚宇 杨于杰
(1.北京无线电计量测试研究所,北京 100143; 2.中国三江航天集团设计所,湖北 武汉 430035)
1.引 言
混响室不同于常规均匀场的试验方法,以易于实现高场强等诸多优点在电磁兼容测量领域受到高度重视并逐渐得到相关标准化组织和实验室的接受[1-2]。国内相关单位也逐渐加快了混响室的建设与研究[3-4]。
由于大型混响室建造成本高、风险大,所以大型混响室在建造前总希望通过各种方法来评估建成后的性能,降低建设风险。通过对缩比模型性能的测试预估大型混响室性能是一种方法,但是该方法是否可行需要进行验证分析。这种将混响室缩比模型应用于大型混响室设计的思想来源于电磁场相似原理[5]。电磁场相似原理通常应用于辐射或散射等开场问题,其推导基于无源问题。混响室是一种金属谐振腔模型。相似原理是否适用于混响室这种有源谐振腔模型有待于进一步证明。
由于混响室腔体内部场分布复杂,目前还未见有公开发表文献介绍这种有源谐振腔的解析解,也没有混响室有源激励电磁场的解析解。对于混响室模型的分析通常基于统计模型[6-8]的基础上。
为了说明相似原理在混响室缩比模型中的适用性,从理论推导、仿真分析及试验验证三个方面进行论证,证明了大型混响室与其缩比模型性能的一致性。
2.理论分析
首先从电磁场相似原理推导和混响室中的模式分析两个方面说明相似原理在混响室模型中应用的可行性。
2.1 电磁场相似原理
相似原理是保证模型实验与真实现象相似并将实验结果转换到实物上的理论。对于某一物理现象相似时,表征该现象特征的所有物理量必然各自保持一定的比例关系。对于电磁场问题,如果希望某两个问题具有同样的场分布,则可能通过保证两个问题的波长和几何尺寸成一定比例关系实现,即保证电尺寸这一无量纲数恒定不变。
对于空间某两个无源区域,电磁场均满足麦克斯韦方程
(1)
式中:E、H分别为电场和磁场强度;ε、μ、σ分别为介电常数、磁导率和电导率;ω为角频率。
如果令两个区域介质特性相同,即ε、μ、σ保持不变,且两区域对应长度和计算频率分别保持比例关系,即
r2=β1r1,ω2=β2ω1
(2)
式中:r1,r2分别为两个区域的长度;ω1,ω2分别为两个区域的计算角频率;β1,β2分别为比例系数。
如果需要两个区域的场分布相同,则有
E1=E2,H1=H2
(3)
由式(1)、(2)、(3)可得
β1β2=1
(4)
由此可见,在一般无源问题中,若能保持介质电特性参数ε和μ不随角频率ω变化,则计算频率与计算区域物理尺寸的乘积只要保持不变,即电尺寸保持不变,电磁场分布就维持不变。从场分布的角度看,用混响室缩比模型进行设计是可行的。
2.2 混响室中的模式分析
对于开域问题应用电磁场相似原理是没有任何问题的,但是混响室内模式丰富,场分布复杂,电磁场相似原理是否适用有待证明。由于衡量混响室场性能的一个重要指标为空间中的场均匀性。混响室中的均匀性[9-10]与在腔体内的模式数有着重要的联系,从混响室模式分析考虑,相似原理仍然可应用于混响室的缩比模型。
对于三维尺寸分别为a、b、d的矩形腔体,其谐振频率可由式(5)计算。
(5)
式中:fmnp为谐振频率;c为光速;m、n、p为不小于零的整数。
当混响室腔体缩小x分之一时,由式(5)可知,同一m、n、p下谐振频率会增加x倍。
文献[11] 分析了矩形腔体中存在的模式分布。在理想金属边界条件下,混响室中的模式成分有五种可能的情况,如表1所示。
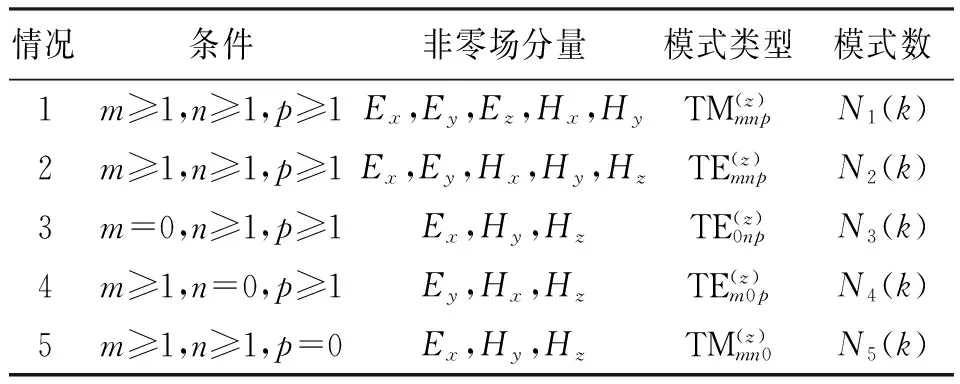
表1 本征模场分量
混响室中模式数总和为
N(k)=N1(k)+N2(k)+N3(k)+
N4(k)+N5(k)
(6)
经过计算可得到模式数的计算公式为
(7)

总模式数可以划分为平稳部分为Ns(f)和波动部分Nf(f)。平稳部分由式(7)右边第一项计算,波动部分由式(7)右边后两项计算。将k的表达式带入式(7),可得平稳部分计算公式
(8)
由式(8)可知,模式数平稳部分满足相似原理,在混响室腔体几何尺寸缩小为原来的x分之一,工作频率提高x倍时,模式数平稳部分的值保持不变。
由式(7)可知,模式数波动部分并不满足腔体几何尺寸与工作频率的相似原理。但是波动部分的模衰落很快,它与模式的简并有关,当腔体边长比为有理数时,将会出现很多简并情况,即不同的(m,n,p)组合对应同一个谐振频率,当边长比为整数时,简并情形将出现更多,模分布将很不均匀。在混响室设计时应尽量避免简并模的出现,降低模式数的波动部分。当混响室腔体几何尺寸比例关系为无理数并且工作在一定频率以上时,混响室的总模式数与平稳部分的模式数基本一致,因此可认为混响室腔体的模式数满足相似原理。
根据混响室场分布的特点,模式数是影响混响室场均匀性的重要指标,混响室缩比模型的模式数与缩比前模型满足相似原理,说明缩比前后混响室的场均匀性性能是可比拟的。
3.仿真结果分析
为了验证相似原理在混响室缩比模型的适用性,首先建立了腔体A(2 m×1.4 m×1.1 m)和腔体B(0.2 m×0.14 m×0.11 m)的模型,两个模型三维尺寸相差十倍。对腔体A,用1 GHz的振子天线作为发射天线,考察坐标点M(0.5 m,0.3 m,0.3 m)的场强值。对腔体B,用10 GHz的振子天线作为发射天线,考察坐标点N(0.05 m,0.03 m,0.03 m)的场强值。A和B两个腔体模型中,天线位于腔体中心位置,天线中心与坐标原点重合,电场探头放置于需要考察的M点和N点。振子天线仿真模型如图1所示。天线放入腔体后仿真模型如图2所示。
图3为1 GHz频点和10 GHz频点的半波振子天线在自由空间的VSWR仿真结果。结果显示在自由空间中半波振子天线满足相似原理。
图2 放入天线的腔体模型
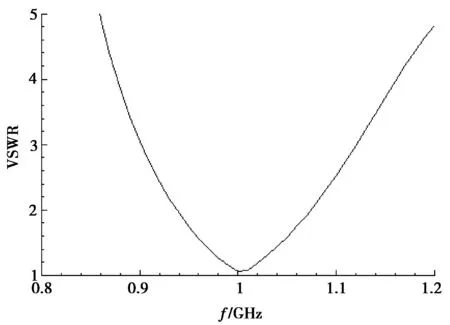
(a) 1 GHz

图1 半波振子天线仿真模型
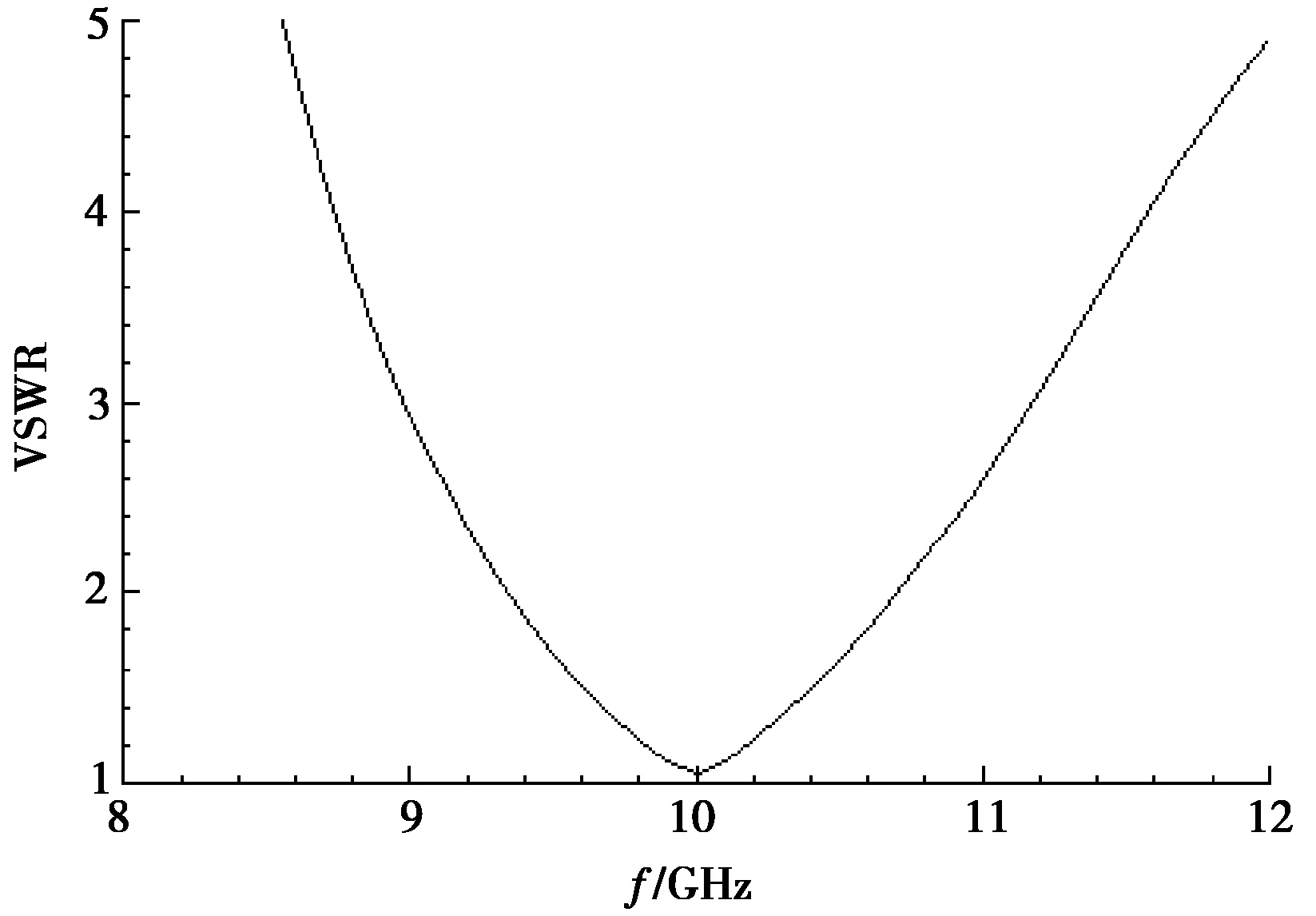
(b) 10 GHz图3 半波振子天线VSWR
表2给出了1 GHz振子天线在自由空间及腔体A中M点的场强值,同时给出了10 GHz振子天线在自由空间及腔体B中N点的场强值。结果显示,无论是自由空间中还是腔体中1 GHz频点下M点的场强值都基本等于10 GHz频点下N点场强值的十分之一。这与天线在远场区电场值与距离成反比的规律是一致的。该结果表明,将天线置于金属腔体后,在距离天线一定距离的位置处电场值满足相似原理。
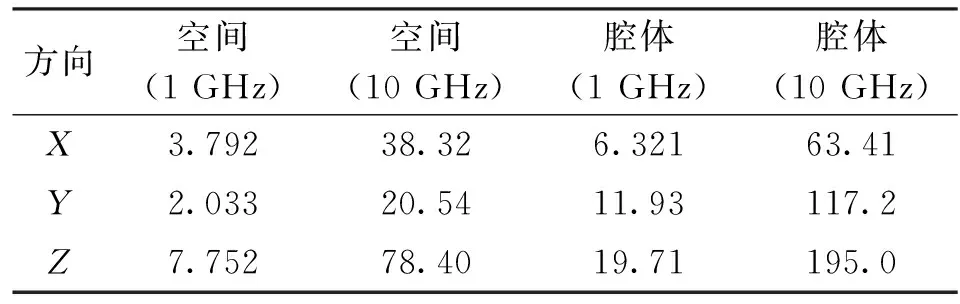
表2 电场探头场强值(单位:V/m)
在进行了简单半波振子天线在腔体中某固定位置的电场值仿真分析之后,对简单的混响室模型进行了建模并仿真分析了场均匀性的标准偏差指标,混响室原型和缩比模型采用10∶1的比例进行建模。混响室原型的尺寸为10.5 m×6.4 m×4.6 m,其最低工作频率为100 MHz,缩比模型的尺寸为1.05 m×0.46 m×0.64 m,其最低工作频率为1 GHz。混响室内的天线采用振子天线。模型如图4所示,振子天线位于混响室左后部,搅拌器位于混响室前部,箭头为矩形工作区域八个顶点放置的电场探头。
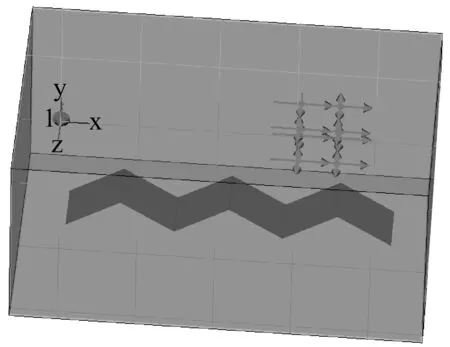
图4 混响室模型
根据混响室原型和缩比模型的对应关系,对混响室原型在100~150 MHz频段内选择六个计算频点,步进10 MHz,缩比模型在1~1.5 GHz中选择六个计算频点,步进100 MHz。通过仿真得到混响室缩比前后场均匀性标准偏差,结果如表3所示。
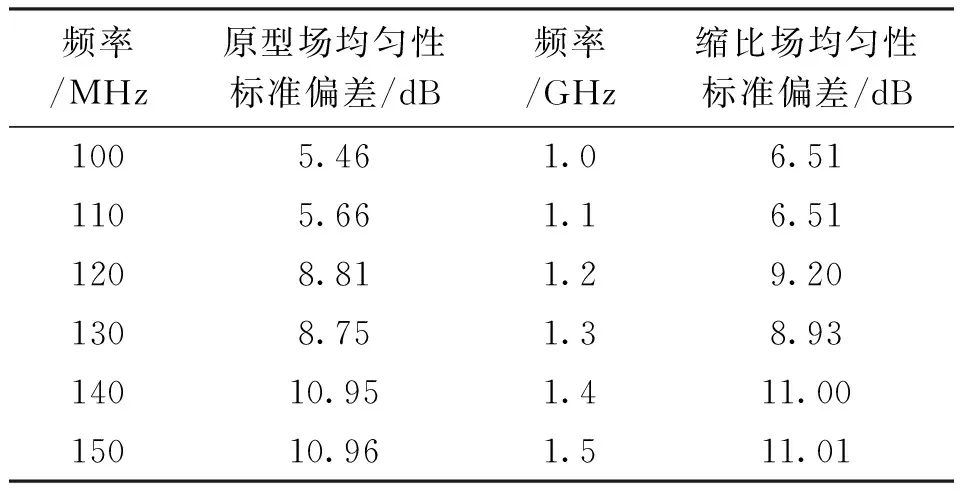
表3 混响室原型和缩比模型场均匀性
从表3中可以看到,混响室原型从100~150 MHz的场均匀性标准偏差变化趋势和缩比模型从1~1.5 GHz的场均匀性标准偏差变化趋势一致,而且随着频率的升高,原型和缩比模型之间的差距越来越小,结果越来越吻合。这从场均匀性的角度验证了缩比模型和原型之间的场性能基本一致,从而为利用缩比模型设计大型混响室的可行性提供了有力支撑。
4.仿真方法试验验证
为了验证仿真分析方法的正确性,对现有的混响室进行了试验验证和仿真分析。仿真模型如图5所示,场均匀性标准偏差测试与仿真结果比较如图6所示。
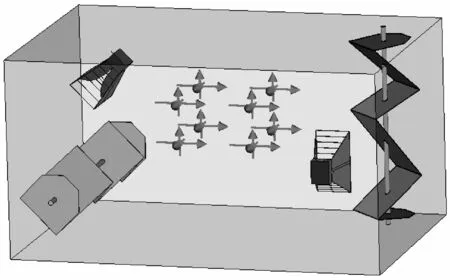
图5 SMART-1000混响室仿真模型
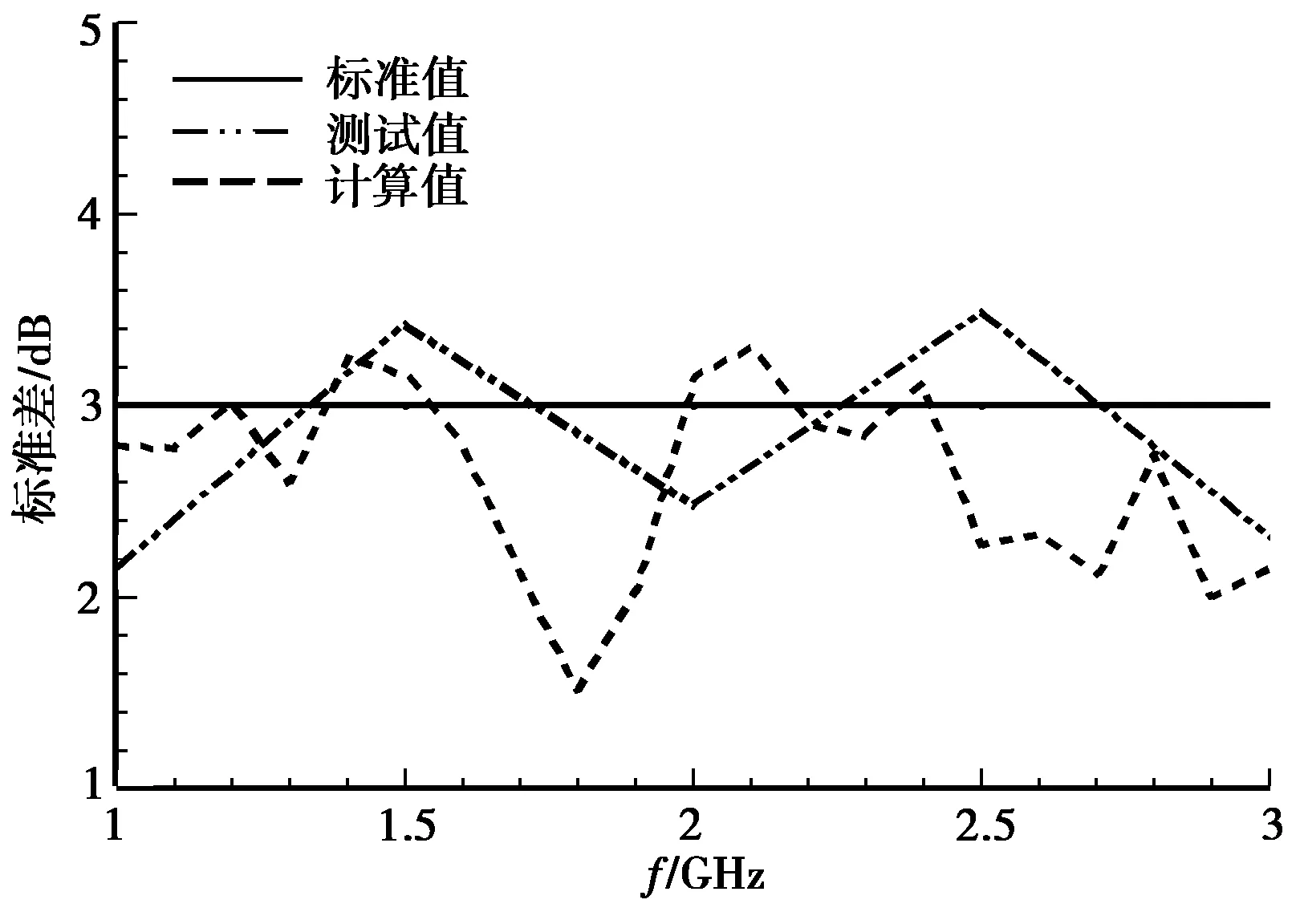
图6 混响室场均匀性测试与计算结果比较
从图6中可以看到,混响室的测试结果和计算结果是能够比拟的,说明了仿真分析所得到的结果是可信的。
5.结 论
利用相似原理将缩比模型应用于大型混响室的设计,可以利用缩比模型大体上推算和估计出大型混响室的场性能特性。从这个思路出发,证明了相似原理应用于混响室腔体模型的可行性,说明了利用缩比模型进行大型混响室设计的思路和方法是可行的,它将有效地降低混响室设计成本和设计风险、提高设计效率和设计水平。
根据分析和比对,可以发现,要想通过缩比模型的场性能推测大型混响室的场性能特性,必须在缩比过程中具备以下条件:
1) 混响室原型与缩比模型需要几何相似,除外形相似外,内部搅拌器及仪器布置也需要相似。
2) 当混响室模型尺寸缩小x分之一时,缩比模型工作的波长也应该缩小x分之一,工作频率提高x倍。
3) 当缩比模型工作频率提高x倍后,所使用的测试设备需要更换为相应的工作频段。
当然,在实际的设计过程中,缩比前后一些条件难以达到完全相似,如腔体材料只能使用有限电导的金属材料,腔体内部无法理想光滑,不同频段的天线性能并不相似,大型混响室需要加装更多的附属设施,这些因素都对混响室的场分布造成一定影响,但是在混响室设计中,全面考虑这些因素对场性能的影响,尽量采用高导电材料,内部尽量光滑,混响室的场均匀性能指标是能够得到保证的。
[1] IEC 61000-4-21, EMC Part 4-21: Testing and measurement techniques-Reverberation Chamber Test Methods[S]. International Electrotechnical Commission(IEC), Geneva, Switzerland Int. Std. CISPR/A and IEC SC 77B, 2007.
[2] RTCA DO-160F: Environmental conditions and test procedures for airborne equipment[S]. RTCA, Inc. Washington, DC. USA, Dec, 2007.
[3] 袁智勇, 李 暾, 陈水明, 等. 混响室设计与校准测试[J]. 电波科学学报, 2007, 22(4): 571-576.
YUAN Zhiyong, LI Tun, CHEN Shuiming. Design and calibration of reverberation chamber[J]. Chinese Journal of Radio Science, 2007, 22(4): 571-576. (in Chinese)
[4] 丁坚进, 沙 斐. EMC混响室电磁场模态研究[J]. 电波科学学报, 2005, 20(5): 557-560.
DING Jianjin, SHA Fei. Analysis of electromagnetic mode-states in an EMC reverberation chamber[J]. Chinese Journal of Radio Science, 2005, 20(5): 557-560. (in Chinese)
[5] 苏东林, 陈爱新, 谢树果, 等. 电磁场与电磁波[M]. 高等教育出版社, 2009: 492-494.
SU Donglin, CHEN Aixin, XIE Shuguo, et al. Electromagnetic field and wave[M]. Higher education press, 2009: 492-494. (in Chinese)
[6] KOSTAS J G, BOVERIE B. Statistical model for a mode-stirred chamber[J]. IEEE Transactions on Electromagnetic Compatibility, 1991, 33(4): 366-370.
[7] CORONA P, FERRARA G, MIGLIACCIO M. Reverberating chambers as sources of stochastic electromagnetic fields[J]. IEEE Transactions on Electromagnetic Compatibility, 1996, 38(3): 348-356.
[8] HILL D A. Electromagnetic theory of reverberation chambers [R]. NBS Technical Note 1506, 1998
[9] WANG Y J, KOH W J, TAI Y K, et al. Evaluating field uniformity of a mini-reverberation chamber with two mechanical stirrers[C]//IEEE International Symposium on Electromagnetic Compatibility, Aug, 2002: 795-798.
[10] ASANDER H J, ERIKSSON G, JANSSON L, et al. Field uniformity analysis of a mode stirred reverberation chamber using high resolution computational modeling[C]//IEEE International Symposium on Electromagnetic Compatibility, Aug, 2002: 285-290.
[11] LIU B H, CHANG D C. Design consideration of reverberating chambers for electromagnetic interference measurements[C]//IEEE International Symposium on Electromagnetic Compatibility, Aug, 1983: 508-512.
