变电站二次设备全寿命周期费用与可靠性关系模型

黄 莉，张雪松，杨卫星

（1.浙江同济科技职业学院，杭州 311231；2.浙江省电力试验研究院，杭州 310014；3.浙江大学电气工程学院，杭州 310013；4.浙江省电力设计院，杭州 310012）

0 引言

目前，国家电网公司正在全面推进变电站设备的LCC（Life Cycle Cost，全寿命周期费用）管理工作。在设备初始选型阶段，将不仅仅考虑其购置成本，还计及运行维护、退役等成本，从全寿命周期费用的角度对设备进行评价。从用户的角度出发，希望设备可靠性高且全寿命周期费用尽量低，但在实际中，这个目标却难以实现，因为高可靠性的要求必然带来厂家的高投入，设备价格也将相应提高。因此，如何在设备可靠性和全寿命周期费用之间进行权衡是目前亟需解决的问题。文献[1-5]针对变电设备的可靠性问题进行了研究；文献[6-9]则研究了变电站变压器、GIS等一次设备寿命周期费用管理问题。这些成果均未对变电站二次设备如何在可靠性基础上进行全寿命周期成本控制进行系统分析。

本文从分析设备LCC与可靠性关系的模型入手，在保证系统可靠性的前提下，通过让年平均费用达到最小来实现变电站二次设备LCC的最优化，为解决变电站二次设备管理中存在的问题开辟了一条新途径。

1 设备寿命周期费用定义及计算方法

设备的寿命周期是指设备从论证开始到退役为止所经历的全部时期，一般可分为论证、方案、工程研制、生产、使用及退役6个阶段。设备的寿命周期费用则是指在设备整个寿命周期内各个阶段所需支付的费用总和。电力公司是设备使用者，一般不参与生产和科研，因此，电力公司对设备进行全寿命周期费用分析时，按照二次设备寿命周期的运行规律，将设备标准运行状态及关键控制点作为全过程管理的重点，依据LCC理论并根据变电二次设备的相关费用支出情况构建相应的计算模型：

式中：LCC为全寿命周期费用；CB为购置费，包括采购费用和安装时花费的运输、人工、调试等费用；CR为运行维护费，即为了保证设备正常运转而发生的费用，包括运行费用以及在寿命期内检修、维护、试验等所需要的材料费、人工费和交通费等维护费用；CD为退役处置费用，即变电设备退役后拆除、运输等费用。

设备的全寿命周期管理就是在满足可靠性、安全性的前提下，以LCC最小为目标的管理方法。因此，LCC的估算是全寿命周期管理工作最基础、最重要的工作。

目前，LCC的估算方法有工程估算法、类比估算法、参数模型估算法和专家判断估算法[10]。

（1）工程估算法

工程估算法是最传统的LCC估算法，依据LCC的分解结构，对设备在购置、使用维护及报废等不同阶段的各个环节和过程中需支出的费用加以测算，逐项叠加后得出整个系统各阶段的总费用，最后集成为寿命周期费用，其特点是详尽、具体、繁琐、费时，但精度较高，可达90%。

（2）类比估算法

类比估算法一般用于新研制设备与现有设备具有类似功能、且其结构和性能特征与现有设备又是可比的情况。将新研制设备与现有设备（已有准确费用数据和技术资料）在技术、使用与维护方面进行比较，分析两者的异同点及其对费用的影响，根据经验判断求出新研制设备相对于现有设备的费用修正方法，再计算出新研制设备的费用估计值。

该方法适用于研制的早期阶段，在不能采用参数估算法和工程估算法时使用，也经常用于验证参数估算法的估算结果。利用该方法可以估算寿命周期费用或某项主要费用和单元费用，或者某一个主要分系统或设备的费用。

对现有系统各有关费用作有针对性的修正（即考虑到配置上的差异），即可得到新系统所需费用。但是这种修正主要凭借经验，误差较大，所以很少独立使用。

（3）参数模型估算法

参数模型估算法是利用同类设备历史统计数据导出的数学关系来估算新设备费用的方法，即利用汇集起来的具有类似用途的硬件与软件的现有大量数据库，仅用系统少量设计参数或特征量来表达费用的参数方程，然后把一系列费用估算关系方程有机地编排和组合在一起，构成费用模型，通过计算机处理，即可得出相应的费用。

费用估算关系式可能很简单，也可能很复杂，即可反映设备研制、生产和使用维护费用，又能反映这些费用的个别部分或几个部分的组合。因此，系统级或分系统级均可采用此法来估算费用。

参数模型估算法特别适用于设备招标计划的早期阶段。该方法要求输入的参数少，估算快，费用省，因此有助于分析各种选型方案变化时的费用。其估算精度取决于基本费用数据的质量和预期的外推精度。但是，由于新的设备在技术、生产工艺、采购策略、生产率或工业基础等方面都将发生很大变化，不易把历史统计数据调整到统一的基础上，因此系统级的估算精度不高，而分系统级由于有更多的技术数据输入，其精度预计可以达到很高。

（4）专家判断估算法

专家判断估算法是由专家根据经验估算设备寿命周期费用的方法，可由多个专家分别独立估算，再加以综合，以提高估算精度。一般在数据不足或没有足够的统计样本以及难以确定参数费用的关系式时使用，或用于辅助其它估算方法。

2 二次设备可靠性与LCC关系模型

系统可靠性对LCC有很大影响，主要体现在：购置费CB依赖于可靠性指标的高低，可靠性指标的高低对运行维护费CR产生重大影响，主要体现在对CB和CR的影响呈现两种相反的趋势。可靠性的提高即产品成本提高，导致CB不断提高，而CR却大幅度降低；可靠性较低，即CB降低，但CR却要升高。设备退役处置费则可认为是一常数。因此LCC将呈“浴盆”曲线，如图1所示，因而存在一个可靠性优化区域，即图1中R1与R2之间的区域。可靠性并不是越高越好，而应以LCC最低为目标，因此，在考虑可靠性与LCC关系时，应遵循合理性、方便性的原则。选用故障率λ作为参与因子，式（1）中认为CD是与可靠性无关的常数，因此主要考虑购置费CB和运行维护费CR与λ的关系。

图1 寿命周期费用LCC与可靠性R关系曲线示意图

对某指定设备来说，当考虑可靠性对相关费用的影响时，设其它说明性的变量与可靠性不相关，作为常数处理，即：

式中：C为相关费用；λ为故障率；K，β与λ无关，是待定系数。

设购置费 CB=fB（λ）=K1·[φB（λ）]α， 如果要求故障率很低，厂家的设计、研制及试验的费用将增加，设备的购置成本很高如果只要求很低的可靠性，则购置费会很低，也就是说 fB（λ）应满足：

显然fB（λ）为减函数， 且K1， α 为与 λ 无关的正常数，因此φB（λ）≥0且为关于可靠性R的增函数， 也满足根据函数论，φB（λ）满足上述两个条件的最简单的形式为：

对于检修费用CR，情况则有些不同，它不仅与 λ有关，而且和时间t有关，即CR=fR（λ）·t=K2·[φR（λ）]β·t。fR（λ）应满足：

φR（λ）≥0且为关于 λ 的增函数，K2， β 为与λ无关的正常数，其满足条件的最简单形式为：

将式（4）、 （6）代入式（1）得：

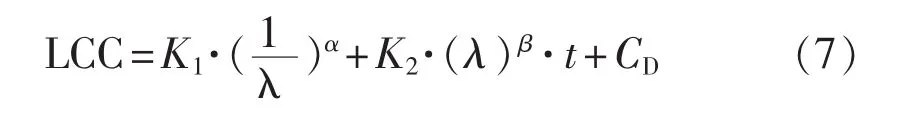
式（7）中K1， K2， α， β 是待定系数， 可通过回归分析来确定，主要步骤为：

（1）可靠性数据、全寿命周期费用的收集、分析整理。

（2）将式（7）的非线性方程线性化，主要方法是两端取自然对数，方程转化为关于lnK1，lnK2，α，β的线性方程。

（3）利用可靠性数据、寿命周期费用数据，通过线性回归方法（如最小二乘回归）来给出K1，K2，α，β的值。

3 设备寿命周期费用优化

由式（7）可知，设备的LCC是与MTBF（平均无故障时间）和服役时间t都相关的函数，而在考虑LCC最优时，还需要将其归算到同一时间间隔下才有意义，因为服役时间越长，其LCC越高，但平均到每年，其平均费用不一定高。因此，本文引入年平均费用YC的概念，通过实现YC的最优，来实现LCC的最优化。

首先考察在给定λ时，YC随时间t的变化规律， 由式（8）得：

可见，此时YC是关于t的减函数，也就是说，在设备寿命范围内，服役时间越长，年平均费用越低。电子产品的寿命取决于其薄弱部件的寿命，以保护产品为例，典型设计寿命一般都≥10万h，不考虑技术升级的因素时，其服役时间可选择接近其寿命值。

当设备的服役周期t0给定时，考察YC随时间λ的变化规律，对式（8）两边关于λ求导，得：

转化成平均无故障工作时间：

在实际应用中，求得的MTBFopm不一定符合一次系统对二次设备可靠性要求，此时则应按系统要求确定MTBF，以保证可靠性前提下的费用最优。

4 结语

在深入分析设备寿命周期费用与可靠性关系的基础上，给出了一种可靠性与LCC的关系模型，并通过引入平均年费用YC，对故障率一定和服役时间一定两种情况下的费用优化作了深入探讨。本文给出的模型在实际应用中还会遇到较多的问题，需要在实践中不断完善。

[1]张雪松，吴志力，程晓东，等．基于环境应力分析的变电站二次设备可靠性评估[J]．浙江电力，2009（3）：16-19．

[2]邱仕义．电力设备可靠性维修[M]．北京：中国电力出版社，2004．

[3]郭永基．电力系统及电力设备的可靠性[J]．电力系统自动化，2001，33（17）∶53-56．

[4]丁坚勇，邓瑞鹏，李江．发电设备的检修策略及可靠性管理研究[J]．电网技术，2002，26（3）∶72-75．

[5]殷天雷，史进渊．发电设备可靠性与设备检修管理策略的研究[J]．动力工程，2001，29（4）∶1303-1305．

[6]郭基伟，谢敬东，唐国庆．电力设备管理中的寿命周期费用分析[J]．高压电技术，2003，29（4）∶13-15．

[7]姚明，陈红兵，李莉华，等．全寿命周期成本（LCC）方法在500 kV地下变电站GIS采购中的应用[J]．中国电力，2008，41（8）∶32-34．

[8]姜益民，马骏．变压器的全寿命周期成本分析[J]．变压器，2006，43（12）∶30-34．

[9]李璐．电力一次设备全寿命周期组合化管理模式及实施[J]．供用电，2009，26（2）∶13-15．

[10]李向荣，郭广生，徐宗昌．武器装备寿命周期费用估算方法研究[J]．科技导报，2008，26（15）∶84-88．