遗传算法优化模糊控制器参数的方法研究

郭荣艳，史水娥

（1.周口师范学院 物理与电子工程系，河南 周口 466001；2.河南师范大学 物理与信息工程学院，河南 新乡 453007）

模糊控制[1-2]适合于数学模型未知，动态过程变化大的系统[3]。模糊控制不需要建立控制对象的精确数学模型，其基于专家经验和知识推理的智能控制方法具有很强的鲁棒性，通过选定合适的模糊控制规则，可在保证控制稳定的同时，保持较好的控制性能。因此它能绕过对象的不确定性、干扰及非线性、时变性、时滞性等影响，并且能够处理不确定信息，达到控制的要求与目的。

遗传算法[4]（Genetic Algorithm，简称GA）是一种解决复杂问题的有效方法，是基于进化论、在计算机上模拟生命进化机制而发展起来的一门新兴学科，它根据适者生存、优胜劣汰等自然进化规则来搜索问题的解。遗传算法的基本思想是从一个代表最优化问题解的种群开始进行搜索，通过若干代的进化最终得出条件最优的个体。遗传算法的优势在于求解最优化问题的全局最优解。算法的突出特点是它包含了与生物遗传及进化很相像的步骤：选择、复制、交叉、重组和变异。

本文在设计模糊控制器的基础上，基于遗传算法对该控制器的参数进行寻优，得到了最优的模糊控制系统。

1 模糊控制器的设计

本文选择二维模糊控制器。典型的二维模糊控制器的设计通常包括以下4个组成部分。

1）模糊化[5]采用正态分布确定模糊变量的赋值表，将误差和误差变化量的精确量转化成模糊量；

2）模糊推理 按照IF-THEN语言规则进行模糊推理，求出系统全部模糊关系所对应的控制规则并置于规则库；

3）模糊判决 用“最大隶属度法”、“加权平均判决法”等方法得到控制参数的模糊量；

4）去模糊化 把模糊判决后的结果由模糊量转化成为可以用于实际控制的精确量。

模糊控制系统的原理框图如图1所示。

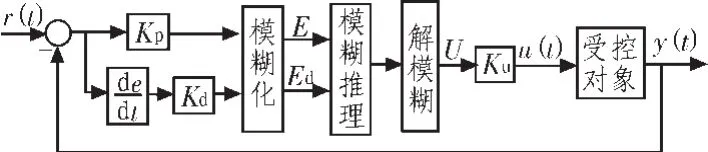
图1 模糊PD控制器控制框图Fig.1 Block diagram of fuzzy PD controller

模糊控制的性能取决于隶属函数[6]和推理规则。本文采用8段模糊子集的定义，和7段模糊子集的方式相比，这样的定义将ZO集合进一步细化为NZ（负零）和PZ（正零）两个子集，能更好的刻画0附近误差及其变化率的情况。误差E及误差变化量EC的模糊隶属度函数如图2所示。

图2 8段模糊子集示意图Fig.2 8 Schematic diagram of fuzzy sets

模糊控制规则的设计原则是：当误差较大时，控制量应当尽可能地减小误差；当误差较小时，除了消除误差以外，还考虑到系统的稳定性，以避免不期望出现的超调和振荡。模糊规则如图3所示。模糊推理规则的三维曲面如图4所示。

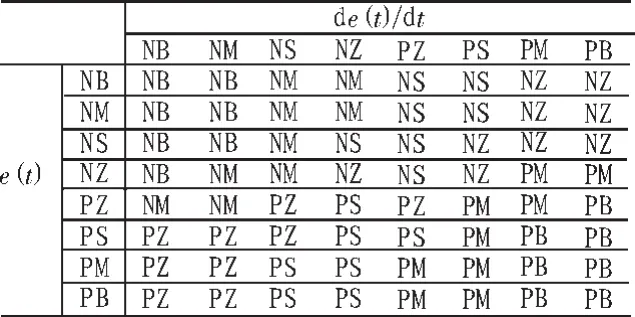
图3 模糊规则Fig.3 Fuzzy rules

图4 模糊推理规则的三维曲面表示Fig.4 Three-dimensional surface of fuzzy inference rules

2 模糊控制器的仿真

图5 模糊控制系统仿真模型Fig.5 Simulation model of fuzzy control system

当其中 a=5；Kp=2；Kd=1，Ku=1时，仿真结果如图6所示。

图6 模糊控制器的输出仿真结果Fig.6 The output simulation results of fuzzy controller

由仿真结果可知，运用模糊控制器，计算值的误差较小，上升速度快，可以较好地抑制超调的影响，消除了静态误差，具有良好的动态响应和静态特性。同时，由于采用了模糊推理，可以利用更多的经验规则，不断修正规则库，使系统在应用中可不断提高精度，优化控制性能。

3 基于遗传算法优化

遗传算法的一般流程如图7所示。

Step1：初始化群体；

Step2：计算群体上每个个体的适应度值；

Step3：按由个体适应度值所决定的某个规则选择将进入下一代的个体；

Step4：按交叉概率进行交叉操作；

Step5：按变异概率进行突变操作；

Step6：没有满足某种停止条件，则转step2，否则进入step7；

Step7：输出种群中适应度值最优的染色体作为问题的满意解或最优解。

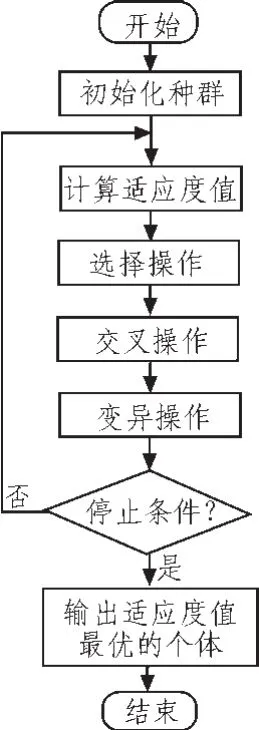
图7 遗传算法流程图Fig.7 Flow chart of genetic algorithm

遗传算法中的优化准则，一般依据问题的不同有不同的确定方式。例如，可以采用以下的准则之一作为判断条件。

1）种群中个体的最大适应度超过预先设定值；

2）种群中个体的平均适应度超过预先设定值；

3）世代数超过预先设定值。

本文选择ITAE准则指标为最优化指标，即时间乘绝对误差积分准则，该指标反映系统的综合性能，表达式如式（1）。 仿真模型如图8。

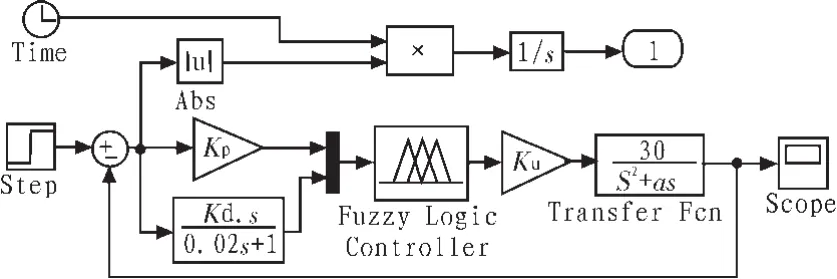
图8 最优控制仿真框图Fig.8 Simulation block diagramofoptimal control

搜索可得最优控制器的参数为Kp=0.589 95；Kd=0.201 69；Ku=1.122 9，仿真结果如图9。

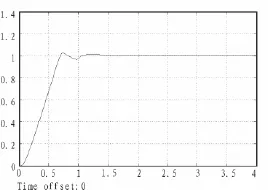
图9 遗传算法寻优仿真结果Fig.9 Simulation results of genetic algorithm optimization

与模糊控制器仿真结果相比，采用Kp=0.58995；Kd=0.20169；Ku=1.122 9的情况下，控制效果有显著改善。

4 结 论

本文采用模糊规则设计了二阶系统的模糊控制系统，在控制器不进行调整的情况下，系统动态响应超调较小、调节时间较短，控制效果较好。

本文采用遗传算法，按照ITAE准则对模糊控制器的参数进行优化，得到的参数更加合理，仿真结果几乎无超调，动态性能有显著改善。这反映出智能方法应用于控制系统中可以显著改善系统性能，控制器的参数优化具有重要的意义。本文较好的解决了欠阻尼二阶系统的控制问题。

[1]李士勇.模糊控制神经控制和智能控制论[M].哈尔滨：哈尔滨工业大学出版社，1996.

[2]李德毅.知识表示中的不确定性[J].中国工程科学，2000，2（10）:73-79.LIDe-yi.Uncertainty in knowledge representation[J].Engineering Science，2000，2（10）:73-79.

[3]李友善，李军.模糊控制理论及其在过程控制中的应用[M].北京:国防工业出版社，1992.

[4]张乃尧.用遗传算法优化模糊控制器的隶属度参数[J].电气自动化，1996，18（1）:4-6.ZHANG Nai-yao.Use genetic algorithem to optimize membership function parametersoffuzzy controller[J].Electrical Automation，1996，18（1）:4-6.

[5]刘琪，张鸿辉，黄贞贞.基于模糊C均值聚类方法的石油钻井工作状态分析[J].周口师范学院学报，2009（05）:53-55.LIU Qi，ZHANG Hong-hui，HUANG Zhen-zhen.Analysis of oil drilling working state based on fuzzy clustering method（FCM）[J].Journal of Zhoukou Normal University，2009（05）:53-55.

[6]刘琪，王少辉.分段线性隶属度函数确定的密度聚类方法[J].周口师范学院学报，2011（2）:57-58.LIU Qi，WANG Shao-hui.Piecewise-linearmembership function established by density clustering method[J].Journal of Zhoukou Normal University，2011（2）:57-58.