基于无证书的具有指定验证者的代理签名方案

梁景玲，高德智，张 云，葛荣亮

（山东科技大学 信息科学与工程学院,山东 青岛 266510）

在传统的公钥密码体制中，用户公钥的可靠性需要由一个可信任的第三方签署的证书来保证，但这不可避免的会存在密钥托管问题。为解决这一问题，在ASACRYPT2003上Al-Riyami和Paterson[1]提出了无证书公钥密码体制。在此体制中，用户的密钥由密钥生成中心使用主密钥为用户生成基于身份的部分签名和用户自选的秘密值两部分组成，用户则将上述两个部分联合起来独立生成私钥。因为用户独立生成私钥，KGC不知道用户真正的私钥，所以不存在基于身份的密钥托管问题。因此无认证公钥密码体制一经提出就受到了广泛关注，一些无证书签名方案也被陆续提出[2-3]。

而代理签名的概念是由Mambo等人[4]1996年首次提出的，当某个签名人因为某种原因（如健康、出差等）不能签名时，会将签名权利委托给他人行使。代理签名分为完全授权、部分授权和证书授权。并且代理签名应满足以下性质：可验证性、不可伪造性、可区分性不可否认性和放滥用性等。而在通常的代理签名中，代理签名的有效性可以由任何得到原始签名人和代理签名人公钥的人进行验证。然而当签名的消息是一些个人比较敏感的信息时，原始签名者只希望自己指定的验证者能够验证签名的有效性。为了解决这个问题，Jacobs等人[5]1996年首次提出了具有指定验证者的代理签名方案。在这种签名体制中，签名者会选择一个具体的验证者，仅有此验证者能够验证签名的有效性，这些体制在电子商务，电子政务中得到了很好的体现和应用。

然而，目前结合代理签名的无证书方案很少。文献[6]提出一个无证书代理签名方案，并宣称该方案不存在密钥托管问题，能够满足代理签名方案所要求的所有性质，且在效率上优于已有的基于身份的代理签名方案。而申军伟等人[7]随后指出，文献[6]虽然满足代理签名的所有性质，但此方案不满足可伪造性，不能抵抗替换公钥攻击和恶意的攻击，同时提出了一个改进的能够克服樊睿等人方案的新的方案。本文基于申君伟等人的改进方案，结合指定验证者提出了一个基于无证书的具有指定验证者的代理签名方案。该方案不存在密钥托管问题，并且能够抵制替换公钥攻击和密钥攻击，可以满足代理签名的一切性质，同时具有指定验证性，提高了安全性。

1 预备知识

1.1 双线性对

假设群G1和G2分别为阶为q的加法群和乘群，P为G1的生成元，假设群G1和G2中的离散对数均为困难问题，两个群之间的双线性映射e:G1×G1→G2满足如下特性：

1） 双线性性 对所有的 P，G∈G1和所有的 a，b∈Z*q：e（aP，bQ）=e（abP，Q）=e（P，abQ）=e（P，Q）ab。

2）非退化性 存在一个 P∈G1，满足 e（P，P）≠1。

3）可计算性 对 P，G∈G1，存在一个有效的算法计算 e（P，Q）。

对双线性映射可以利用椭圆曲线上的Weil对或Tate对来构造。

1.2 定义几个密码学问题

是可以忽略的。

3）判断性 Diffie-Hellman 难题（DDHP）：给定 P、aP、bP、cP∈G1，其中 a，b，c∈，要判定是否成立时困难的。

我们假设，在多项式时间内，以上问题都不可解。

假设G是一个加法群，在G上的4个数学难题分别是：

1）离散对数问题：设P和G是群中的两个元素，要找到某一个正整数n∈Z*q，使之满足Q=nP是困难的。

2）计算性 Diffie-Hellman 难题（CDHP）：对∀a，b∈Z*q给定 P、aP、bQ，计算 abP是困难的。

任何多项式时间内算法A能够成功解决CDH问题的可能性定义为：

2 申君伟等人的无证书代理签名方案

2.1 系统设置

G1和G2是阶均为q的循环加群和循环乘群，P∈G1作为G1的生成元，定义3个密码学上的单向哈希函数H1:{0，1}*×G1→G1，H2:{0，1}*×G2→，H3:G1→。 最后，KGC选择 s∈作为自己的私钥，计算公钥Ppub=sP，将s秘密保存，公开系统参数：params={G1，G2，e，q，P，Ppub，H1，H2，H3}。

2.2 密钥提取

原始签名人A随机选择秘密值xA，然后计算并公开公钥PA=xAP，KGC分别生成用户 A的部分私钥 DA=sQA=sH1（IDA，PA），并通过安全信道传给 A，A 秘密保存其私钥为（xA，DA）。通过相同的步骤生成代理签名者B的公钥PB以及私钥对（xB， DB）。

2.3 代理授权

A生成一个授权许可信息mw来说明包含A和B的身份信息的授权关系及其B的权限。A计算将（Sw，mw）发送给 B。B 验证等式 e（Sw，P）=e（QA，Ppub）·是否成立，若成立 B计算代理签名密钥

2.4 代理签名

当要对消息m签名时，代理签名人B选择a∈r，计算r=e （P，P）a，v=H2（mw， m，r），U=vSp+aP，则（U，v，mw）为 B 对 m 的代理签名。

2.5 验证

验证者首先计算 QA=H1（IDA，XA），QB=H1（IDB，XB），r=e（U，P）·[e（-QA-QB，Ppub）e（-H1（mw，XA），XA）e（-H1（mw，XB），XB）]v，然后验证等式 v=H2（mw，m，r），若成立则接受签名，否则拒绝。

3 新提出的方案

3.1 系统设置

G1为阶为q的循环加群，G2为循环乘群，阶亦是q。P∈G1作为 G1的生成元，定义3个单向哈希函数 H1:{0，1}*×G1→G1，H2:{0，1}*×G2→。最后，KGC 选择 s∈作为自己的私钥，计算公钥Ppub=sP，将s秘密保存，公开系统参数：params={G1，G2，e，q，P，Ppub，H1，H2，}。

3.2 密钥提取

原始签名人A随机选择秘密值xA，然后计算并公开公钥PA=xAP，KGC分别生成用户 A的部分私钥 DA=sQA=sH1（IDA，PA），并通过安全信道传给 A，A 秘密保存其私钥为（xA，DA）。代理签名者B和指定验证者C可以通过相同的步骤生成各自的公钥 PB，PC和私钥对（xB， DB），（xC， DC）。

3.3 代理密钥生成

A生成一个授权许可证书mw来说明包含A、B和C的身份信息及其B的代理权限、时间有效期等。A计算h1=H1（mw，xAPC），Sw=DA+xAh1，然后 A将（Sw，mw）秘密的发给 B。

B 在接收到（Sw，mw）后，首先验证等式 e（Sw，P）=e（QA，Ppub）e（h1，PA）是否成立。 若成立，B 则计算代理签名私钥 SP=Sw+DB+xBh1；若不成立，则拒绝授权。

3.4 代理签名生成

当要对消息m∈{0，1}*签名时，代理签名人B随机选择 a∈Z*q，然后计算 r=e（P，P）a，v=H2（mw，m，r），U=（vSP+aPC），则B把对信息m的签名（U，v，m）发送给指定验证者C。

3.5 验证

指定验证者C在接收到（U，v，m）签名后，首先计算QA=然后验证 v=H2（mw，m，r1）。 若成立，则接受签名；否则，拒绝签名。

4 安全性分析

4.1 正确性

指 定 验 证 者 首 先 计 算 ：H1（mw，xAPC）=H1（mw，xAxCP）=H1（mw，xAPC）=h1

若想验证 v=H2（mw，m，r）的正确性，即验证

因为：

所以：

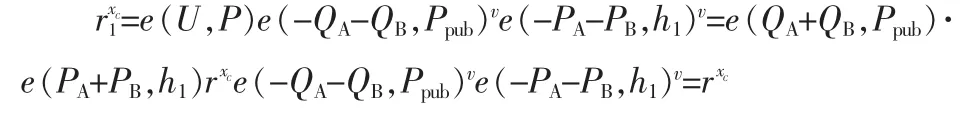
即验证等式 v=H2（mw，m，r）成立。

4.2 强不可伪造性

因为此方案是在申君伟等人方案的基础上得出的，所以此方案的授权过程在随机语言模型下可以抵御适应性选择消息攻击模式的存在性和ID攻击。又因为Sw=DA+xAh1是由原始签名者A使用KGC为其生成的部分私钥DA和自己自行选取的私钥 xA以及哈希值 h1=H1（mw，xAPC）产生的，除了原始签名人本身，就算是包括的任何攻击者都无法获得Sw的值。

另外，SP=Sw+DB+xBh1是由代理签名人B联合代理衍生密钥 Sw和 B本身的私钥对（xB，DB）产生的。 同样，DB是由 KGC为代理签名人产生的，而xA又是由B自己随机选取的。所以，就算KGC和原始签名人彼此勾结，他们也无法得到代理签名私钥Sp。

4.3 强不可否认性

首先原始签名人和指定验证者都不能对自己的授权和代理身份进行否认。因为，在完整的代理签名生成过程中一直在使用mw，代理签名人无法更改授权证书。而授权证书mw中包括原始签名人和代理签名人的身份信息，所以代理签名人一旦产生了合法的代理签名，就不能否认自己的签名，同时原始签名人也不能否认自己的授权身份。

另外，指定验证者也不能否认自己的指定验证身份。因为在签名阶段U=vSP+aPC的产生中，使用了指定验证者的公钥。所以，指定验证者C也无法否认自己的指定验证身份。

4.4 防止恶意的KGC攻击和公钥替换攻击

基于申君伟等人的方案，本方案中原始签名人、代理签名人和指定验证人先为自己选择了秘密值xA、xB和xC，计算出各自的公钥PA、PB和PC。然后将A、B和C各自的身份和公钥联合起来，嵌入KGC到为A、B和C生成的部分私钥里。而且本方案的部分私钥和秘密值是公开使用的。所以，这样可以有效的防止恶意的KGC攻击和公钥替换攻击。

4.5 指定验证性

5 结束语

本文结合指定验证者签名方案，在申君伟等人方案的基础上提出了基于无证书的具有指定验证者的代理签名方案[7]。经验证，该方案可以满足文献[7]提出的一切性质。同时，新提出的方案只有指定验证者能够对其签名方案进行验证，这保护了代理签名人的合法权益和隐私安全，在电子投票、网上招标以及软件许可等方面有极广泛的应用。此外，无证书公钥密码体制能有效解决基于证书密码体制的证书管理问题和基于身份密码体制的密钥托管问题。所以结合指定认证的无证书代理签名方案在某些电子商务中的应用前景及其广阔。

[1]Al-RiyamiS，PatersonK.Certificatelesspublickeycryptography[C]//Lecture Notes in Computer Science 2894:Advances in Cryptology Proceeding of Asiacrypt，2003:452-473.

[2]Du H，Wen Q.Efficient and provably-secure certificateless short signature scheme from bilinear pairings[J].Computer Standards&Interfaces，2009（31）：390-394.

[3]Harn L， Ren J， Lin C.Design of DL-based certificateless digital signature[J].The Journal of Systems and Software 2009（82）：789-793.

[4]MamboM，UsudaK，OkamotoE.Proxysignaturesfordelegating signing operation [C]//Proc of the 3rd ACM Conference on Computer and Communications Security，1996:48-57.

[5]Jacobson M，Sako K，Mpacli Azzo R，Designated verifier proofs and their applications:Proc of the EUROCRYPT&96[C].[s.1.]:Springer，1996:142-154.

[6]樊睿，王彩芬，蓝才会，等.新的无认证的代理签名方案[J].计算机工程，2008，28（4）：195-197.FAN Rui， WANG Cai-fen， LA Cai-hui，et al.A new certificatelessproxy signature[J].Computer Engineering，2008，28（4）：195-197.

[7]申君伟，杨晓元，梁中银，等.一种新的无证书代理签名方案的分析和改进[J].计算机工程与应用，2010，46（8）：96-98.SHEN Jun-wei， YANG Xiao-yuan， LIANG Zhong-yin， et al.Security analysis and improvement of new certificateless proxy signature[J].Computer Engineering and Applications，2010， 46（8）:96-98.