基于时间衰减和密度的任意簇数据流聚类*

龚 云，赵 鹏，王守军

（安徽大学 计算机科学与技术学院，安徽 合肥 230039）

数据流是指连续的、潜在无限量的、快速变化的、随时间而至的数据元素的流。由于数据采集的快捷化和自动化，数据库技术和互联网技术的飞速发展，日常生活已经与数据流息息相关，如网络实时监控、电子商务、卫星遥感等。这些数据都具有流的特性。而传统的数据挖掘方法需多遍扫描全部数据且数据必须以静态形式存储在磁盘空间里，因此用来专门处理数据流的数据处理模型和算法应运而生[1]。

CluStream算法是经典数据流聚类和主要算法，该算法提供了一个解决数据流聚类问题的优秀双层聚类方法，但由于它采用的是基于BIRCH算法的核心思想，所以仅限于得到球形聚簇结果[2]。K均值算法是基于划分的聚类方法，采用分而治之的策略对数据分块后再进行聚类，这样保证算法在较小的内存空间范围内获取常数因子的近似结果[3]。该算法的缺点是K取值的不确定因素太多，影响了准确性且不能考虑被分析数据的时间相关性。

1 基于时间衰减和簇合并的聚类处理算法（CluTA）

在分析某些类数据时往往更加注重其近期变化带来的影响，时间越久远被关注的程度就越低，如网络入侵行为的分类和趋势、股市不断变化的大盘信息等。为提高聚类得到结果的精确性，在挖掘时需考虑时间衰减的因素。由于K均值算法聚类的结果都是球型簇，本文通过合并相近相似簇达到输出任意形状簇的聚类结果。

本算法采用分层思想，第一层增加K均值算法得到中心点的信息，使每个中心点c中保留s(簇内所有的点到 c的距离和)、d(簇内最远点到 c的距离)、n(簇内所有点的个数)、t(c的生成时刻)。第二层结合本算法给出的衰减函数和密度计算出关键点的权重；比较关键点的权重和距离，如果距离足够近且权重比在允许范围内则合并簇。重复循环直到没有可合并的簇，输出最终结果。

1.1 相关定义和性质

假设数据以块X1,X2,…，Xn，…的形式按序到达，每个块内包含 m个数据点 xi（xi1,xi2,…，xim）且可以在内存中进行处理。每个数据点是一个d维向量。CluTA算法是以Kmeans为基础初次聚类生成k个关键点,采用五元组的方式存储关键点信息。

定义1.关键点

性质 1. 对任意关键点ri(ci，si，di，ni，ti)和数据点 p，均值点ci代表的所有数据点到p的距离和的上界为si＋ni×dist（ci，p）[4]。

性质 2. 对任意关键点 ri(ci，si，di，ni，ti)和 rj（cj，sj，dj，nj，tj)，设 c′为均值点 ci与 cj的中点,均值点 ci所代表的所有数据点到c′的距离和的上界可以有效替代其准确值[4]。

衰减函数表示簇随时间衰减的速率，当关键点生成时刻距当前时刻之差达到输入阈值△t后,即置权值为0，删除该关键点。

定义2.衰减函数Y=f(T)：

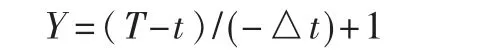
其中，△t为用户输入的有效时间范围阈值，t为该关键点的生成时刻，T为循环执行的当前时刻值，Y为衰减函数且取值在[0，1]之间的闭区间。

分析 T-t的取值范围，首先在 0＜T-t≤△t内讨论：当 T-t＜△t，Y>0表示此关键点是有效的； 当 T-t=△t，表示距离当前时间已达到用户设置的失效时长，此时Y=0,表示该关键点会被删除；若循环计算得T-t＞△t时，此时直接置Y=0。由此可见，T-t的值越大衰减函数Y的值越小，该关键点的实际使用价值越小。

定义3.可合并簇

任意两个相邻簇r1(c1，s1，d1，n1，t1)和 r2(c2，s2，d2，n2，t2)若满足下列条件，本文称为可合并簇。

(1)dist(c1，c2)≤d1+d2

上述(1)表示两簇的均值点距离小于或等于两簇内最远距离之和，相距足够近则考虑合并簇。但也可能出现两簇相距很近仍不符合合并要求的情况。如图1所示，两簇的距离足够近，但二者密度相差较大就不应该再合并。因此加上条件(2),通过计算两簇的权重比是否相差悬殊来决定是否可以合并。若上述限定条件都符合，则合并簇得到如图2所示结果。

1.2 CluTA算法

输入：△t为用户允许数据有效的时间范围;ε为用户允许两个可合并簇权重相差的比例，0＜ε＜1;r[][]为初始K均值聚类结束后得到的关键点。

输出：合并后簇的集合。

方法：

//处理初始K均值聚类结束后保留的关键点信息，进一步合并簇，精确聚类结果:

(1)取当前时刻记为T，计算任意关键点i，j间的距离

(2)repeat

//i，j两个簇的距离足够近且两个簇的权重比不超过设定范围，可以考虑合并:

(3)存储新生成点r′并置关键点 ci，cj为无效节点；

(4)until没有可合并的簇；

(5)输出聚簇结果。

1.3 算法分析

该算法改进K均值聚类算法结果信息，第一层运用K均值算法的计算复杂度为O(nkt)，n为数据点数目，t为循环次数，通常有 k＜＜n和 t＜＜n。第二层将生成的 k个聚簇进行合并，计算复杂度为O(k2)，k为常数级关键点数目。在K均值的基础上增加的内存空间也非常少，仅需保存k个关键点和一些中间变量。因此，该算法在时间和空间复杂度上都近似于K均值聚类算法，具有简单、高效的特点。

2 实验分析

算法在VC 6.0环境下采用C编写,实验平台为一台 CPU 2.8 GHz、内存 1 GB、操作系统为 Windows XP的PC机。采用了UCI的KDD CUP 1999网络入侵检测数据集。KDD CUP 1999数据集共23类，每一数据有42个属性，去除一些非数值型数据的维数，选留其中的20维做为实验数据。使用每类中的5 000条中的20个属性，打开文件模拟数据流环境读入数据,用Kmeans算法得出初始聚类关键点信息，再运用CluTA算法进行簇合并，最终与仅用Kmeans算法聚类的结果精确度比较，如图3所示，判断聚类质量的算法可参考文献[5]。聚类质量为类内距离值加上类间密度值。类内距离是表示该类内部点的密疏程度，类间密度是衡量各个类的平均密度关系，如图4所示，该值较小表明聚类簇集的类间区分度较好，因此二者总和越小，表示聚类质量越好。

为解决使用价值随时间衰减的一类流数据聚类问题和实现任意形状簇的聚类，本文在基于传统的K均值聚类算法基础上，保留其直观、高效的特点，提出了基于时间衰减的任意簇数据流聚类算法。即在K均值算法处理得到结果的基础上再考虑用时间和密度、空间距离等因素合并簇。理论分析和实验结果证明该算法相对于仅用K均值算法在处理对近期价值比较关心一类的数据时具有更精确的聚类结果。下一步的工作将着重于提高算法的效率和将其应用到更广泛的生活实践中。

[1]Han Jiawei.Micheline.Data Mining:Concepts and Techniques,Second Edition[M].China Machine Press,2008.

[2]AGGARWAL C C,et al.A framework for clustering evolving data streams.In:Proc.of the 29th VLDB Conf.,2003.

[3]GUHA S，MISHRA N，MOTWANI R.Clustering data streams[C].Proceedings of the Annual Symposium on Foundations of Computer Science.2000.

[4]倪巍伟，陆介平,陈耿，等.基于k均值分区的流数据高效密度聚类算法[J].小型微型计算机系统，2007，28(1):83-87.

[5]HALKIDI M,VAZIRGIANNIS M.Clustering validity assessment；finding the optimal partitioning of adata set[C].ICDM 2001:187-194.