一种改进的二叉树多分支持向量机算法*

周爱武,吴国进,崔丹丹

(安徽大学 计算机科学与技术学院,安徽 合肥230039)

支持向量机 (SVM)[1-2]是一种基于统计学理论的机器学习方法，由VAPNIK和CORTES于1995年首先提出。在解决小样本、非线性及高维向量空间的模式识别中具有良好的性能。支持向量机的思想是：如果是线性不可分，则通过某种非线性映射，将输入向量x映射到一高维特征空间Z，在这个空间中构造最优超平面，把不同的类分开；如果是线性可分，就可以直接构造最优超平面。但是传统的支持向量机分类方法是针对两类问题的二分方法，而实际应用中，更多的是多类问题，如何将一个两类分类方法扩展到多类的分类方法一直是人们研究的重点，目前SVM多类分类方法应用得较为广泛的有：“一对一”OVO(One-Versus-One)[3]、“一对多”OVR(One-Versus-Rest)[4]、“有向无环图”(DAG)[5]。 这些方法都是通过构造一系列的SVM二分器并将它们组合起来实现的多类分类。但是都存在不足之处，前两种方法存在线性不可分区域，第三种方法虽然解决了不可分区域问题，但各子类分类器在有向无环图中的位置会影响整个分类器的性能。所以人们又提出一种利用二叉树构造SVM的多类分类方法。

1 BT-SVM多类分类思想

BT-SVM的思想是：首先将所有类别分成两子类，再将子类进一步划分成两个次级子类，如此循环下去，直到所有的节点只包含一个单独的类别为止，这些节点也是二叉树的叶子节点，这样就得到了一棵二叉树。该方法将一个多类分类问题转化为一系列的两类分类问题，其中每个子类间的分类器都是SVM二值分类器，对于一个K类问题只需要构造K-1个分类器，这样相对于“一对一”、“一对多”及“有向无环图”方法构造所需的分类器都要少。另外，二叉树方法可以克服传统方法遇到的不可分问题。

二叉树结构的生成：例如，对于一个四类问题,可以有图1中的两种二叉树结构 (还有其他的结构没有列出)。对于不同的二叉树，会得到不同的分类模型，它们的推广性能也会不同。不同的层次结构对分类精度有一定影响，并且这种影响有可能产生“误差累积”现象，既若在某个节点上发生分类错误，将会把错误延续下去，该节点的后续下一级节点上的分类就失去了意义。越是上层节点的子分类器的分类性能对整个分类模型的推广性影响越大，因此，二叉树的结构生成问题是许多学者研究的重点。目前已经有大量此类论文研究分类相同的模型。

2 几种常用的二叉树生成算法

2.1 构造偏二叉树

由于上层节点的SVM子分类器的分类性能对整个分类模型的推广性影响最大，所以在二叉树的生成过程中，应该让与其他类别相差最大的类首先分割出来。此分类的基本思想是：利用聚类分析中的类距离作为二叉树的生成算法，让与其他类距离最远的类最先分割出来。图2为四类样本数据的二维空间分布图，所以应该先把与其他三类距离最远的第1类分割出来。在剩下的三个类中，第3类与其他两类的距离最远，所以再把第3类分割出来。剩下的第2类与第4类构造最后的二值分类器。这样就得到了一棵类似于图1(a)所示的二叉树。

定义类距离[6]：把类Sa与类Sb中两个最近样本向量之间的欧式距离作为两类之间的距离，即：

2.2 构造完全或近似完全二叉树

上面简单介绍了两种构造二叉树的方法，现在分析这两种方法的优缺点。第一种方法每次把与其他类距离之和最大的类分割出来，这样分类的准确性较高，但是，如果对于一个N类分类问题，其中有一个类别K，有可能在第一次就被分离出来，也有可能在第N-1次才被分离出来，这样分类的效率就会比较低，而且训练时间也比较慢。第二种方法，采用完全或近似完全二叉树，所以分类和训练的效率比较高，但是，在构造这颗二叉树时,每次都会把集合中的元素平均地分成两类，这是不现实的，因为，不能保证每个集合中的任一元素相对于所属集合的相似度大于另一个集合的相似度，这样分类的准确性就会较低。分类的准确性和分类的效率是一对矛盾，本文提出一种改进算法，既考虑分离的准确性，又能保证分类的效率。

3 改进的二叉树生成算法

3.1 相似度量函数

第2节定义的类距离，是将两类样本的最短距离作为两类的距离，这种方法虽然简单，但是没有考虑类样本的分布情况。本文采用球结构的距离计算方法[8]，该方法在定义类距离时既考虑了类中心又考虑了类的样本分布，是一种比较科学的方法。如图3所示的两类，它们的类中心距离相等，但是样本分布不同。图3(a)为两类相交，图 3(b)为两类相离。显然图3(a)比图 3(b)具有更高的相似性。因此，不能只以类中心的欧氏距离作为相似性度量函数，还需要考虑类样本的分布情况。球结构的SVM能构造出半径最小且尽可能包含该类所有样本的球体,因此球体的半径可以用来度量类样本的分布。

根据上述分析，可以用下面的距离计算公式作为类i与j间的相似性度量：

其中：ai，aj，Ri，Rj分别是第 i类和第 j类的中心和半径。 当dij≥0时，说明第i类与第j类没有相交区域。dij越大，说明第i类与第j类可分性越强，dij越小，说明两类的相似度越高。

3.2 改进算法

定义类平均距离：

其中：N为总类别数，dij为(2)式定义的类 i与类 j的距离，当 i=j时，定义 dij=0。 另定义集合 S、S1和 S2，Ns、Ns1、Ns2分别表示 S、S1、S2集合中类标号的个数。算法具体描述如下：

(1)对于一个N类问题，首先对N个类进行标号，标号为1,2,3…，N,并将这些类标号置入集合S中。由参考文献[9]中的式(10)和式(15)可得到每一类样本所在超球体的中心ai和半径 Ri(i=1,2,3,…,N)。根据式(2)和式(3)计算出 dij和 d。

(2)如果Ns=2，则把其中的一个类标号的类作为左子类，另一个类作为右子类，结束。

(3)计算集合S中的每一类到其他类的距离dij，统计每个类到其他类距离小于λd类的个数 (λ是一个大于零的参数，对于不同的样本分布情况，通过调整λ值来提高分类的精度)，记作：Numi(i=1,2,3,…,N)。例如第 i类，统计这个类到其他N-1个类的距离小于λd的类个数，计入Numi。找出最大的Numi(如果存在不唯一，任意选择其中一个)，如果 Numi=Ns，则转入(4)，否则，将标号i 置入集合 S1，并将满足 dij＜λd(j=1,2,3,…,Ns,j≠i)的类的标号置入S1，将 S剩下的类的标号置入S2。S1中类标号对应的类就作为二叉树的左之类，S2中类标号对应的类作为二叉树的右子类。转到(5)。

(4)如果出现这种情况，说明类之间的相似度比较高，可以根据参考文献[11]中提出的二叉树生产算法，构造一颗完全或近似完全二叉树。结束。

(5)经过步骤(3)，集合S1中的类别相似度比较高，可以根据参考文献[11]中提出的二叉树生产算法，以集合S1对应的左子类作为顶层节点构造一颗完全或近似完全二叉树。

(6)如果 Ns2=1，则结束。否则将集合 S2中的类别号置入S，将得到的右子类作为顶层节点，回到步骤(2)。

经过上面的步骤，可以构造出一棵二叉树，这个二叉树可能是一个偏二叉树，也可能是一个完全二叉树，但是这两种都是极端的情况。更多的情况下构造的二叉树总体上是一棵偏二叉树，局部是一棵完全或近似完全二叉树。这样做的好处是，既保证了分类的准确性，又保证了分类的速度。

4 实验分析

下面以N=9的情况分析本文提出的算法构造的二叉树，并与参考文献[11]中构造的完全二叉树做比较。图4是9类样本的球结构在二维空间分布情况，图5是球心坐标,图6是根据式(2)计算出的各类间的距离。由图6中的数据可以计算出d=2.966，λ取0.5。根据本文提出的算法，构造出图 7(a)所示的二叉树，图 7(b)图是根据参考文献[11]算法构造的二叉树(构造的偏二叉树在这里没有画出)。

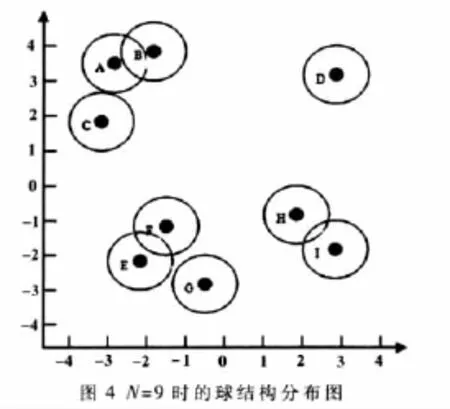
从图4的样本分布图可以看出，图 7(a)所示的二叉树分类更符合样本的分布情况。而图7(b)所示的二叉树把原本相似度非常高的 E、F、G三个类拆分成了 EF和 G，这显然是不合理的，出现这种情况的原因是因为此算法要求构造一个完全二叉树，左子树和右子树包含的类别个数只能相差0或1，所以有些相似度高的类就被拆分开了。这样就会产生分类误差，而且本实验在一开始就出现这种误差会影响后面的分类结果，出现误差累积的现象。而本文提出的算法，首先把相似度高的ABC先分割出来，再把EFG分割出来，最后把HI和D分开，这样的结果符合样本的真实分布，所以具有比较高的分类精度。

再把图7(a)构造的二叉树与偏二叉树作一下比较，偏二叉树每次只有一个类被分离出来，所以训练速度比较慢，而且在后面分类时效率也比较低。而本文构造的二叉树每次会把相似度比较高的一些类先分出来，再将这些类构造一个完全或近似完全二叉树，所以训练的时间会比偏二叉树低而分类的速度要更快。

本文结合偏二叉树和完全二叉树的构造思想，提出了一种基于球结构的二叉树生产算法，利用该算法构造出的二叉树更接近样本的真实分布，具有较高的分类精度和分类速度。但是算法还存在一些没有解决的问题，例如：在算法中要求 dij＜λd，本文参数λ取 0.5，对于其他样本λ值可能会取不同的值，所以λ的取值问题是今后研究的重点。

[1]VAPNIK V.Statistical learning theory[M].New York:Wiley,1988.

[2]邓乃扬，田英杰.支持向量机.北京：科学出版社，2009.

[3]BOTTOU L,CORTES,DENKER J.Comparison of classifier Methods:a case study in handwriting digit recognition[C]//Proceedings of the 12th IAPR International Conferenceon Pattern Recognition,Jerusalerm:IEEE,1994.

[4]KREBERL U.Pair wise classification and support vector machines[C]//Advances In Kernel Methods-Support Vector Learnning,Cambrige:MIT Press,1999:255-268.

[5]PLATT J C,CRISTIANINI N,SHAWE～TAY-LOR J.Large Margin DAGs for multiclass classification[C]//Advances in Neural Information Processing systems,Cambridge:Mtt Press,2000:547-268.

[6]唐发明，王仲东，陈绵云.一种新的二叉树多类支持向量机算法[J].计算机工程与应用,2005,41(7):24-26.

[7]张贝贝，何中市.基于支持向量机数据描述算法的SVM多分类别新方法[J].计算机应用研究,2007,24(11):46-48.

[8]唐发明，王仲东，陈绵云.支持向量机多类分类算法研究[J].控制与决策,2005,20(7):746-749.

[9]Hao Peiyi,LIN Y H.A new multi-class support vector machine with multi-sphere in the feature Space[C].Lecture Notes in Computer Science.BerLin,Heidelberg:Springer-Verlag,2007:756-765.

[10]张晓平,杨洁明.一种新的支持向量机多类分类二叉树生成算法[J].机械工程与自动化,2007(3):1-3.

[11]谢志强,高丽,杨静.基于球结构的完全二叉树SVM多类分类算法[J].计算机应用研究,2008，25(11):3268-3274.