Dy(Co1-xMnx)2合金的相变和磁热效应

韩志达 ，陈 杰

（常熟理工学院 a.物理与电子工程学院，b.江苏省新型功能材料重点建设实验室，江苏 常熟 215500）

磁制冷是利用自旋系统磁熵变的制冷方式，是以磁性材料为工质的独特的制冷技术.由于磁制冷技术具有高效、环保、稳定等优点，具有巨大的市场潜力，成为凝聚态物理、材料、能源、环保等领域活跃的研究方向.低温磁制冷早已实现应用[1]，目前室温磁制冷是磁制冷技术中的研究热点.发展室温磁制冷技术的一个重要任务就是寻找室温附近具有巨大的磁热效应的廉价的磁制冷材料[1].在众多磁致冷材料中，稀土基磁致冷材料（如 Gd[2]，Gd-Si-Ge[3]，RCo2（R=Dy，Co，Er）[4-6]，Gd基非晶[7]等）由于具有较大磁矩成为理想的磁致冷材料.

RCo2（R为稀土金属或Y和Sc）作为其中一种代表性的金属间化合物[8].它们的性质介于RNi2和RFe2之间：前者表现顺磁性，后者表现稳定的铁磁性.当RCo2中R为非磁性的Y或Lu，材料表现为泡利顺磁性，加磁场时则出现了变磁性相变——即当外场大于某个临界场时，Co将被诱导产生磁矩，从而有一个由外场导致的从顺磁态到铁磁态的磁性相变[9].当R为磁性金属离子，3d（Co）与4f（R）之间的交换作用场有可能大于相变临界场，从而诱导出Co的磁矩（大约为1μB左右），产生变磁性相变.当R为Dy、Co、Er时，磁性相变类型为一级相变，伴随着巨大磁化强度的突变，因而具有较大的磁热效应.王敦辉等人研究了Si、Al替代Co对DyCo2的相变和磁热效应的影响，发现少量掺杂能在保持一级相变的同时，提高居里温度，从而在较宽的温区内获得了巨大的低熵磁熵变[10，11].本文研究了Mn替代Co对DyCo2磁性、相变和磁热效应的影响，拓宽了其作为磁制冷材料的工作温区.

1 实 验

使用的原材料Dy、Co、Mn的纯度均在99.9%以上，按化学配比Dy（Co1-xMnx）2（x=0，0.02，0.04，0.06，0.08，0.1）将原材料放进电弧炉中，在氩气保护下反复翻转熔炼3次.然后将样品密封在石英管内在950℃退火7天，最后使其在冷水中快淬.样品的结构用X射线衍射仪（XRD）测量，样品的磁学性质用Lakeshore7300振动样品磁强计（VSM）测量，样品在10kOe外场下的磁熵变（SM通过Maxwell关系式进行计算.

2 结果与讨论

图1列出了Dy（Co1-xMnx）2合金的XRD图谱.从图中可以看出，所有样品结构与DyCo2相同，均为MgCu2类型Laves相结构，未观察到明显的1：3相.根据XRD结果，我们计算了Dy（Co1-xMnx）2合金的晶格常数（如表1所示）.随着Mn含量的增加，a逐步变大，这说明了原子半径较大的Mn原子确实替代了Co.

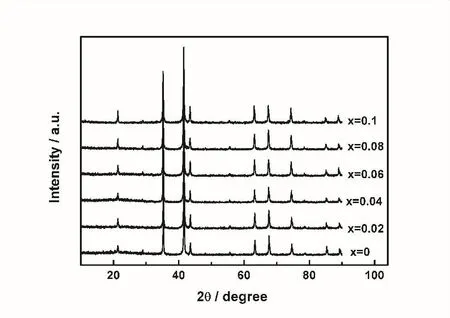
图1 Dy(Co1-xMnx)2合金的XRD

表1 Dy(Co1-xMnx)2的晶格常数a、居里温度Tc、10kOe下的磁熵变|△SM|

图2为Dy（Co1-xMnx）2合金在1kOe磁场下的升温热磁曲线.从图中可以发现，随着Mn掺杂量的增加，样品的居里温度随之升高，同时磁化强度随温度的变化趋势也逐渐由陡峭变为平缓.这种现象揭示了相变类型从一级到二级的转变.但仅仅从热磁曲线的实验结果很难确定一个陡峭与平缓的界限，即一级相变与二级相变的分界点，虽然很多前人的工作中都以磁化强度、电阻、晶格常数等随温度变化的快慢（即曲线陡峭与否）来判断相变的类型.实际上，这和实验中取点的密度，延迟时间的长短等都有关系[8].

在DyCo2、ErCo2和HoCo2的相变温度加磁场时，将可能诱导产生一级相变，表现在等温磁化曲线中磁化强度有明显的跳跃现象[4，5].这些都与Co的变磁性转变的产生有关.由于实验条件限制，样品的等温磁化曲线都是在10kOe的外场下进行的.如图3和图4所示，我们发现在10kOe这样相对较低的磁场下所测量到的曲线中，我们几乎观察不到因相变类型的不同而导致的磁化曲线的差别.这样看来从低场等温磁化曲线中也很难判断相变类型.

图2 Dy(Co1-xMnx)2合金在1kOe磁场下的热磁曲线

为了判断相变的类型，我们采用了Inoue-Shimizu模型[12].这个模型中采用了s-d模型来描述局域磁矩和巡游电子之间的相互作用.其自由能可以展开成磁化强度M的函数：

图3 DyCo2在居里温度附近的等温磁化曲线

图4 Dy(Co0.98Mn0.02)2在居里温度附近的等温磁化曲线

在这里相变的类型可以通过C3（Tc）的符号来判断[13]：如果C3（Tc）＜0，那么相变类型为一级相变，否则就是二级相变.而C3（Tc）的符号可以通过Arrott曲线来判断.通过画M2-H/M曲线，我们就可以得到Arrott曲线.在一级相变材料中，当变磁性相变出现时，居里温度附近Arrott曲线呈现负的斜率或者表现出S形状，此时c3（T）为负值，否则为正[14].

图5和图6分别是DyCo2和Dy（Co0.98Mn0.02）2的Arrott曲线.由图5可以看出，在Tc附近，Arrott曲线呈现S形，这说明对于DyCo2来说，c3（TC）为负值，因而相变类型为一级相变.由图6，在居里温度附近没有观察到明显的S形状，说明这些样品中没有变磁性相变的出现，因而可以判断其相变为二级相变.

图5 DyCo2的Arrott曲线

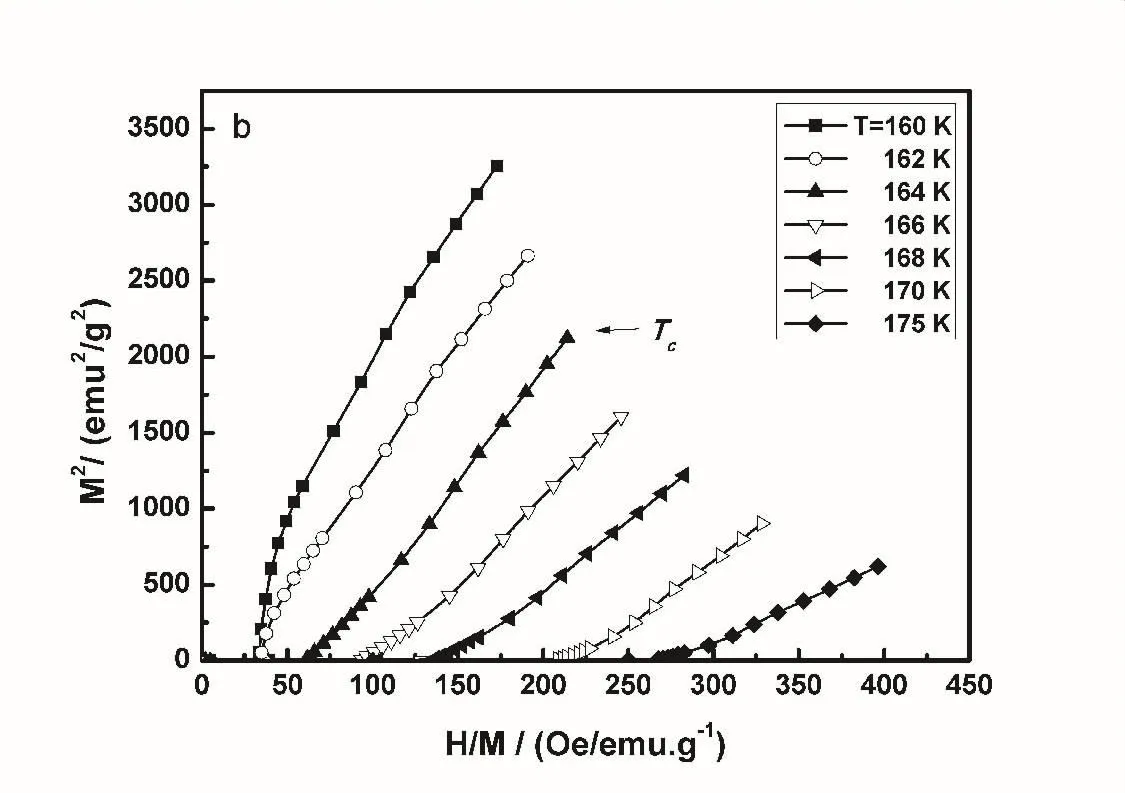
图6 Dy(Co0.98Mn0.02)2的Arrot曲线

我们利用Maxwell关系和磁性测量的数据，分别计算了各个样品在10kOe外场下的磁熵变值.图7是Dy（Co1-xMnx）2合金的磁熵变随温度的变化关系图（|（△SM|-T）.从图中我们可以看出，样品的磁熵变都在居里温度附近达到最大值.随着掺杂量的增加，样品的磁熵变也随之逐步减小，可以看出因一级相变导致的磁熵变明显大于二级相变导致的磁熵变.这是由于一级相变的材料磁化强度能够在很窄的温度范围内迅速降低，从式（1）可以看出，∂M/∂T越大，所产生的磁熵变也越大.虽然Mn的掺入导致了磁熵变的减小，但同时也使磁熵变的峰展宽，这对于磁制冷材料是有利的.

图7 Dy(Co1-xMnx)2合金在10kOe磁场下的磁熵变

3 结 论

1.在Dy（Co1-xMnx）2中，Mn替代Co不改变晶体的结构，仅使晶格常数增加，同时居里温度大大增加.当x从0变到0.1时，居里温度从142K增加到220K.

2.通过Arrott曲线分析表明，Mn掺杂使相变类型从一级相变变为二级相变.由于相变类型的变化，磁熵变大小随Mn含量增加逐渐减小，同时磁熵变的峰有所变宽.

3.Dy（Co1-xMnx）2合金以其低成本、大磁熵变、可调的工作温区，成为一类具有巨大应用潜力的磁制冷材料.

[1]Brück E.Developments in magnetocaloric refrigeration[J].JPhysD,2005,38(23)：R381-R402.

[2]Gschneidner Jr K A, Pecharsky V K.Rare earths and magnetic refrigeration [J].J Rare Earths, 2006, 24(6)： 641-664.

[3]Pecharsky V K, Gschneidner K A.Giant magnetocaloric effect in Gd5(Si2Ge2)[J].Phys Rev Lett,1997,78(23)：4494-4497.

[4]Oliveira N A de, Ranke P J Von, Costa M V Tovar, et al.Magnetocaloric effect in the intermetallic compounds RCo2(R=Dy, Ho, Er)[J].Phys Rev B, 2002, 66： 094402-094407.

[5]Duc NH,Kim Anh DT.Magnetocaloric effects in RCo2compounds[J].JMagn Magn Mater,2002,873：242-245.

[6]Wada H, Tomekawa S, Shiga M.Magnetocaloric properties of a first-order magnetic transition system ErCo2[J].Cryogenics,1999,39(11)：915-917.

[7]Luo Q, Zhao D Q, Pan M X, et al.Magnetocaloric effect in Gd-based bulk metallic glasses [J].Appl Phys Lett, 2006, 89(8)：081914-081916.

[8]Duc NH,Brommer PE.Handbook on Mangneitc Materials[M].Amsterdam：Elsevier,1999：250-394.

[9]Goto T, Sakakibara T, Mutara K, et al.Itinerant electron metamagnetism in YCo2and LuCo2[J].JMagn Magn Mater,1990,90-91：700-702.

[10]Wang D H,Liu H D,Tang S L,et al.Low-field magnetic entropy change in Dy(Co1-xSix)2[J].Solid State Comm,2002,121(4)：199-202.

[11]Liu H D,Wang DH,Tang SL,etal.The magnetocaloric effect and magnetic phase transitions in Dy(Co1-xAlx)2compounds[J].JAl-loys Comp,2002,346(1-2)：314-319.

[12]Inoue J,Shimizu M.Volume dependence of the 1st-order transition-temperature for RCo2compounds[J].JPhys F,1982,12(8)：1811-1819.

[13]Duc NH,Brommer PE,Franse JJM.Magnetic phase-transitions in(Nd,Dy)Co2and(Pr,Dy)Co2compounds[J].Physica B,1993,191(3-4)：239-247.

[14]Duc N H,Anh D T K,Brommer PE.Metamagnetism,giant magnetoresistance and magnetocaloric effects in RCo2-based com-pounds in the vicinity of the Curie temperature[J].Physica B,2002,319(1-4)：1-8.