一类Weierstrass型函数的分数阶W-M导数图象的分形维数
2011-05-15李红娟
李红娟
(太原理工大学 理学院,太原 030024)
自微积分诞生之日起人们就提出了分数阶形式的微积分问题,只是没有引起人们的重视,直到非线性问题的研究与分形几何的出现才使得分数阶微积分再一次回到人们的视野,分数阶微积分与分形、特别是分形函数紧密相连,它为处理处处连续但处处不可微的分形函数及其图像提供了一种可行的工具。
分数阶微积分最早有系统化的研究是由 Liouville(1832年),Riemann(1853年)和Holmgren(1864年)在19世纪初期和中叶完成的,但Grunwald和Krug最先统一了Liouville和Riemann分数阶微积分定义。针对分数阶微积分,人们又提出许多不同的定义,例如Grunwald分数阶微积分,Weyl-Marchaud分数阶微积分,局部分数阶微分,Caputo分数阶微分等等。分数阶微积分是研究分形函数的有力工具,B.B.Mandelbrot,F.B.Tatom,M.Zahle,K.M.Kolwankar,W.Y.Su等在这方面作了许多有益的工作。
近年来人们将分形函数与分数阶微积分的理论相结合,求出了一些分形函数的分数阶微积分函数,并对其图像和分形维数进行了讨论。姚奎、苏维宜、周颂平等人针对分形函数中的一类典型函数Weierstrass函数的分数阶微积分函数的图像的分形性质和分形维数进行了较全面的研究,应用Riemann-Liouville的分数阶微积分的定义得出了这类函数的分数阶微积分函数,对函数图像的分形维数进行了系统的研究[1-4]。另外他们将Weierstrass函数扩展成更一般的Besicovitch函数,并对此函数的一些相应性质和结论进行了进一步的探讨。本文在前人对Weierstrass函数的分数阶微积分及其维数的研究基础上,引入一类更一般的Weierstrass型函数,应用Weyl-Marchaud分数阶导数的定义求出了类分形函数的分数阶导函数图像的维数。
1 主要定义

定义1 Weierstrass型函数
分别称为f的ν阶Weyl-Marchaud左、右导数。如果 Dνl f(x)=Dνrf(x),我们称 f(x)的 ν阶 Weyl-Marchaud可导,记为 Dνf。
定义3 记:

表示ψ(ax)的ν阶W-M 导数。记:

是W(t)的ν阶分数阶W-M 导数。
定义4 设 ψ:[0,1]→R为连续函数,记函数ψ(t)在区间Ι上的振幅为

记函数ψ(t)的图像为

2 主要定理的证明
定理1 设0<ν<α<1,ψ∈ A,那么
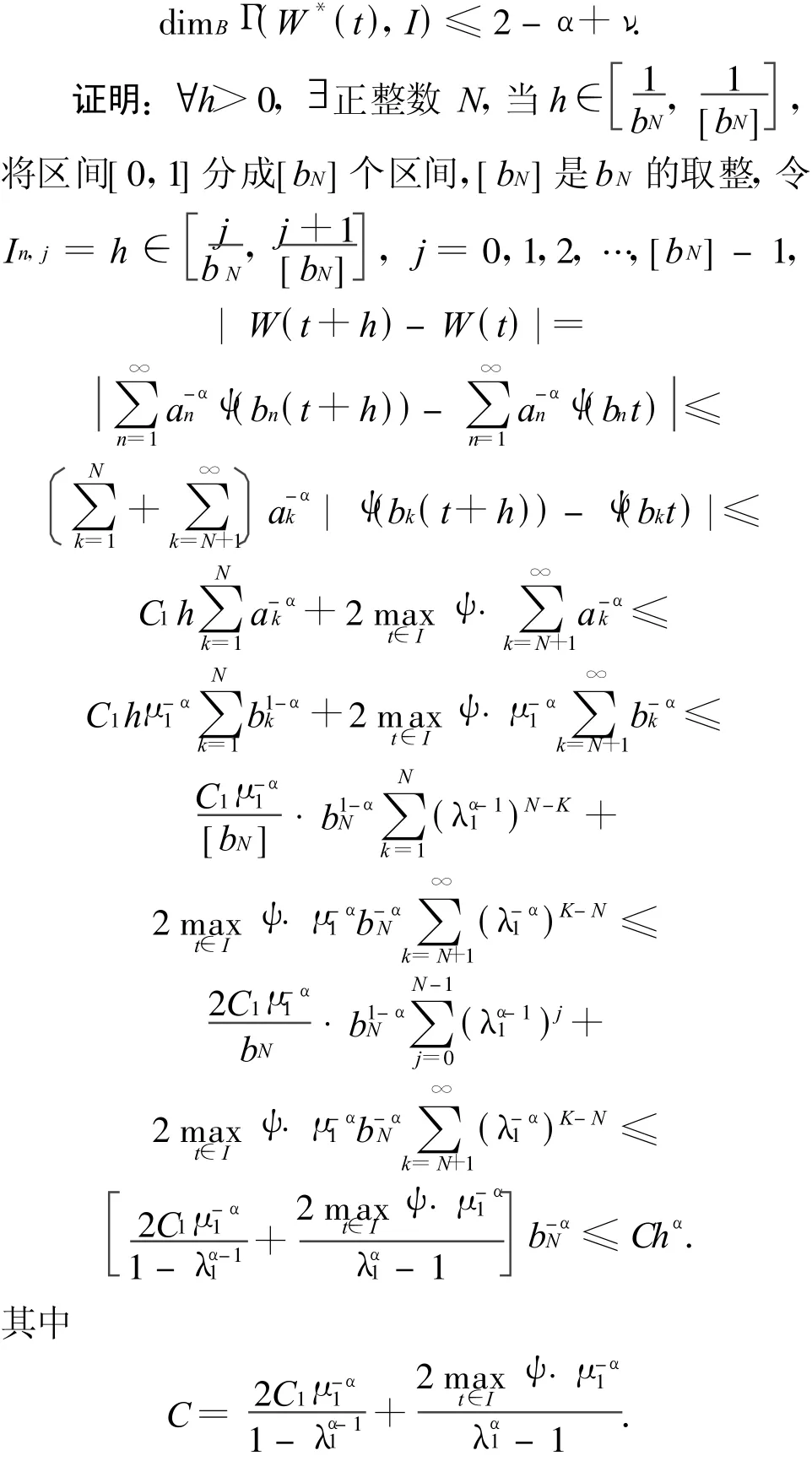
所以
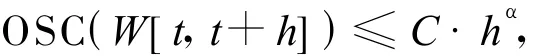
由文献[5]可得出:
dim BΓ(W,I)=dim KΓ(W,I) ≤2- α.
那么
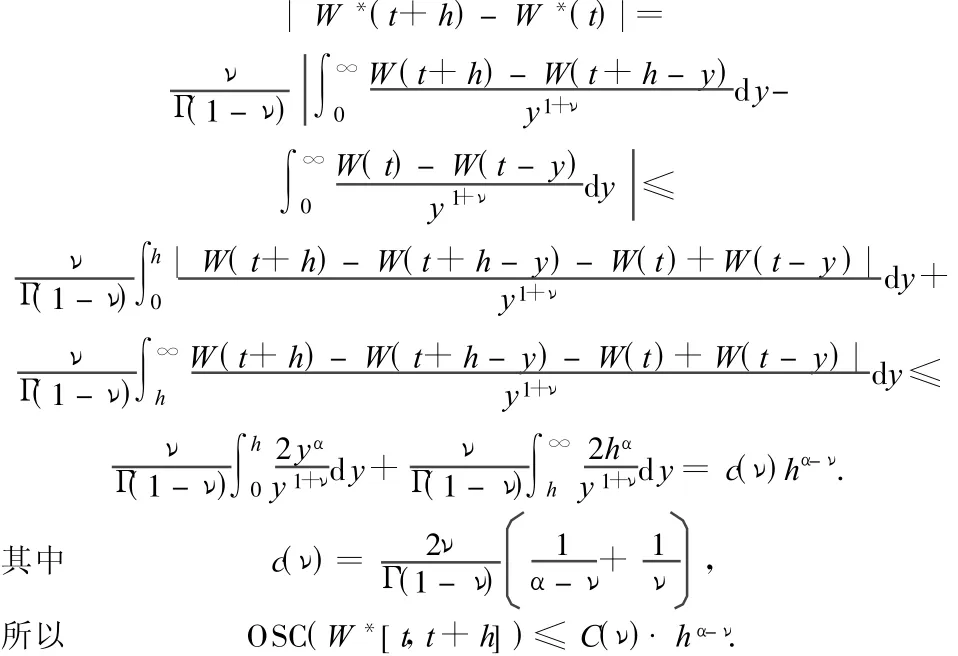
由文献[5]可得出:
dim BΓ(W*,I)=dim KΓ(W*,I) ≤2- α+v.
引理1 设 ψ∈A,0<ν<1,则

而C*是一定正常数。
证明:



定理2 设I=[0,1],ψ∈A,0<ν<α<1并且u=min(1- α,α- ν),

注意到λ1>3,则至少存在一点 ti和δi,使得 ti∈A,(ti,ti+h)⊂δi,由引理1的3)得:

所以 OSC(W*,δi) ≥C(ν)bν-αN.
由文献[5]可得出:
dim BΓ(W*,I)=dim KΓ(W*,I) ≥2- α+ν.
由上可知,设
0<ν<α<1,ψ∈ A,
则
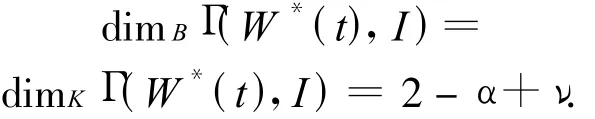
[1] 姚奎.分形函数与分数阶微积分:构造性方法的应用[D].杭州:浙江大学,2003.
[2] 姚奎,苏维宜,周颂平.关于一类Weier strass函数的分数阶微积分函数[J].数学年刊,2004,25A(6):711-716.
[3] Zahle M,Ziezold H.Fractional derivatives of Weierstrass-type functions[J].Computa-tional and Applied Mathematics,1996,76:265-275,265-273.
[4] Yao K,Su W Y,Zhou S P.On the fractional calculus functions of a fractal function[J].Appl Math J Chinese Univ Ser B,2002,17(4):377-381.
[5] Falconer J.Fractal geometry :Mathematical foundations and Applications[M].New York:John Wiley Sons Inc,1990.
[6] 华宇明.Weierstrass型函数图像的分形函数[J].应用数学与计算数学学报,1994,8(1):78-85.
