二阶差分方程边值问题解的存在性

张福伟,刘进生

(太原理工大学 理学院,太原 030024)

1 引言及主要结果

解的存在性。其中 T≥3是一个固定的整数,k∈[1,T]=1,2,…,T ,常数 α＜1,β≤1,非线性项f：[1,T]×R1→R1关于第二个变量连续。Δ是向前差分算子,即 Δuk-1=uk-uk-1,而 Δ2uk-1=ΔΔuk-1。

由于计算机技术的高速发展,使得各种模型的数值求解成为可能,因而系统的离散化——差分方程的应用领域更加广泛。故近年来有许多作者利用变分方法,结合临界点理论研究问题(1)解的存在性,例如文[1-6]及其参考文献等。作者们应用临界点理论中的强单调映像原理、山路引理、弱下半连续性与强制性、偶泛函临界点定理以及一些其他的临界点知识,在各种相应的假设条件下证明了问题(1)单个解与多个解的存在性。本文的假设条件与上述文献等不同,我们注意到问题(1)解空间的维数有限,从而仅利用一个有限维空间上泛函临界点的存在性结论及鞍点定理,只用一个非常简单的假设条件,即可保证问题(1)至少存在一个解。记

本文研究非线性二阶差分方程两点边值问题

共有 T个特征值,并且满足条件λT≥λT-1≥…≥λ1＞0.令我们研究当Fk≠λj/2时,问题(1)解的存在性,主要结果如下。

定理 1 如果Fk＜λ1/2或者Fk＞λT/2,则问题(1)至少存在一个解。

由于对满足条件的任意常数 α,β,λ1及 λT不易求出,为方便定理1假设条件的验证,我们给出如下一些直观推论。

推论1 如果Fk=-∞或者Fk=+∞,则问题(1)至少存在一个解。

推论2 如果F k≤0或者 Fk≥T-(α+β)/2,则问题(1)至少存在一个解。

推论3 如果下列条件之一满足,则问题(1)至少存在一个解：

则又可以得到下列推论。

推论4 如果 f k＜λ1或者 f k＞λT,则问题(1)至少存在一个解。

推论5 如果f k=-∞或者 f k=+∞,则问题(1)至少存在一个解。

推论6 如果 f k≤0或者 f k≥2T-(α+β),则问题(1)至少存在一个解。

推论7 如果下列条件之一满足,则问题(1)至少存在一个解：

当 Fk∈(λj/2,λj+1/2)时,相应的结论需要进一步研究,但本文得到了下列结果。

定理2 假设 fk=a并且存在某个j∈[1,T-1]使得λj＜a＜λj+1,则问题(1)至少存在一个解。

推论8 假设 f k=a并且存在某个j∈[1,T-1]使得

则问题(1)至少存在一个解。

注1 定理1至定理2及推论1至推论8中涉及到变量k的等式或者不等式均表示对k∈[1,T]一致成立。

2 主要结果的证明

定理1的证明 分别令

容易知道问题(1)等价于非线性方程组

假设Fk＜λ1/2,下面首先证明

由假设条件知

再由(9)知,对任意的 M＞0,存在tM＞0,当 t ＞tM时,

因此(8)成立。而

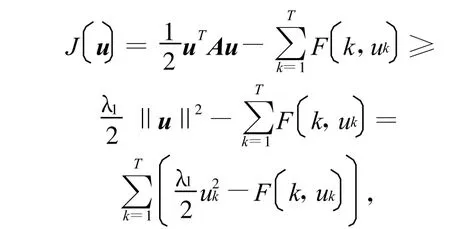
推论1-7的证明 除推论3及7之外,其余推论显然成立,下面给出推论3(从而由推论3可得到推论7)的证明。记

那么A=B+Q,而B的特征值λk(B)=

所以推论3及推论7成立。

定理2的证明 改写泛函I为T阶单位矩阵。那么

注意到

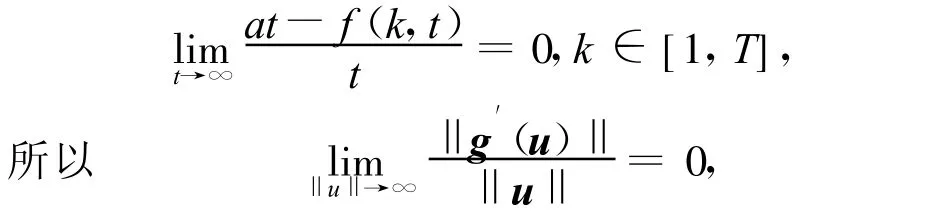
而 f：[1,T]×R1→R1关于第二个变量连续,空间H维数有限,所以 g′：H →H 是紧算子。又因为 λj＜a＜λj+1,于是矩阵A-a I可逆。因此,根据文[7]的引理5.1及注5.2知泛函J在H中满足P.S.条件。

而当u∈V⊥j并且‖u‖→∞时,

从而由文[9]的鞍点定理知泛函J在H中至少存在一个临界点,所以问题(1)至少存在一个解。

利用定理2,结合(11)式,即可得到推论8。

注2 当Fk=λj/2(此时称问题(1)共振)时,需要增加其它的假设条件才能确保问题(1)解的存在性,其研究较为复杂,我们将另行考虑,类似的结果也可见文[10]。

[1] Jiang Liqun,Zhou Zhan.Existence of nontrivial solutions for discrete nonlinear two point boundary value p roblems[J].Applied Mathematics and Computation,2006,180：318-329.

[2] Bai Dingyong,Xu Yuangtong.Nontrivial solutionsof boundary value problems of second-order difference equations[J].J Math Anal Appl,2007,326：297-302.

[3] Yang Yang,Zhang Jihui.Existence results for a nonlinear system with a parameter[J].J Math Anal Appl,2008,340：658-668.

[4] Jiang Liqun,Zhan Zhou.Multiple nontrivial solutions for a class of higher dimensional discrete boundary value p roblems[J].App lied Mathematics and Computation,2008,203：30-38.

[5] Yang Yang,Zhang Jihui.Existence and multiple solutions for a nonlinear system with a parameter[J].Nonlinear Analysis,2009,70：2542-2548.

[6] Yang Yang,Zhang Jihui.Existence of solutions for some discrete boundary value problems with a parameter[J].Applied M athematics and Computation,2009,211：293-302.

[7] 张恭庆,临界点理论及其应用[M].上海：上海科学技术出版社,1986.

[8] 程云鹏,矩阵论[M].西安：西北工业大学出版社,1989.

[9] Rabinowitz P H.Some Minimax Theorems and Applicationsto Nonlinear Partial Differential Equations：A Collection of Papers in Honor of Erich N Rothe[M].Academic Press,1978：161-177.

[10] Liu Jinsheng,Wang Shuli,Zhang Jianming.M ultiple solutions for boundary value problems of second-order difference equations with resonance[J].J Math Anal App l,2011,374：187-196.