基于IQRD-RLS的自适应均衡算法在DS-SS系统的应用研究

李 明，黄 华，夏建刚

(四川大学 电气信息学院，四川 成都 610065)

在目前的移动通信领域中，克服多径干扰、降低出错率，是提高通信质量一个非常重要的问题。特别是当信道特性不固定时，该问题尤为突出，而自适应滤波器[1]，则完美地解决了这一问题。自适应滤波器的核心就是自适应算法，而自适应算法有很多，如LMS算法、归一化NLMS算法和RLS算法等，这些算法已经广泛应用于通信、系统辨识、信号处理和自适应控制等领域。但是这些算法是在有限精度运算条件下，舍入误差的积累，容易导致算法的不稳定。在实际应用中，需要一个具有略高的运算复杂度且数值稳定性良好的自适应滤波算法。因为一个数值鲁棒性好的自适应滤波算法可以用更短的字长甚至定点运算实现，同时又可以减少时延。

本文基于逆QR分解[2]提出了一种更有效逆QR分解的RLS自适应算法 (IQRD-RLS)，它能有效降低计算复杂度、改善矩阵条件数，具有比基于相关矩阵的最小二乘算法有更好的数值稳定性。该算法的主要优点是可以采用脉动阵[3]，并在考虑量化效应时改善算法的数值特性。逆QR分解方法避免了RLS问题的不准确求解问题，并且很容易随时检查变换信息矩阵的正定性。通过在(DS-SS)扩频系统[4]进行仿真，验证了逆IQRD-RLS算法所具有的特性，起到了减少信道传输错误、滤除干扰的效果，改善了滤波性能，因而值得继续深入研究其他基于IQRD-RLS算法的改进算法。

1 基于逆QR分解的RLS算法

数据矩阵的QR分解是：如果复(实)矩阵A可以分解成一个酉(正交)矩阵Q和一个复(实)的上三角矩阵R的乘积，即A=QR，则称该式为A的一个QR分解。由此可以得到一个长方矩阵的分解定理：设n×r矩阵A∈Cn×r(∈Rn×r)且 rankA=r，则存在 n 阶酉(正交)矩阵和 r阶与复(实)的正线上三角矩阵 R，使得：

当n=r时，长方矩阵就变成正方矩阵，同样QR分解定理存在。

基于逆QR分解[5]的递推最小二乘算法，首先采用Givens旋转等正交变换把加权输入信号矩阵变换为上三角矩阵，然后再利用回代法求解三角矩阵方程，计算自适应滤波器的权系数向量。与标准的递推最小二乘算法一样，基于逆QR分解的递推最小二乘算法也是基于最小二乘准则，即：求解权系数向量 w(k)，使估计误差的指数加权平方和最小。假设x(k)为输入信号、y(k)为期望输出信号、N为滤波器阶数，则IQRD-RLS算法中的代价函数可以表示为：

式中，λ是遗忘因子，0<λ≤1。代价函数也可以表示为矩阵形式。定义k×k对角矩阵∧(k)如下：

k×1维加权期望输出信号向量 y(k)和 k×N维加权输入信号矩阵X(k)定义如下：

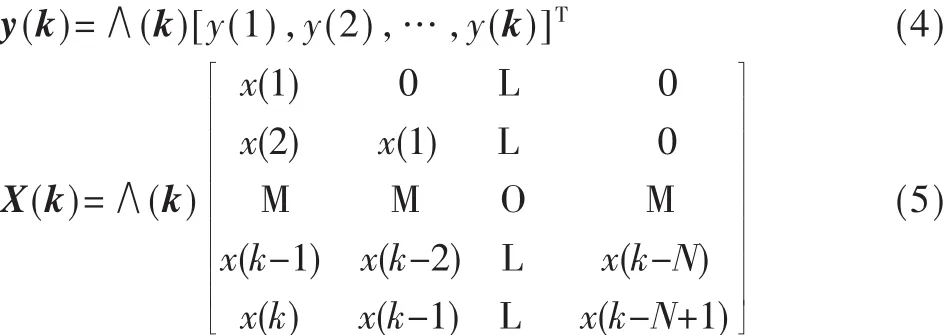
误差向量 ε(k)=y(k)-X(k)w(k)，因此代价函数可表示为：

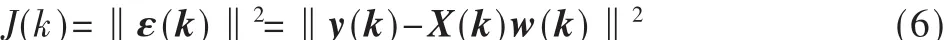
根据矩阵的QR分解定理，存在一个k×k维正交矩阵 Q(k)使得：

式中，R(k)表示一个 N×N维的上三角矩阵，有时也称为Cholesky因子；0表示一个(k-N)×N维的零矩阵，对加权期望输出信号向量y(k)进行相同的正交变换，可以得到：

式中，z(k)为 N×1 维向量，v(k)为(k-N)×1 维向量。由于正交变换不改变向量的范数，则代价函数可以重写为：

把式(7)、式(8)代入式(9)，可以得到：

从式(10)可以看出，当右面向量中顶部的 N×1维向量等于零向量时，代价函数取最小值，这等价于R(k)·w(k)=z(k)，则 w(k)=R-1(k)z(k) (11)

如果能够直接更新矩阵R-1(k)，就可以直接计算权系数向量，矩阵R-1(k)被称为逆Cholesky因子。假设已知R-1(k-1)和 z(k-1)，如果能够用递推方式计算 R-1(k)和 z(k)，就可以递推计算权系数向量。

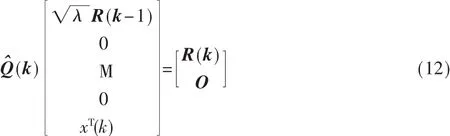
式中，A 为一 N×N 维方阵，δ=γ(k)，得：

把式(16)、式(17)代入式(11)可得到：

定义一个N×1维状态向量d(k)如下：

因此向量c可以重写为：c=-δd(k)

因此w(k)迭代公式为：

式中，e(k)=y(k)-xT(k)w(k-1)，表示自适应滤波器的先验估计误差。

从式(23)可以看出，只要求得增益向量g(k)和标量就可以更新权系数向量w(k)。根据定义，这两个未知量由状态向量d(k)决定，而d(k)由逆 Cholesky因子R-1(k-1)计算得到。所以，未知量都可以由R-1(k-1)计算得到。

R-1(k-1)满足下面方程：

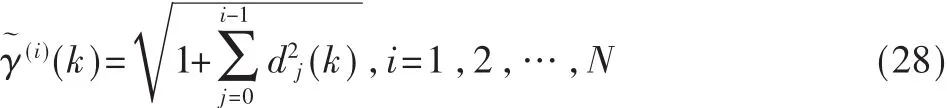
因此，角度参数函数的计算公式为：

从以上的算法推断可知，基于逆QR分解的递推最小二乘法(IQRD-RLS)的运算总量是7N(N+1)/2+3N+1，而除法和平方根运算次数是3N+1次。

2 IQRD-RLS[6]算法在扩频系统中的应用仿真研究

直接序列扩频通信系统通常包括信道编码器、译码器、调制器、解调器以及两个完全一致的伪随机序列发生器，其中，一个在发送端与调制器相接，另一个在接收端与解调器相接。而扩频是通过伪噪声序列(PN)对发送的信息数据进行调制来实现的。在接收端，原伪噪声序列和所收信号的互相关运算可将窄带干扰扩展到DS信号的整个频带，使干扰等效为幅度较低、频谱较平坦的噪声；同时，将DS信号解扩，恢复原始信息数据。由于窄带干扰是非高斯的，样值间有很强的相关性，可以从过去样值来估计当前样值。而DS信号频谱平坦，以Chips率取样的样值之间几乎不相关，所以解扩前利用自适应滤波算法对信号滤波，从当前信号中减去干扰估值，再将差信号与PN码进行相关解扩，可大大提高直扩通信系统的性能。

为了检验基于IQRD-RLS自适应均衡算法在DSSS扩频系统的抗干扰、降低接收信号错误率的性能，本文考虑如下系统功能的信道：从QPSK星座获得的符号用来训练一个自适应滤波器，自适应滤波器的系数采用直接决定模式下从16-QAM调制星座获得的500个符号。信噪比设置为30 dB、自适应滤波器系数为35。在训练模式下，使用的算法是 LMS(μ=0.001)、NLMS(μ=0.4)和IQRD-RLS(λ=0.99)。结果将显示为散射图的输出信号，该情况下不同数目的训练符号为 150、300和600，仿真结果如图1所示。

图1 仿真结果

从图1可以看出，IQRD-RLS、LMS和 NLMS三种算法随着训练符号的增加，均不同程度上降低了接收信号的错误率，提高了接收端接收信号的可靠性，极大地改善了通信质量，特别是IQRD-RLS算法效果更佳。

本文详细地分析了基于逆QR分解的IQRD-RLS自适应均衡算法在DS-SS系统中的应用。该算法有效降低了计算复杂度和接收信号的错误率，改善了矩阵条件数，提高了通信质量，具有比基于相关矩阵的最小二乘算法更好的数值稳定性。本算法还有很多有待改进的地方，进一步的工作就是继续分析那些更好的算法，以不断完善系统模型，以期更好地应用于实践中。

[1]西蒙赫金.自适应滤波器原理[M].第 4版.郑宝玉，译.北京：电子工业出版社，2004.

[2]LIU Z S，LI J.A QR-based least mean squares algorithm for adaptive parameter estimation[J].IEEE Transactions on Circuits and Systems-II： Analog and Digital Signal Processing， 1988，45：321-329.

[3]洪增.矩阵理论与方法[M].北京：电子工业出版社，2006.

[4]藏珍，徐向东.一种基于最小二乘的DS-SS系统搞窄带干扰方法[J].空军雷达学院报，2006，20(3)：174-176，179.

[5]姜波，杨军，张尔扬.稀疏自适应 Volterra滤波的 QRD-RLS 算法[J].信号处理，2008，24(4).

[6]冯地耘，陈立万.基于 LCMV的 IQRD-SMI自适应数字波束形成算法[J].兰州理工大学学报，2007，33(1).